题目要求

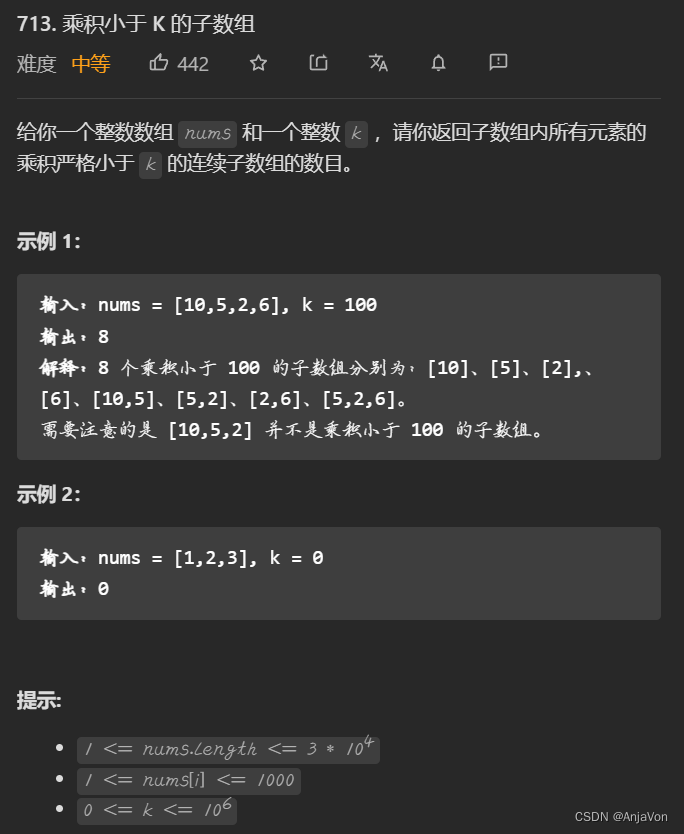
在这里插入图片描述

思路一：前缀和+二分查找

乘积想搞成前缀和就搞对数，所以预处理一个对数前缀和数组 $l o g P r e$ ；
然后依次固定右端点 $r i g h t$ ，二分找合法的左端点 $l e f t$ ：
- 即满足 $logPre[right+1]-logPre[left]<\log k$ ，也就是左端点满足 $logPre[left]>logPre[right+1]-\log k$ ；
- 为了保证精度，避免数值相等却被误判，要加个 $10^{-10}$ 。

Java

class Solution {
    public int numSubarrayProductLessThanK(int[] nums, int k) {
        if(k <= 1)
            return 0;
        int n = nums.length, res = 0;
        double[] logPre = new double[n + 1];
        for(int i = 0; i < n; i++)
            logPre[i + 1] = logPre[i] + Math.log(nums[i]);

        double logk = Math.log(k);
        for(int right = 0; right < n; right++) {
            int l = 0, r = right +  1;
            int left = right + 1;
            double tmp = logPre[right + 1] - logk + 1e-10;
            while(l <= r) {
                int m = (l + r) / 2;
                if(logPre[m] > tmp) { 
                    left = m;
                    r = m - 1;
                }
                else
                    l = m + 1;
            }
            res += right - left + 1;
        }
        return res;
    }
}

时间复杂度： $O(n\log n)$ ，预处理前缀和复杂度为 $O (n)$ ，二分查找复杂度为 $O(\log n)$ ，固定右端点 $n$ 次共 $O(n\log n)$
空间复杂度： $O (n)$ ，存放前缀和

C++

class Solution {
public:
    int numSubarrayProductLessThanK(vector<int>& nums, int k) {
        if(k <= 1)
            return 0;
        int n = nums.size(), res = 0;
        double logPre[n + 1];
        for(int i = 0; i < n; i++)
            logPre[i + 1] = logPre[i] + log(nums[i]);

        double logk = log(k);
        for(int right = 0; right < n; right++) {
            int l = 0, r = right +  1;
            int left = right + 1;
            double tmp = logPre[right + 1] - logk + 1e-10;
            while(l <= r) {
                int m = (l + r) / 2;
                if(logPre[m] > tmp) { 
                    left = m;
                    r = m - 1;
                }
                else
                    l = m + 1;
            }
            res += right - left + 1;
        }
        return res;
    }
};

时间复杂度： $O(n\log n)$ ，预处理前缀和复杂度为 $O (n)$ ，二分查找复杂度为 $O(\log n)$ ，固定右端点 $n$ 次共 $O(n\log n)$
空间复杂度： $O (n)$ ，存放前缀和

思路二：滑动窗口

固定窗口右端点 $r$ ，找合法的最左端点 $l$ ，然后计算可以构成的连续子串数量，即 $r ? l + 1$ 。

Java

class Solution {
    public int numSubarrayProductLessThanK(int[] nums, int k) {
        int n = nums.length, res = 0;
        if(k <= 1)
            return 0;
        for(int l = 0, r = 0, prod = 1; r < n; r++) {
            prod *= nums[r]; // 当前滑动窗口内元素乘积
            while(prod >= k) // 超了
                prod /= nums[l++]; // 缩小范围
            res += r - l + 1; // 可构成的子串数量
        }
        return res;
    }
}

时间复杂度： $O (n)$ ，右端点遍历数组一遍
空间复杂度： $O (1)$

C++

class Solution {
public:
    int numSubarrayProductLessThanK(vector<int>& nums, int k) {
        int n = nums.size(), res = 0;
        if(k <= 1)
            return 0;
        for(int l = 0, r = 0, prod = 1; r < n; r++) {
            prod *= nums[r]; // 当前滑动窗口内元素乘积
            while(prod >= k) // 超了
                prod /= nums[l++]; // 缩小范围
            res += r - l + 1; // 可构成的子串数量
        }
        return res;
    }
};

时间复杂度： $O (n)$ ，右端点遍历数组一遍
空间复杂度： $O (1)$

Rust

impl Solution {
    pub fn num_subarray_product_less_than_k(nums: Vec<i32>, k: i32) -> i32 {
        (0..nums.len()).fold((0, 1, 0), |(mut l, mut prod, res), r| {
            prod *= nums[r]; // 当前滑动窗口内元素乘积
            while l <= r && prod >= k { // 超了
                prod /= nums[l];
                l += 1;  // 缩小范围
            }
            (l, prod, res + (r - l) as i32 + 1)  // 可构成的子串数量
        }).2
    }
}