

本题涉及到的 前置知识 有:并查集、乘法逆元,如果有不了解的知识点可以看看这两篇之前写的博客。
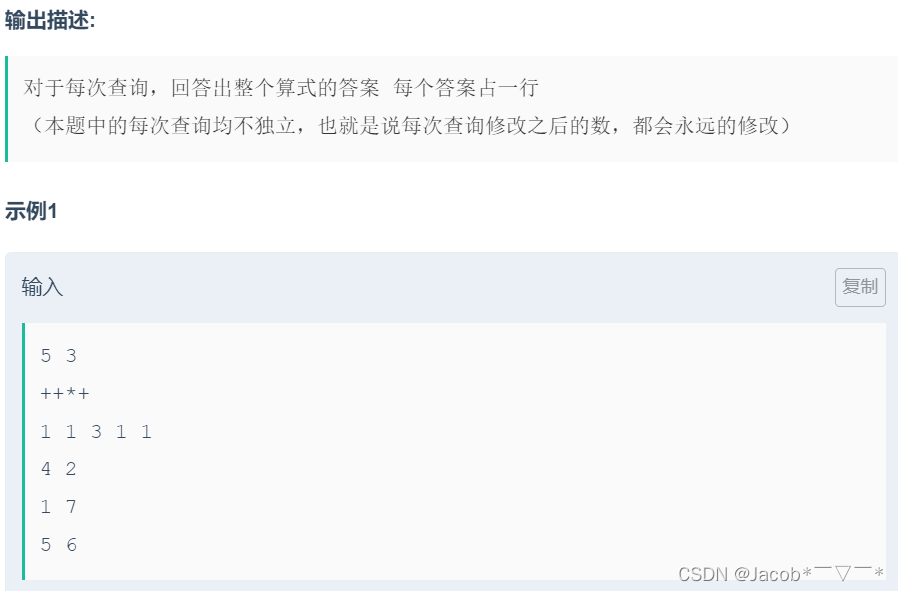
题意:
给定 一串 长度为 n - 1 的运算符号字符串 op[] 和 一串 长度为 n 的整数序列 num[],前者中的元素 对应着 后者两两元素之间 的 运算方式,且 仅仅包含 ’ + ’ 和 ’ * ’ 两个元素。
之后 给出 q 条询问,每次询问代表:将整数序列中的 第 x 个元素改为 y(每次修改后的元素,都会永远的修改),每次询问 都要 输出当前表达式的答案。
思路:
根据题目意思,我们不难发现:
根据 ’ + ’ 可以将整个序列分割成若干个序列集合,且在各个集合的内部有 k 个 ’ * '(k >= 0)。
对于 每个集合,我们 以下标最小的元素 作为 该集合的根节点 root,同时 用 pro[root] 维护 该集合中所有元素的累乘,
显然 表达式的值 sum 即为 所有集合的 pro[root] 总和。
当然,在 还未进行修改查询 时,我们要 将 pro 数组 和 sum 初始值 预处理。
-
对于
pro数组,可以在 合并集合 的时候进行计算(基本的累乘),此外,对于合并集合,显然当 两个整数之间运算符为 ’ * ’ 且 不属于同一个集合 时,可以将 运算符 ’ * ’ 前后 两个整数序列中的元素 进行合并(将 下标较大者 合并至 下标较小者 的集合 中)。 -
对于
sum初始值,将 所有集合的pro[root]累加 即为答案。
之后开始 q 条 修改查询,在每一条询问中:
- 我们要 先找到
num序列中第x个元素 从属 哪个集合,计算出 该元素的改变会对整个集合的pro[root]造成的变化值change,显然输出答案为sum + change。
注意的细节:
- 关于本题的 输入,我是将 运算符的下标 设置为 奇数,将 整数的下标 设置为 偶数。(因此,在后续 修改查询 的时候我们需要 用
get函数将x转化成 下标,即:get函数 返回num中的第x个元素 对应的 下标) - 修改查询时,应该 将所有应该修改的地方都要修改,比如
pro数组,num数组,不能遗漏。 - 由于本题涉及到了 在
mod下进行除法运算,因此一定要 “将 除一个数 转化成 乘一个数的逆元”,此外,为了 防止取模结果为负,应该 先加mod后 模mod,这两条是这类 取模题 的 常见套路,必须牢记。
具体可见代码和注释。
时间复杂度:
O
(
q
l
o
g
(
m
o
d
)
)
O(qlog(mod))
O(qlog(mod))(q <= 1e5,mod = 1e9+7,主要是 求逆元占用的时间复杂度)
代码:(详细注释)
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e6+10, mod = 1e9+7;
int n, q;
char op[N];
int num[N];
int pro[N];
int p[N];
int Find(int x)
{
if(p[x]!=x) p[x] = Find(p[x]);
return p[x];
}
int qmi(int a, int b) //快速幂,本题用于求逆元
{
int res = 1;
while(b)
{
if(b&1) res = res * a % mod;
b >>= 1;
a = a * a % mod;
}
return res;
}
int get(int x) { return x + (x - 1); } //返回 num 中的第 x 个元素 对应的下标
signed main()
{
scanf("%lld%lld", &n, &q);
getchar(); //一定要加这句
//输入n - 1 个运算符,下标设为偶数,从 2 开始,
int t = n - 1, idx = 2;
while(t--)
{
scanf("%c", &op[idx]);
idx += 2;
}
//输入长度为 n 的整数序列,下标设为奇数,从 1 开始
for(int i=1; i<=idx; i+=2)
{
p[i] = i; //并查集初始化
scanf("%lld", &num[i]);
pro[i] = num[i]; //显然 pro[i] 初始就是 num[i]
}
for(int i=2; i<=idx-2; i+=2)
{
if(op[i]=='*') //当运算符为 * 时开始合并集合
{
int a = Find(i-1), b = Find(i+1); //找到 op[i] 前后两元素所属的集合编号 a、b
if(a!=b)
{
p[b] = a; //将 b 代表集合 合并至 a 代表集合
pro[a] = pro[a] * num[i+1] % mod; //根据 pro 数组的定义,累乘取模计算 pro[a]
}
}
}
//累加计算尚未修改查询时的表达式答案 sum
int sum = 0;
for(int i=1; i<=idx; i+=2)
{
if(p[i]==i) sum = (sum + pro[i]) % mod;
}
//开始查询
while(q--)
{
int x, v; scanf("%lld%lld", &x, &v);
//因为上面我们均是将下标进行操作,因此这里需要用 get(x) 转化一下
//get(x) 表示 num 中的第 x 个元素 对应的下标
int aa = Find(get(x));
int &t = num[get(x)];
int change = pro[aa] * qmi(t, mod-2) % mod * v % mod - pro[aa]; //计算更改元素造成的影响值,注意用逆元
//该更改的都要更改
pro[aa] = pro[aa] * qmi(t, mod-2) % mod * v % mod;
t = v;
//更新答案 sum,输出
sum = (sum + change + mod) % mod; //为了防止取模结果为负,应该先加mod后模mod(这是一个常见套路)
printf("%lld\n", sum);
}
return 0;
}
