一、树的概念
这是一颗大自然的树

这是数据结构中的树
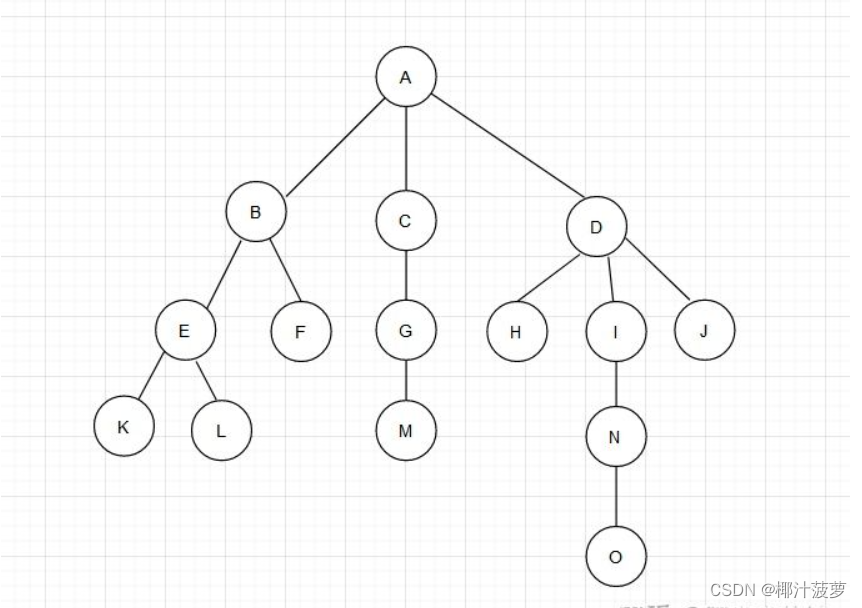
二者看起来是如此的相像,现实中的树是根在地上,枝干往上长,叶子在整颗树的最顶端。而数据结构中的树如此相似却又刚好相反,树的根在上面,枝干往下长,叶子在树的最底端。先在脑子里有这么个概念,具体有关于树的术语在下文详细提及。
定义
树是一种非线性结构,由n(n >= 0)个结点组成,当n=0的时候,此时的树被称为空树。当n>0时,此时的树存在一个结点被称为根结点(如上图的A结点),而除根结点外的其它结点可以分为m个集合,每个集合本身又是一颗树,被称为根结点的子树。
由定义可以看出,树中结点最多只能有一个父结点,可以有0个或多个子结
分析
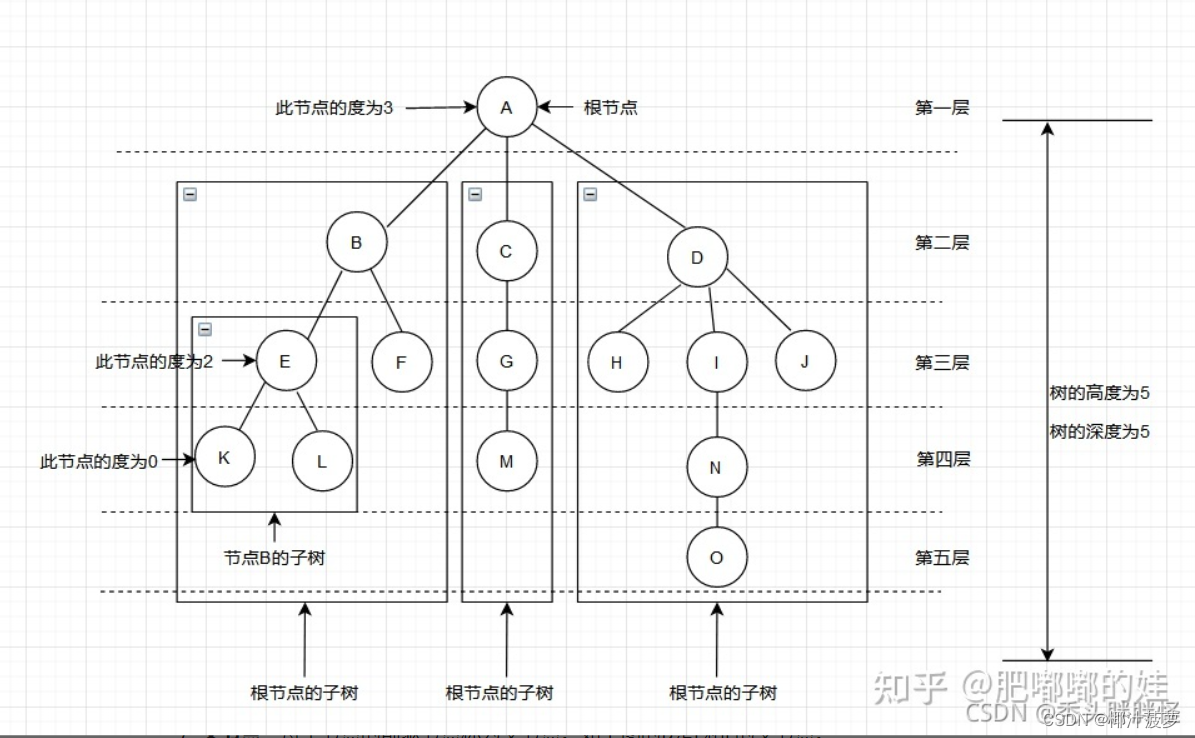
这里即将介绍一些树的术语:
- 树的根结点:一棵树的根结点位于这个树的最上面,它没有父结点。
- 结点的度:一个结点包含子树的数目称为该结点的度。
- 叶子结点:度为0的结点称为叶子结点。
- 结点的层次:从根结点开始,根结点的层次为1,根结点的子结点为第二层,如此往下类推。
- 树的度:树中结点的度的最大值。上图树的度为3.
- 树的高度或深度:树中结点的最大层次。
- 父结点:每个结点的前驱结点称为父结点。如上图的B是E和F的父结点。
- 子结点:每个结点的后继结点称为子结点。如上图的E和F是B的子结点。
- 兄弟结点:同个父结点下的子结点称为兄弟结点。如上图的E和F,K和L。
- 结点的高度:结点距最底层的叶子结点的距离称为结点的高度。如上图B结点的高度为4。
- 结点的深度:结点距根结点的距离称为结点的深度。如上图的B结点的深度为2。
从10和11可以看出一个结点的高度和深度未必相等。但是对于一棵树而言,高度和深度是同一个概念。
二、二叉树
二叉树:所有结点下最多只能有两个子结点,满足该条件即为二叉树;顾名思义,二叉树最多只能有两个分叉;
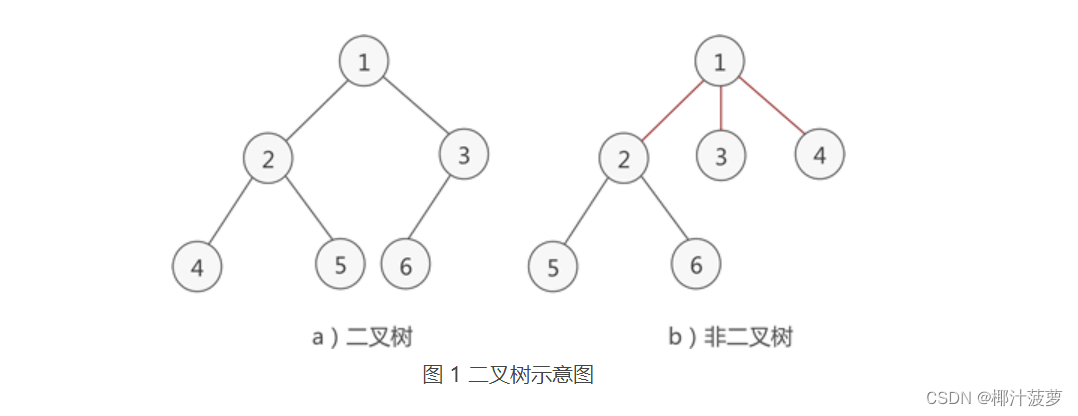
二叉树遍历:
-
先序遍历
父结点–>左子树—>右子树

-
中序遍历
左子树–>父节点–>右子树

-
后序遍历
左子树–>右子树–>父节点

其实很好理解,顺序说的都是父结点的顺序,先序就是先父结点再左右,中序就是父结点总是在中间,后序就是父结点总在最后;子结点都是先左后右
算法代码:
public class TreeNode<T> {
private T val;
private TreeNode<T> left;
private TreeNode<T> right;
public T getVal() {
return val;
}
public void setVal(T val) {
this.val = val;
}
public TreeNode<T> getLeft() {
return left;
}
public void setLeft(TreeNode<T> left) {
this.left = left;
}
public TreeNode<T> getRight() {
return right;
}
public void setRight(TreeNode<T> right) {
this.right = right;
}
//先序
public static <T> void preOrderTraverse(TreeNode<T> tree) {
if(tree==null) return;
System.out.println(tree.getVal());
preOrderTraverse(tree.getLeft());
preOrderTraverse(tree.getRight());
}
//中序
public static <T> void inOrderTraverse(TreeNode<T> tree) {
if(tree==null) return;
preOrderTraverse(tree.getLeft());
System.out.println(tree.getVal());
preOrderTraverse(tree.getRight());
}
//后序
public static <T> void postOrderTraverse(TreeNode<T> tree) {
if(tree==null) return;
preOrderTraverse(tree.getLeft());
preOrderTraverse(tree.getRight());
System.out.println(tree.getVal());
}
}
