[数据结构与算法]树链剖分简介【轻重链剖分】洛谷P3384

模板题：洛谷P3384传送门

树链剖分可以做到 $O(logn)$修改树上两点之间的路径上所有点的值、 查询树上两点之间的路径上节点权值的和/极值（就是线段树能干啥它能干啥）。当然前置知识就是$\text{dfs}$和线段树。

树链剖分有重链剖，长链剖，还有只听过的实链剖（看oiwiki所知，Link/cut Tree所用），一般未特指都是重链剖分。

定义重子节点表示其子节点中子树最大的子结点。多个最大子节点取其中一个作重儿子即可。

轻儿子作为重链顶点，一个轻儿子和多个重儿子（也可能没有）组成一条重链，这样一棵树就被剖成多条重链。

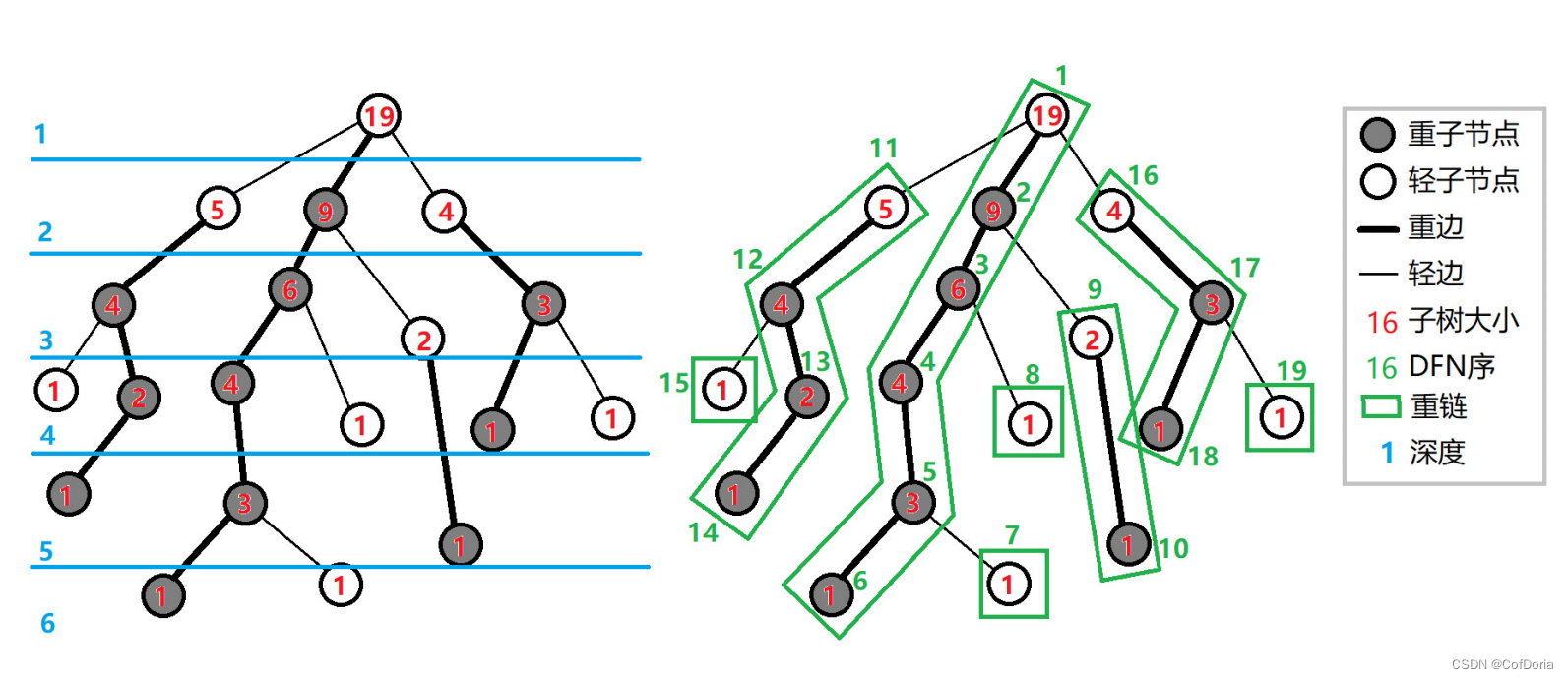
两次dfs，第一次找出各节点重儿子，第二次每个节点优先遍历重儿子，走出的dfs序重，重链的dfs序都是连续的，维护和统计两点之间路径的信息就可以依靠重链和线段树来更新和查询。

对于题目要求的子树信息，在dfs回溯到各节点，表示该节点子树遍历完全，记录一下当前dfs序为该节点子树在dfs序上的区间右端点

Accepted code

#include <iostream>
#include <vector>
#define ll long long
#define maxn 100005
#define dl (d << 1)
#define dr (d << 1 | 1)
using namespace std;

ll n, m, r, p;
ll a[maxn];
//依次是重儿子、子树规模、父节点、dfs序、子树dfs序右端点、深度、所在重链顶点、dfs对应节点编号、dfs个数
ll son[maxn], _size[maxn], fa[maxn], dfn[maxn], edfn[maxn], dep[maxn],
    top[maxn], rk[maxn], tot = 1;
vector<ll> mp[maxn];  //邻接表 各个点的边

struct node {
    ll l, r;
    ll sum, tag;
} sgt[maxn << 2];

void pushup(ll d) { sgt[d].sum = (sgt[dl].sum + sgt[dr].sum) % p; }

void pushdown(ll d) {
    sgt[dl].sum = (sgt[dl].sum + (sgt[dl].r - sgt[dl].l + 1) * sgt[d].tag) % p;
    sgt[dr].sum = (sgt[dr].sum + (sgt[dr].r - sgt[dr].l + 1) * sgt[d].tag) % p;
    sgt[dl].tag = (sgt[dl].tag + sgt[d].tag) % p;
    sgt[dr].tag = (sgt[dr].tag + sgt[d].tag) % p;
    sgt[d].tag = 0;
}

void build(ll d, ll l, ll r) {
    sgt[d].l = l;
    sgt[d].r = r;
    sgt[d].sum = 0;
    sgt[d].tag = 0;
    if (l == r) {
        sgt[d].sum = a[rk[l]] % p;
        return;
    }
    ll mid = l + r >> 1;
    build(dl, l, mid);
    build(dr, mid + 1, r);
    pushup(d);
}

void modify(ll d, ll l, ll r, ll v) {
    if (sgt[d].l >= l && sgt[d].r <= r) {
        sgt[d].sum = (sgt[d].sum + (sgt[d].r - sgt[d].l + 1) * v) % p;
        sgt[d].tag = (sgt[d].tag + v) % p;
        return;
    }
    if (sgt[d].tag) pushdown(d);
    ll mid = sgt[d].l + sgt[d].r >> 1;
    if (l <= mid) modify(dl, l, r, v);
    if (r > mid) modify(dr, l, r, v);
    pushup(d);
}

ll query(ll d, ll l, ll r) {
    if (sgt[d].l >= l && sgt[d].r <= r) return sgt[d].sum % p;
    if (sgt[d].tag) pushdown(d);
    ll mid = sgt[d].l + sgt[d].r >> 1;
    ll ret = 0;
    if (l <= mid) ret += query(dl, l, r);
    if (r > mid) ret += query(dr, l, r);
    return ret % p;
}

ll dfs1(ll u, ll dp, ll f) {
    dep[u] = dp;
    son[u] = 0;
    _size[son[u]] = 0;
    _size[u] = 1;
    for (auto v : mp[u]) {
        if (v == f) continue;
        _size[u] += dfs1(v, dp + 1, u);
        fa[v] = u;
        if (_size[son[u]] < _size[v]) son[u] = v;  //当前规模更大 更新重儿子
    }
    return _size[u];
}

void dfs2(ll u, ll tp) {
    top[u] = tp;  //记录当前重链的顶点
    dfn[u] = tot;
    rk[dfn[u]] = u;
    ++tot;
    if (son[u]) {
        dfs2(son[u], tp);  //重链顶点延续
        for (auto v : mp[u]) {
            if (v == fa[u]) continue;
            if (v == son[u]) continue;
            dfs2(v, v);  //轻链顶点就是自己
        }
    }
    edfn[u] = tot - 1;
}

void add(ll x, ll y, ll z) {
    ll a = x, b = y;
    while (top[a] != top[b]) {
        if (dep[top[a]] < dep[top[b]]) swap(a, b);  //对比top[a]和top[b]的深度
        modify(1, dfn[top[a]], dfn[a], z);
        a = fa[top[a]];  // 起点深度低的链向上转移到前一条链
    }
    if (dep[a] > dep[b]) swap(a, b);
    modify(1, dfn[a], dfn[b], z);
}

// dfn=>dfs序 edfn=>dfs序上子树结束处
void add(ll x, ll z) { modify(1, dfn[x], edfn[x], z); }

ll sum(ll x, ll y) {  //类似前面add
    ll a = x, b = y;
    ll ret = 0;
    while (top[a] != top[b]) {
        if (dep[top[a]] < dep[top[b]]) swap(a, b);
        ret = (ret + query(1, dfn[top[a]], dfn[a])) % p;
        a = fa[top[a]];
    }
    if (dep[a] > dep[b]) swap(a, b);
    ret = (ret + query(1, dfn[a], dfn[b])) % p;
    return ret;
}

ll sum(ll x) { return query(1, dfn[x], edfn[x]); }

ll opt, x, y, z;
int main() {
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    cin >> n >> m >> r >> p;
    for (ll i = 1; i <= n; i++) cin >> a[i];
    for (ll i = 0, u, v; i < n - 1; i++) {
        cin >> u >> v;
        mp[u].push_back(v);
        mp[v].push_back(u);
    }
    dfs1(r, 0, 0);  //求出各节点深度、父亲和重儿子
    dfs2(r, r);  //求各节点所在重链顶点、dfs序和该节点为根子树dfs序右端点
    build(1, 1, n);  //根据dfs序建线段树
    while (m--) {
        cin >> opt;
        if (opt == 1) {
            cin >> x >> y >> z;
            add(x, y, z);  // x y之间都加上z
        } else if (opt == 2) {
            cin >> x >> y;
            cout << sum(x, y) << '\n';  //查询x y路径上的和
        } else if (opt == 3) {
            cin >> x >> z;
            add(x, z);  // x为根节点的子树都加上z
        } else {
            cin >> x;
            cout << sum(x) << '\n';  //查询x为根节点的子树的和
        }
    }
    return 0;
}

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖