
public int[] twoSum(int[] nums, int target) {
int n = nums.length;
for (int i = 0; i < n; i++){
for (int j = i + 1; j < n; j++){
if (nums[i] + nums[j] == target){
return new int[]{i,j};
}
}
}
return new int[0];
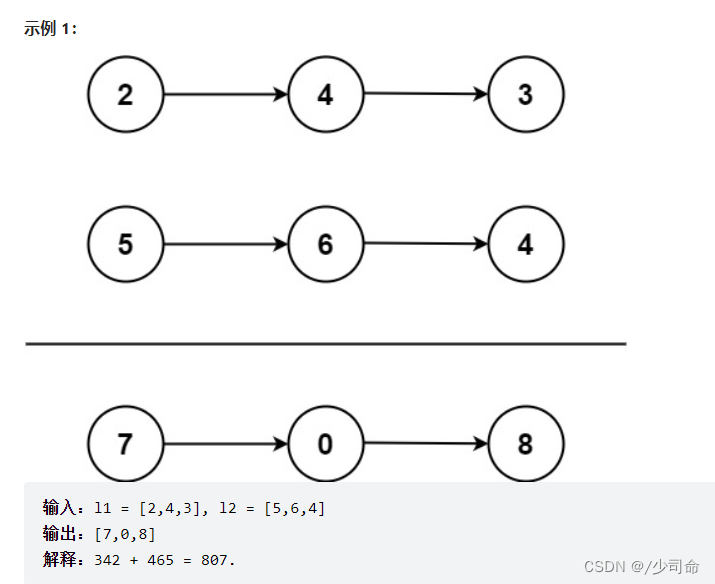
}
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
// 在两条链表上的指针
ListNode p1 = l1, p2 = l2;
// 虚拟头结点(构建新链表时的常用技巧)
ListNode dummy = new ListNode(-1);
// 指针 p 负责构建新链表
ListNode p = dummy;
// 记录进位
int carry = 0;
// 开始执行加法,两条链表走完且没有进位时才能结束循环
while (p1 != null || p2 != null || carry > 0) {
// 先加上上次的进位
int val = carry;
if (p1 != null) {
val += p1.val;
p1 = p1.next;
}
if (p2 != null) {
val += p2.val;
p2 = p2.next;
}
// 处理进位情况
carry = val / 10;
val = val % 10;
// 构建新节点
p.next = new ListNode(val);
p = p.next;
}
// 返回结果链表的头结点(去除虚拟头结点)
return dummy.next;
}
public int lengthOfLongestSubstring(String s) {
if (s.length() == 0){
return 0;
}
HashMap<Character,Integer> map = new HashMap<>();
int max = 0;
int left = 0;
for (int i = 0; i < s.length(); i++){
if (map.containsKey(s.charAt(i))){
left = Math.max(left,map.get(s.charAt(i)) + 1);
}
map.put(s.charAt(i),i);
max = Math.max(max,i - left + 1);
}
return max;
}
public String longestPalindrome(String s) {
String res = "";
for (int i = 0; i < s.length(); i++){
String s1 = palindrom(s,i,i);
String s2 = palindrom(s,i,i+1);
res = res.length() > s1.length()? res : s1;
res = res.length() > s2.length()? res : s2;
}
return res;
}
private String palindrom(String s, int l, int r) {
while (l >=0 && r < s.length() && s.charAt(l) == s.charAt(r)){
l--;
r++;
}
return s.substring(l+1,r);
}
public int maxArea(int[] height) {
int left = 0,right = height.length - 1;
int res = 0;
while (left < right){
int cur = Math.min(height[left],height[right]) * (right - left);
res = Math.max(res,cur);
if (height[left] < height[right]){
left++;
}else {
right--;
}
}
return res;
}
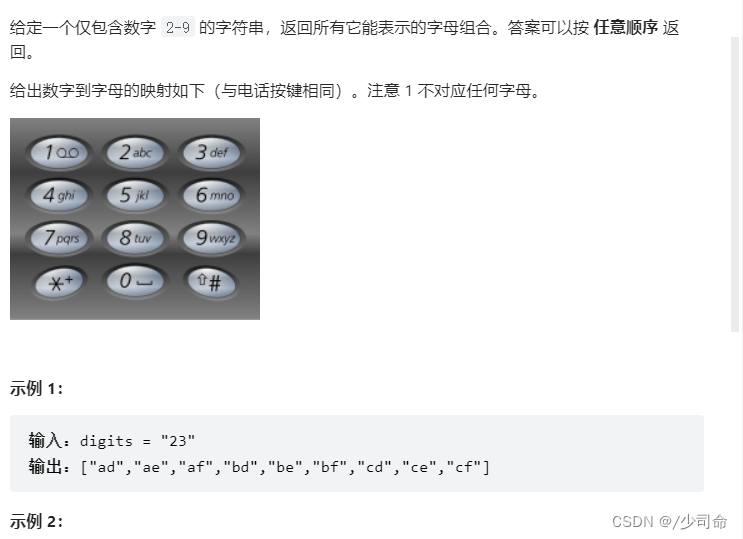
String[] mapping = new String[]{
"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"
};
List<String> res = new LinkedList<>();
public List<String> letterCombinations(String digits) {
if (digits.isEmpty()) {
return res;
}
backtrack(digits, 0, new StringBuilder());
return res;
}
private void backtrack(String digits, int start, StringBuilder sb) {
if (sb.length() == digits.length()){
res.add(sb.toString());
return;
}
for (int i = start; i < digits.length(); i++){
int digit = digits.charAt(i) - '0';
for (char c : mapping[digit].toCharArray()){
sb.append(c);
backtrack(digits,i+1,sb);
sb.deleteCharAt(sb.length()-1);
}
}
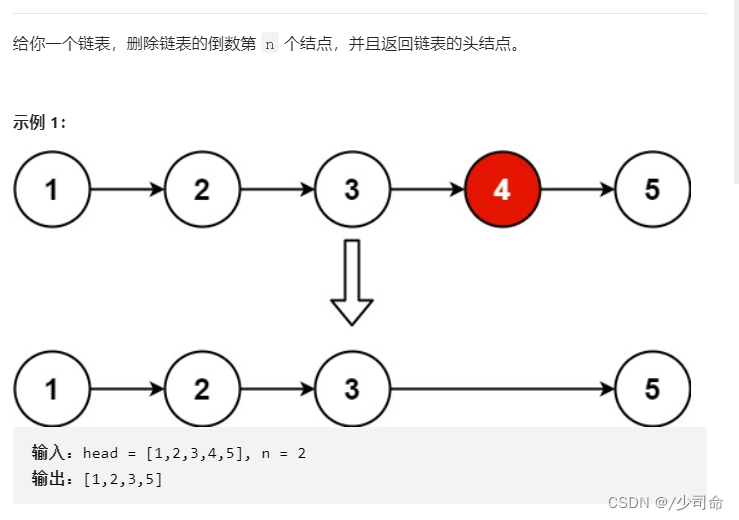
}
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0,head);
Stack<ListNode> stack = new Stack<>();
ListNode cur = dummy;
while (cur != null){
stack.push(cur);
cur = cur.next;
}
for (int i = 0; i < n; i++){
stack.pop();
}
ListNode prev = stack.peek();
prev.next = prev.next.next;
return dummy.next;
}
public boolean isValid(String s) {
if (s.length() ==0 && s == null){
return false;
}
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i ++){
char ch = s.charAt(i);
if(ch == '(' || ch == '{' || ch == '['){
stack.push(ch);
}else {
if (stack.isEmpty()){
return false;
}
char tmp = stack.peek();
if (tmp == '(' && ch == ')' || tmp == '{' && ch == '}' || tmp == '[' && ch == ']'){
stack.pop();
}else {
return false;
}
}
}
if (stack.isEmpty()){
return true;
}else {
return false;
}
}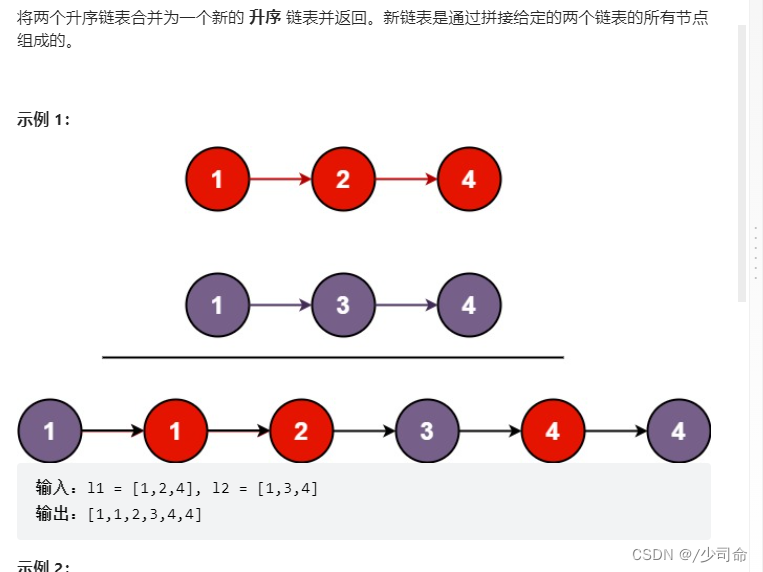
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if (list1 == null){
return list2;
}
if (list2 == null){
return list1;
}
if (list1.val < list2.val){
list1.next = mergeTwoLists(list1.next,list2);
return list1;
}else {
list2.next = mergeTwoLists(list1,list2.next);
return list2;
}
}
public List<String> result = new LinkedList<>();
public List<String> generateParenthesis(int n) {
StringBuffer sb = new StringBuffer();
blackTrack(n,n,result,sb);
return result;
}
private void blackTrack(int left, int right, List<String> result, StringBuffer sb) {
if (left > right){
return;
}
if (left < 0 || right < 0){
return;
}
if (left == 0 && right == 0){
result.add(sb.toString());
}
sb.append("(");
blackTrack(left-1,right,result,sb);
sb.deleteCharAt(sb.length() - 1);
sb.append(")");
blackTrack(left,right-1,result,sb);
sb.deleteCharAt(sb.length()-1);
}
public int longestValidParentheses(String s) {
Stack<Integer> stack = new Stack<>();
int[] dp = new int[s.length()+1];
for (int i = 0; i < s.length(); i++){
if (s.charAt(i) == '('){
stack.push(i);
dp[i+1] = 0;
}else {
if (!stack.isEmpty()){
int leftIndex = stack.pop();
int len = 1 + i - leftIndex + dp[leftIndex];
dp[i+1] = len;
}else {
dp[i+1] = 0;
}
}
}
int res = 0;
for (int i = 0; i < dp.length; i++){
res = Math.max(res,dp[i]);
}
return res;
}?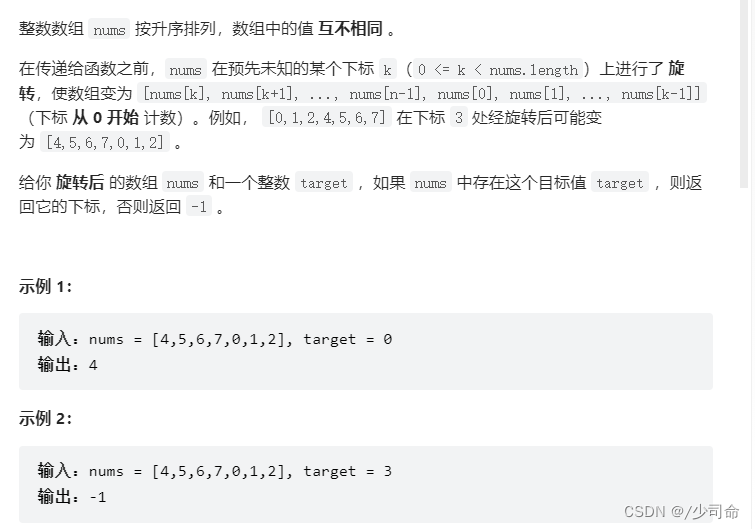
public int search(int[] nums, int target) {
int n = nums.length;
if (n == 0){
return -1;
}
if (n == 1){
return nums[0] == target ? 0 : -1;
}
int l = 0, r = n - 1;
while (l <= r){
int mid = (l + r) / 2;
if (nums[mid] == target){
return mid;
}
if (nums[0] <= nums[mid]){
if (nums[0] <= target && target < nums[mid]){
r = mid - 1;
}else {
l = mid + 1;
}
}else {
if (nums[mid] < target && target <= nums[n - 1]){
l = mid + 1;
}else {
r = mid - 1;
}
}
}
return -1;
}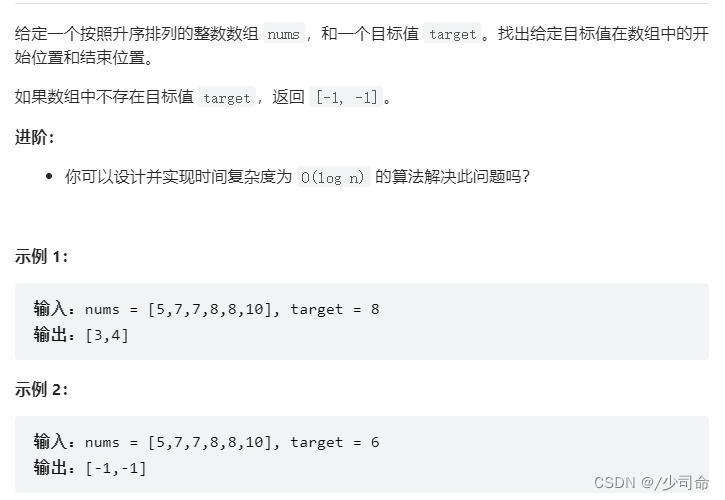
public int[] searchRange(int[] nums, int target) {
return new int[]{left_num(nums,target),right_num(nums,target)};
}
private int right_num(int[] nums, int target) {
int left = 0, right = nums.length-1;
while (left <= right){
int mid = left + (right - left) / 2;
if (nums[mid] < target){
left = mid + 1;
}else if (nums[mid] > target){
right = mid - 1;
}else if(nums[mid] == target){
left = mid + 1;
}
}
if (right < 0 || nums[right] != target){
return -1;
}
return right;
}
private int left_num(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right){
int mid = left + (right - left) / 2;
if (nums[mid] < target){
left = mid + 1;
}else if (nums[mid] > target){
right = mid - 1;
}else if (nums[mid] == target){
right = mid - 1;
}
}
if (left >= nums.length || nums[left] != target){
return -1;
}
return left;
}?
List<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> track = new LinkedList<>();
int trackSum = 0;
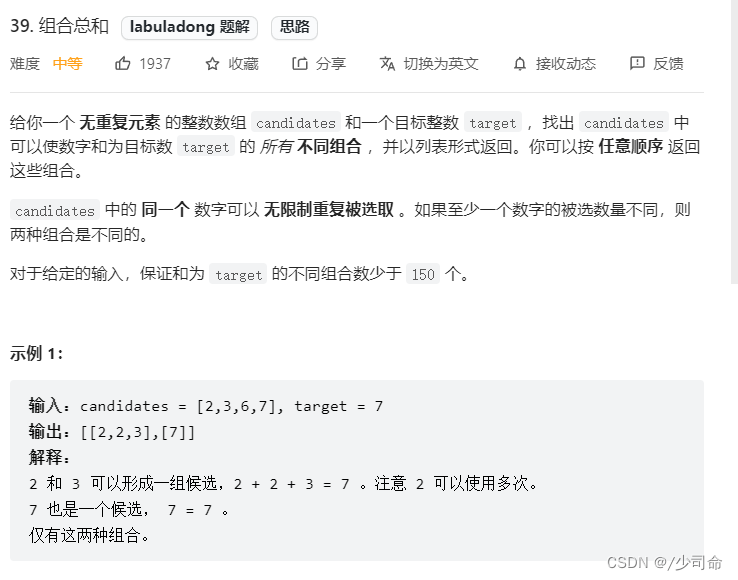
public List<List<Integer>> combinationSum(int[] candidates, int target) {
if (candidates.length == 0){
return res;
}
backtrack(candidates,0,target);
return res;
}
private void backtrack(int[] candidates, int start, int target) {
if (trackSum == target){
res.add(new LinkedList<>(track));
return;
}
if (trackSum > target){
return;
}
for (int i = start; i < candidates.length; i++){
trackSum += candidates[i];
track.add(candidates[i]);
backtrack(candidates,i,target);
trackSum-=candidates[i];
track.removeLast();
}
}
public int trap(int[] height) {
if (height.length == 0){
return 0;
}
int n = height.length;
int res = 0;
int[] L_max = new int[n];
int[] R_max = new int[n];
L_max[0] = height[0];
R_max[n-1] = height[n-1];
for (int i = 1; i < n; i++){
L_max[i] = Math.max(height[i],L_max[i-1]);
}
for (int i = n - 2; i >= 0; i--){
R_max[i] = Math.max(height[i],R_max[i+1]);
}
for (int i = 1; i < n -1; i++){
res += Math.min(L_max[i],R_max[i]) - height[i];
}
return res;
}
List<List<Integer>> res = new LinkedList<>();
LinkedList track = new LinkedList<>();
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
used = new boolean[nums.length];
backtrack(nums);
return res;
}
private void backtrack(int[] nums) {
if (track.size() == nums.length){
res.add(new LinkedList<>(track));
return;
}
for (int i = 0; i < nums.length; i++){
if (used[i]){
continue;
}
used[i] = true;
track.addLast(nums[i]);
backtrack(nums);
track.removeLast();
used[i] = false;
}
}
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n; i++){
for (int j = i; j < n; j++){
int tmp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = tmp;
}
}
for (int[] row : matrix){
reverse(row);
}
}
public void reverse(int[] arr){
int i = 0, j = arr.length - 1;
while (i < j){
int tmp= arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
}
public List<List<String>> groupAnagrams(String[] strs) {
HashMap<String,List<String>> codeToGroup = new HashMap<>();
for (String s : strs){
String code = encodes(s);
codeToGroup.putIfAbsent(code,new LinkedList<>());
codeToGroup.get(code).add(s);
}
List<List<String>> res = new LinkedList<>();
for (List<String> group: codeToGroup.values()){
res.add(group);
}
return res;
}
private String encodes(String s) {
char[] code = new char[26];
for (char c : s.toCharArray()){
int data = c - 'a';
code[data]++;
}
return new String(code);
}
public int maxSubArray(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
dp[0] = nums[0];
if (n == 0){
return 0;
}
for (int i = 1; i < n; i++){
dp[i] = Math.max(nums[i],nums[i] + dp[i-1]);
}
int res = Integer.MIN_VALUE;
for (int i = 0; i < n; i++){
res = Math.max(res,dp[i]);
}
return res;
}?
public boolean canJump(int[] nums) {
int n = nums.length;
int farthest = 0;
for (int i =0; i < n - 1; i++){
farthest = Math.max(i+nums[i],farthest);
if(farthest <= i){
return false;
}
}
return farthest >= n - 1;
}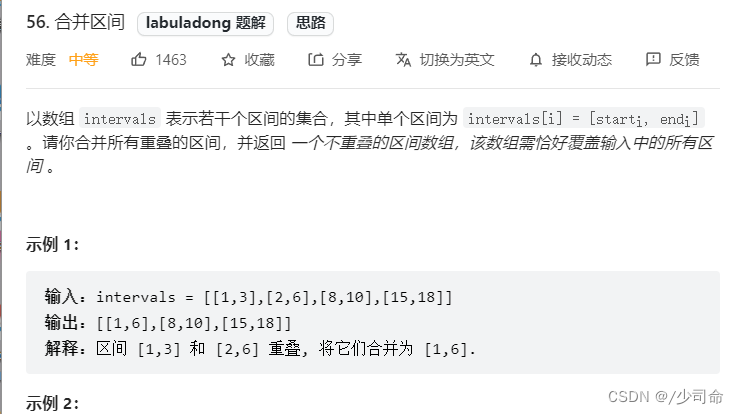
public int[][] merge(int[][] intervals) {
LinkedList<int[]> res = new LinkedList<>();
Arrays.sort(intervals,(a,b) -> {
return a[0] - b[0];
});
res.add(intervals[0]);
for (int i = 1; i < intervals.length; i++){
int[] cur = intervals[i];
int[] last = res.getLast();
if (cur[0] <= last[1]){
last[1] = Math.max(last[1],cur[1]);
}else {
res.add(cur);
}
}
return res.toArray(new int[0][0]);
}
// 备忘录
int[][] memo;
public int uniquePaths(int m, int n) {
memo = new int[m][n];
return dp(m - 1, n - 1);
}
// 定义:从 (0, 0) 到 (x, y) 有 dp(x, y) 条路径
int dp(int x, int y) {
// base case
if (x == 0 && y == 0) {
return 1;
}
if (x < 0 || y < 0) {
return 0;
}
// 避免冗余计算
if (memo[x][y] > 0) {
return memo[x][y];
}
// 状态转移方程:
// 到达 (x, y) 的路径数等于到达 (x - 1, y) 和 (x, y - 1) 路径数之和
memo[x][y] = dp(x - 1, y) + dp(x, y - 1);
return memo[x][y];
}?
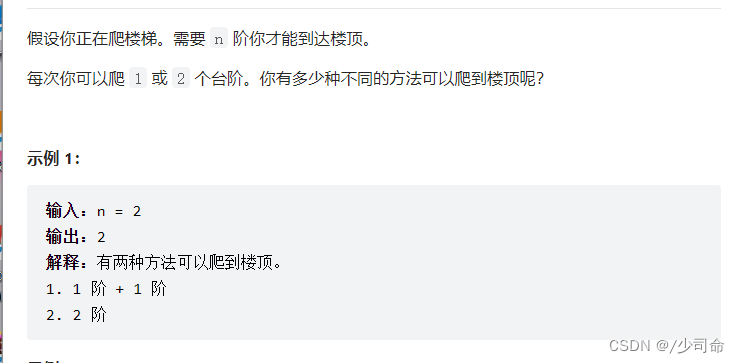
int[][] dp;
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
dp = new int[m][n];
for (int[] row : dp){
Arrays.fill(row,-1);
}
return help(grid,m - 1, n - 1);
}
private int help(int[][] grid, int i, int j) {
if (i == 0 && j == 0){
return grid[0][0];
}
if (i < 0 || j < 0){
return Integer.MAX_VALUE;
}
if (dp[i][j] != -1){
return dp[i][j];
}
dp[i][j] = Math.min(help(grid,i-1,j),help(grid,i,j-1)) + grid[i][j];
return dp[i][j];
}
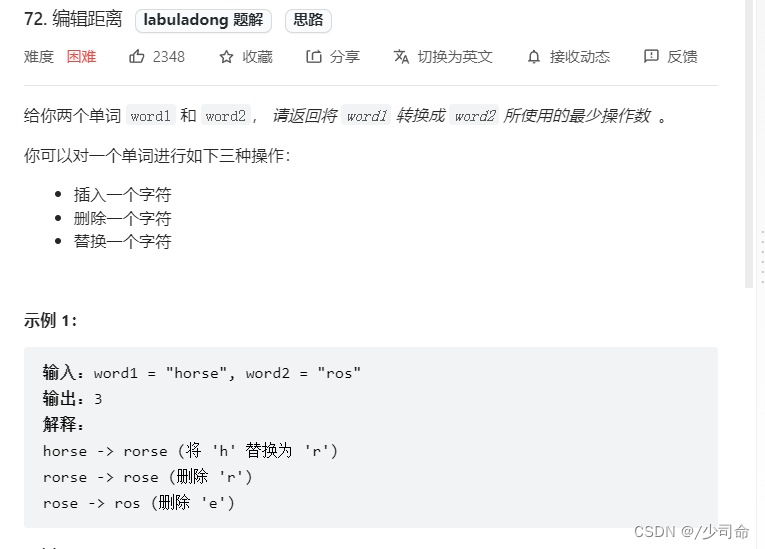
// 备忘录
int[] memo;
public int climbStairs(int n) {
memo = new int[n + 1];
return dp(n);
}
// 定义:爬到第 n 级台阶的方法个数为 dp(n)
int dp(int n) {
// base case
if (n <= 2) {
return n;
}
if (memo[n] > 0) {
return memo[n];
}
// 状态转移方程:
// 爬到第 n 级台阶的方法个数等于爬到 n - 1 的方法个数和爬到 n - 2 的方法个数之和。
memo[n] = dp(n - 1) + dp(n - 2);
return memo[n];
}
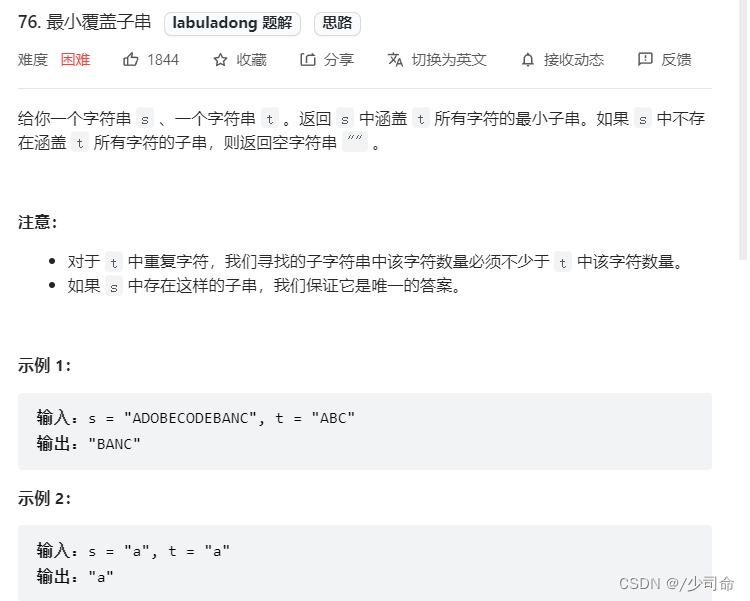
public int minDistance(String s1, String s2) {
int m = s1.length(),n = s2.length();
int[][] dp = new int[m+1][n+1];
for (int i = 1; i <= m; i++)
dp[i][0] = i;
for (int j = 1; j <= n; j++)
dp[0][j] = j;
for (int i = 1; i <= m ;i++){
for (int j = 1; j <= n; j++){
if (s1.charAt(i -1) == s2.charAt(j - 1)){
dp[i][j] = dp[i-1][j-1];
}else {
dp[i][j] = min(
dp[i-1][j] + 1,
dp[i][j-1] + 1,
dp[i-1][j-1] + 1
);
}
}
}
return dp[m][n];
}
int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
public void sortColors(int[] nums) {
int n = nums.length;
int p0 = 0, p2 = n - 1;
for (int i = 0; i <= p2; i++){
while (i <= p2 && nums[i] == 2){
int tmp = nums[i];
nums[i] = nums[p2];
nums[p2] = tmp;
--p2;
}
if (nums[i] == 0){
int tmp = nums[i];
nums[i] = nums[p0];
nums[p0] = tmp;
++p0;
}
}
}?
public String minWindow(String s, String t) {
HashMap<Character,Integer> window_map = new HashMap<>();
HashMap<Character,Integer> t_map = new HashMap<>();
for (int i = 0; i < t.length(); i++){
char c1 = t.charAt(i);
t_map.put(c1,t_map.getOrDefault(c1,0)+1);
}
int left = 0;
int right = 0;
int count = 0;
int len = Integer.MAX_VALUE;
int start = 0;
while (right < s.length()) {
char c = s.charAt(right);
right++;
if (t_map.containsKey(c)) {
window_map.put(c, window_map.getOrDefault(c, 0) + 1);
if (window_map.get(c).equals(t_map.get(c))) {
count++;
}
}
while (count == t_map.size()) {
if (right - left < len) {
start = left;
len = right - left;
}
char d = s.charAt(left);
left++;
if (t_map.containsKey(d)) {
if (window_map.get(d).equals(t_map.get(d))) {
count--;
}
window_map.put(d, window_map.get(d) - 1);
}
}
}
return len == Integer.MAX_VALUE ? "" : s.substring(start,start+len);
}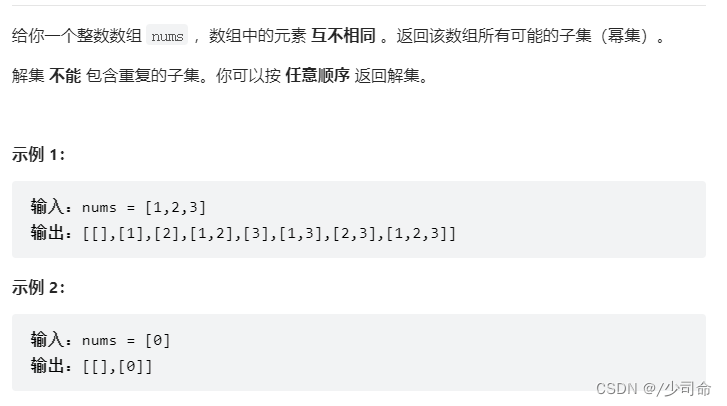
List<List<Integer>> res = new LinkedList<>();
//记录路径
LinkedList<Integer> track = new LinkedList<>();
public List<List<Integer>> subsets(int[] nums) {
backtrack(nums,0);
return res;
}
private void backtrack(int[] nums, int start) {
res.add(new LinkedList<>(track));
for (int i = start; i < nums.length; i++){
track.addLast(nums[i]);
backtrack(nums,i+1);
track.removeLast();
}
}
private static final int[][] BLOCK = {{-1,0},{0,-1},{0,1},{1,0}};
private int rows;
private int cols;
private int len;
private boolean[][] visited;
private char[] charArray;
private char[][] board;
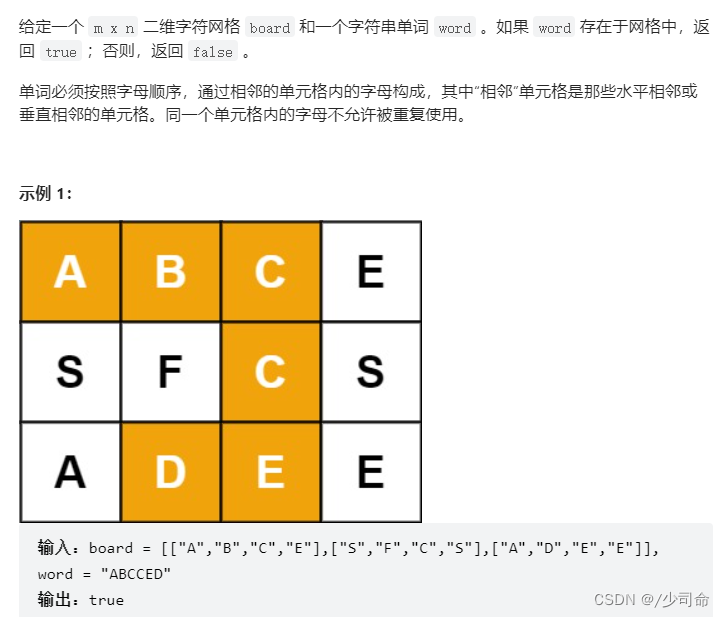
public boolean exist(char[][] board, String word) {
rows = board.length;
if (rows == 0){
return false;
}
cols = board[0].length;
len = word.length();
visited = new boolean[rows][cols];
charArray = word.toCharArray();
this.board = board;
for (int i = 0; i < rows; i++){
for (int j = 0; j < cols; j++){
if (dfs(i,j,0)){
return true;
}
}
}
return false;
}
private boolean dfs(int x, int y, int begin) {
if (begin == len - 1){
return board[x][y] == charArray[begin];
}
if (board[x][y] == charArray[begin]){
visited[x][y] = true;
for (int[] direction : BLOCK){
int newX = x + direction[0];
int newY = y + direction[1];
if (inArea(newX,newY) && !visited[newX][newY]){
if (dfs(newX,newY,begin+1)){
return true;
}
}
}
visited[x][y] = false;
}
return false;
}
private boolean inArea(int x, int y) {
return x >= 0 && x < rows && y >= 0 && y < cols;
}
LinkedList<Integer> list = new LinkedList<>();
public List<Integer> inorderTraversal(TreeNode root) {
traverse(root);
return list;
}
private void traverse(TreeNode root) {
if (root == null){
return;
}
traverse(root.left);
list.add(root.val);
traverse(root.right);
}
int[][] memo;
int numTrees(int n){
memo = new int[n+1][n+1];
return count(1,n);
}
private int count(int lo, int hi) {
if (lo > hi){
return 1;
}
if (memo[lo][hi] != 0){
return memo[lo][hi];
}
int res = 0;
for (int i = lo; i <= hi; i++){
int left = count(lo,i-1);
int right = count(i+1,hi);
res += left*right;
}
memo[lo][hi] = res;
return res;
}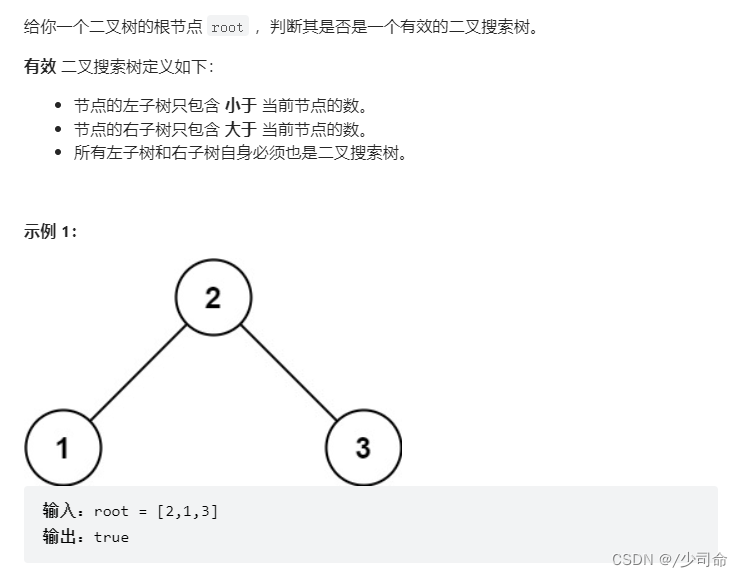
public boolean isValidBST(TreeNode root) {
return isValidBST(root, null, null);
}
/* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
if (root == null){
return true;
}
if (min != null && root.val <= min.val){
return false;
}
if (max != null && root.val >= max.val){
return false;
}
return isValidBST(root.left,min,root) && isValidBST(root.right,root,max);
}
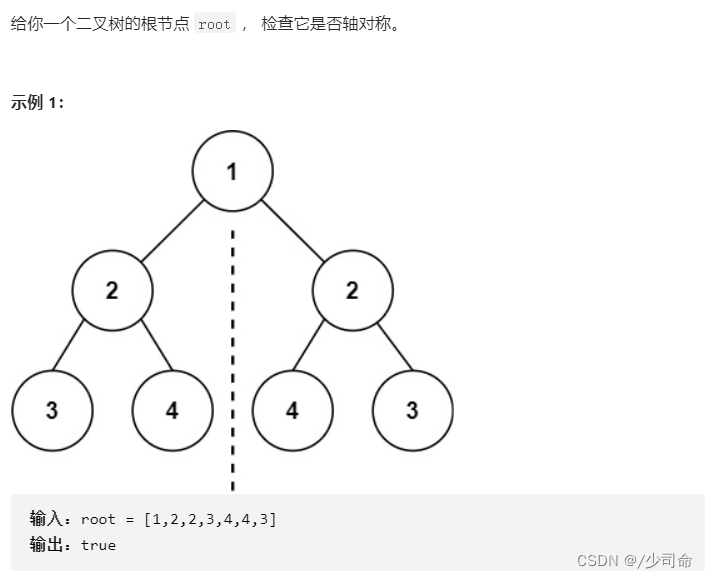
public boolean isSymmetric(TreeNode root) {
if (root == null){
return true;
}
return isSymmetricChild(root.left,root.right);
}
private boolean isSymmetricChild(TreeNode p1, TreeNode p2) {
if (p1 == null || p2 == null){
return p1 == p2;
}
if (p1.val != p2.val){
return false;
}
return isSymmetricChild(p1.left,p2.right) && isSymmetricChild(p1.right,p2.left);
}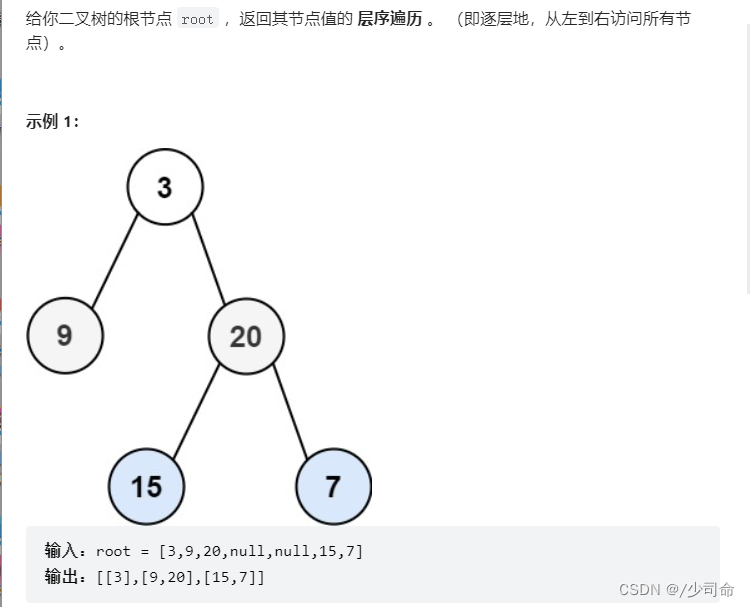
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res= new LinkedList<>();
if (root == null){
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
int size = queue.size();
List<Integer> list = new LinkedList<>();
for (int i = 0; i < size; i++){
TreeNode cur = queue.poll();
list.add(cur.val);
if (cur.left != null){
queue.offer(cur.left);
}
if (cur.right != null){
queue.offer(cur.right);
}
}
res.add(list);
}
return res;
}
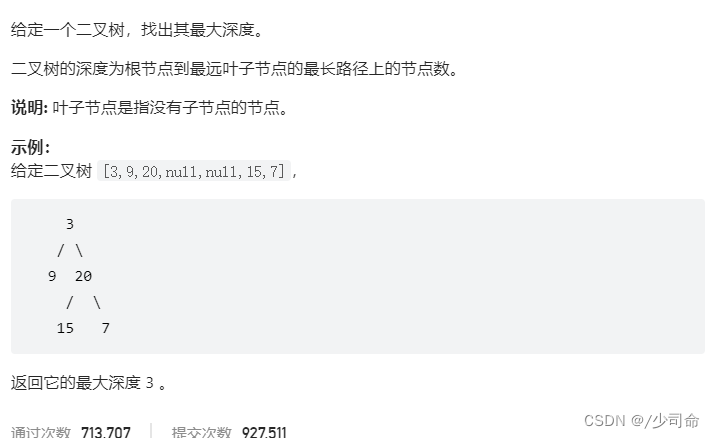
public int maxDepth(TreeNode root) {
if (root == null){
return 0;
}
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return left > right ? left+1 : right+1;
}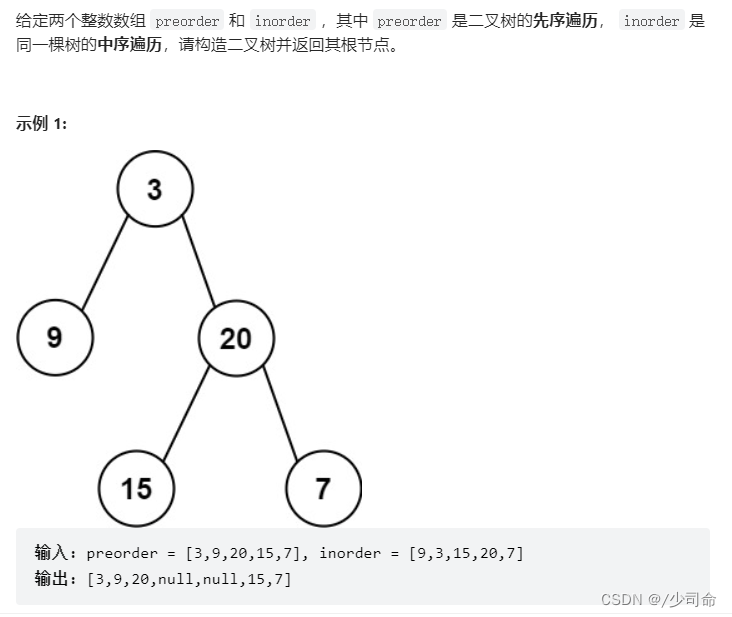
HashMap<Integer,Integer> map = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
for (int i = 0; i < inorder.length; i++){
map.put(inorder[i],i);
}
return build(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
}
private TreeNode build(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) {
if (preStart > preEnd){
return null;
}
int rootVal = preorder[preStart];
int index = map.get(rootVal);
int leftSize = index - inStart;
TreeNode root = new TreeNode(rootVal);
root.left = build(preorder,preStart+1,preStart + leftSize,inorder,inStart,index-1);
root.right = build(preorder,preStart+leftSize+1,preEnd,inorder,index+1,inEnd);
return root;
}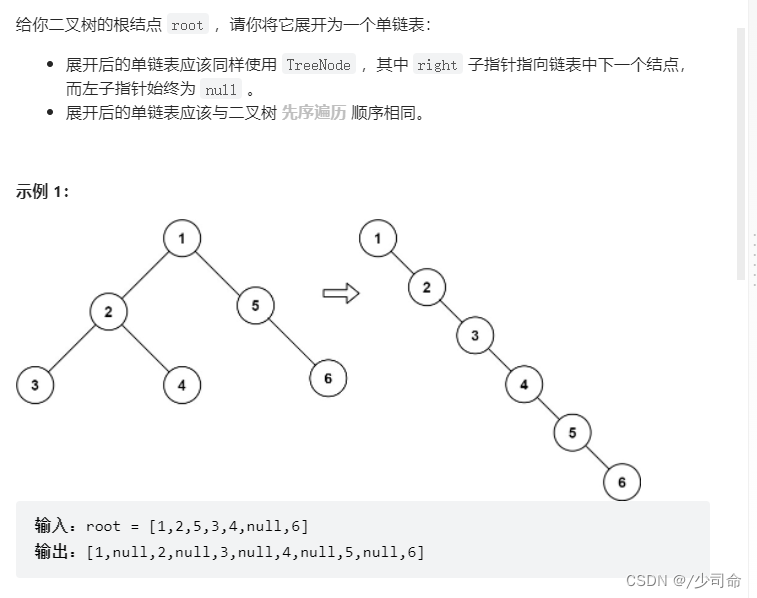
TreeNode pre = null;
public void flatten(TreeNode root) {
if (root == null){
return;
}
flatten(root.right);
flatten(root.left);
root.right = pre;
root.left = null;
pre = root;
}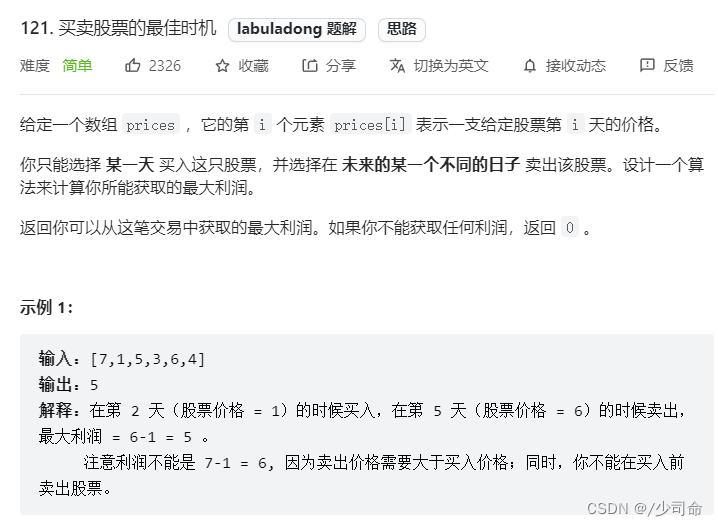
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++){
if ( i-1 == -1){
dp[i][0] = 0;
dp[i][1] = -prices[i];
continue;
}
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1] + prices[i]);
dp[i][1] = Math.max(dp[i-1][1],-prices[i]);
}
return dp[n-1][0];
}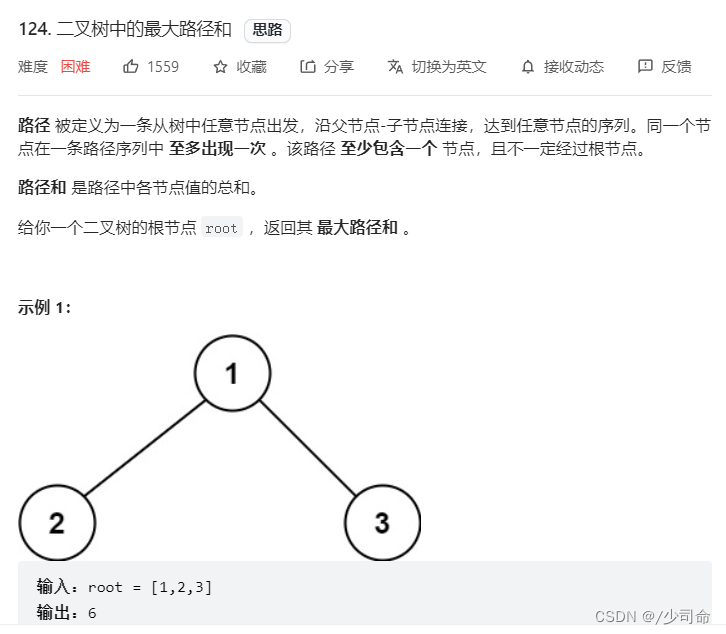
int res = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
if (root == null){
return 0;
}
oneSideMax(root);
return res;
}
private int oneSideMax(TreeNode root) {
if (root == null){
return 0;
}
int leftMaxSum = Math.max(0,oneSideMax(root.left));
int rightMaxSum = Math.max(0,oneSideMax(root.right));
int pathMaxSum = root.val + leftMaxSum + rightMaxSum;
res = Math.max(res,pathMaxSum);
return Math.max(leftMaxSum,rightMaxSum) + root.val;
}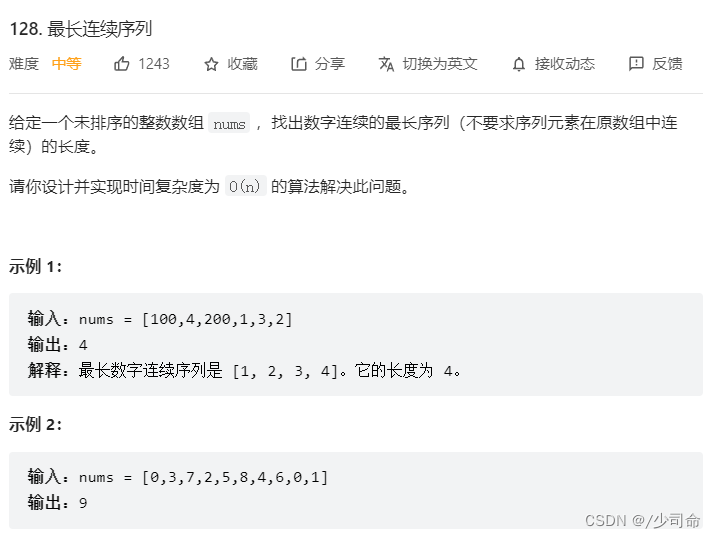
public int longestConsecutive(int[] nums) {
HashSet<Integer> num_set = new HashSet<>();
for (int num: nums){
num_set.add(num);
}
int longestStreak= 0;
for (int num : num_set){
if (! num_set.contains(num-1)){
int currenNum = num;
int currentStreak = 1;
while (num_set.contains(currenNum + 1)){
currenNum++;
currentStreak++;
}
longestStreak = Math.max(longestStreak,currentStreak);
}
}
return longestStreak;
}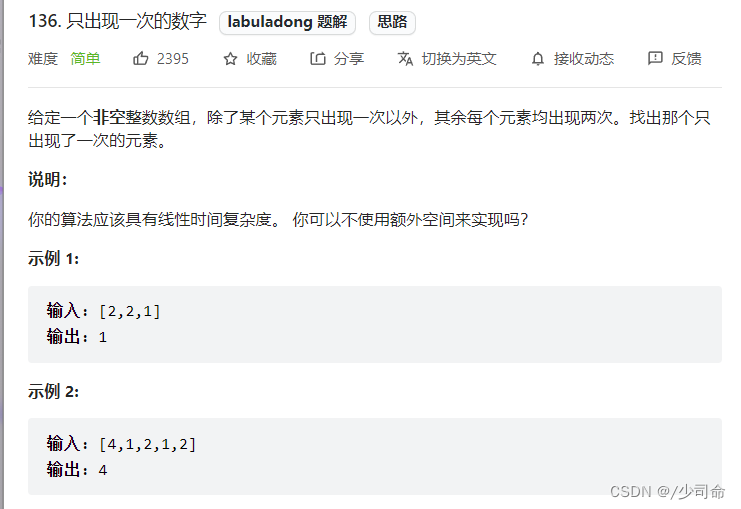
public int singleNumber(int[] nums) {
int res = 0;
for (int n : nums) {
res ^= n;
}
return res;
}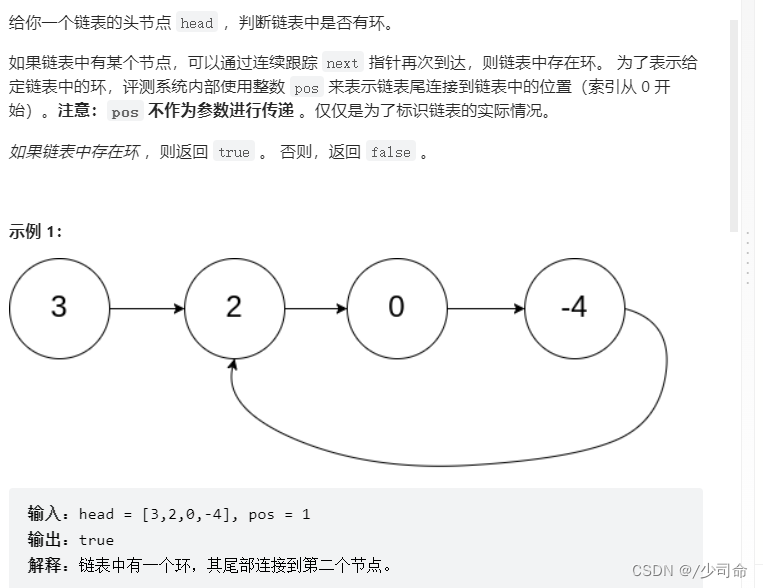
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null){
return false;
}
ListNode slow = head;
ListNode fast = head.next;
while (slow != fast){
if (fast == null || fast.next == null){
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true;
}
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> wordDictSet = new HashSet(wordDict);
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDictSet.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}// 备忘录
int[] memo;
public boolean wordBreak(String s, List<String> wordDict) {
// 备忘录,-1 代表未计算,0 代表 false,1 代表 true
memo = new int[s.length()];
Arrays.fill(memo, -1);
// 根据函数定义,判断 s[0..] 是否能够被拼出
return dp(s, 0, wordDict);
}
// 定义:返回 s[i..] 是否能够被 wordDict 拼出
boolean dp(String s, int i, List<String> wordDict) {
// base case,整个 s 都被拼出来了
if (i == s.length()) {
return true;
}
// 防止冗余计算
if (memo[i] != -1) {
return memo[i] == 1 ? true : false;
}
// 遍历所有单词,尝试匹配 s[i..] 的前缀
for (String word : wordDict) {
int len = word.length();
if (i + len > s.length()) {
continue;
}
String subStr = s.substring(i, i + len);
if (!subStr.equals(word)) {
continue;
}
// s[i..] 的前缀被匹配,去尝试匹配 s[i+len..]
if (dp(s, i + len, wordDict)) {
// s[i..] 可以被拼出,将结果记入备忘录
memo[i] = 1;
return true;
}
}
// s[i..] 不能被拼出,结果记入备忘录
memo[i] = 0;
return false;
}?
