描述
输入两棵二叉树A,B,判断B是不是A的子结构。(我们约定空树不是任意一个树的子结构)
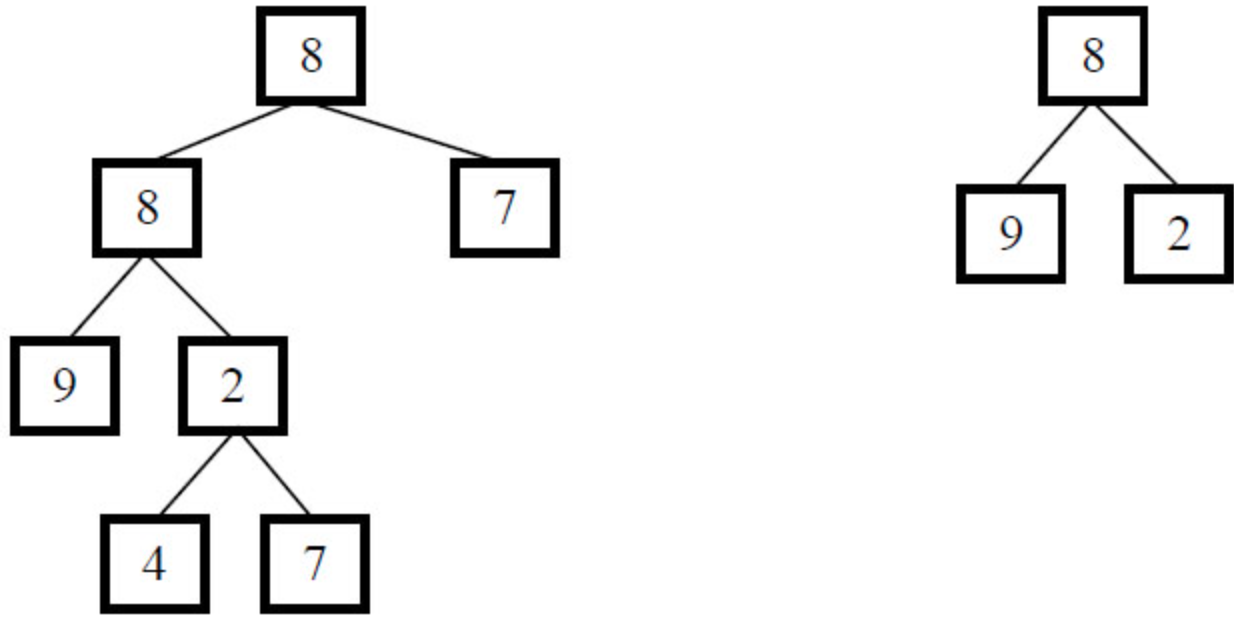
假如给定A为{8,8,7,9,2,#,#,#,#,4,7},B为{8,9,2},2个树的结构如下,可以看出B是A的子结构
数据范围:
0 <= A的节点个数 <= 10000
0 <= B的节点个数 <= 10000
示例1
输入:
{8,8,7,9,2,#,#,#,#,4,7},{8,9,2}
返回值:
true
示例2
输入:
{1,2,3,4,5},{2,4}
返回值:
true
示例3
输入:
{1,2,3},{3,1}
返回值:
false
好难,之前可能没遇到过 第一次做 完全不会
看了解析之后,发现难,难点在于:有两次递归
第一次递归仅仅只是遍历树1的结点而已
找到与 树2根相同的节点时: 再单独将这两个节点作为根,再一起同步遍历判断是否一致
看完解析后,自己敲的代码:
递归代码:
public boolean HasSubtree(TreeNode root1,TreeNode root2) {//只是遍历找匹配的根节点而已
if(root2==null) return false;//空树不是任意一个树的子结构
if(root1==null) return false;//这颗子树肯定没有 返回false
if(root1.val==root2.val) {
//找到与树2根相同得节点了 "摘下"以root1为根的子树开始同步遍历
boolean f0=judge(root1,root2);
if(f0) return true;//找到了直接返回 不递归了
}
boolean f1=HasSubtree(root1.left,root2);//大体结构 先序遍历root1 找与root2根相同的节点
boolean f2=HasSubtree(root1.right,root2);//大体结构 先序遍历root1 找与root2根相同的节点 别忘记改成right
return f1||f2;//左子树或者右子树找到匹配的均可
}
//真正核心 同步遍历了
private boolean judge(TreeNode root1, TreeNode root2) {//此处初始root1 root2一定均不为null
if(root2==null) return true;//root2遍历到null了 root1可以多点没事,正常结尾 这个分支不需要走了
if(root1==null) return false;//此处root2肯定不为null root1却没了 必然不行
if(root1.val!=root2.val){
return false;//严格同步遍历到的值不等 肯定不行
}
//否则就是相等了 继续严格同步遍历下去即可
boolean f1=judge(root1.left,root2.left);//完全严格同步地先序遍历了
boolean f2=judge(root1.right,root2.right);//完全严格同步地先序遍历了
return f1&&f2;//左右子树都重来没有返回false才行
}递归代码2:只是写好后再单纯地在语法层面进行了简化而已 (看起来又好厉害的亚子)
public boolean HasSubtree(TreeNode root1,TreeNode root2) {//只是遍历找匹配的根节点而已
if(root2==null||root1==null) return false;//空树不是任意一个树的子结构
if(root1.val==root2.val && judge(root1,root2)) return true;
return HasSubtree(root1.left,root2)||HasSubtree(root1.right,root2);//左子树或者右子树找到匹配的均可
}
//真正核心 同步遍历了
private boolean judge(TreeNode root1, TreeNode root2) {//此处初始root1 root2一定均不为null
if(root2==null) return true;//root2遍历到null了 root1可以多点没事,正常结尾 这个分支不需要走了 正常结尾返回true
if(root1==null||root1.val!=root2.val) return false;//此处root2肯定不为null root1却没了 必然不行
return judge(root1.left,root2.left)&&judge(root1.right,root2.right);//左右子树都重来没有返回false才行
}方法二:非递归解法 (代码长一点,但是没有递归,确实好理解一点了)
两次层序遍历
第一次,寻找根节点相同的子树
第二次:两树同步层次遍历: 此处其实很简单,以树2为基准判断是否将子节点add进队,树1完全相同操作且一直全部匹配即可
java队列:
add() 和 offer() 方法;二者都是向队列中添加元素
当队列容量超过限制时,add()会报异常,offer()会返回false
public boolean HasSubtree(TreeNode root1,TreeNode root2) {//只是遍历找匹配的根节点而已
if(root2==null||root1==null) return false;
Queue<TreeNode> q=new LinkedList<>();
q.add(root1);
while (!q.isEmpty()){//层序遍历 找与根相同的节点
TreeNode p = q.poll();
if(p.val==root2.val){
if(judge(p,root2)){//看是否完全匹配 千万注意是 p和root2比较 p不要写成了root1
return true;
}
}
if(p.left!=null) q.add(p.left);
if(p.right!=null) q.add(p.right);
}
return false;//前面找到了匹配一定已经返回true了
}
//真正核心 同步遍历了
private boolean judge(TreeNode root1, TreeNode root2) {//此处初始root1 root2一定均不为null
Queue<TreeNode> q1=new LinkedList<>();
Queue<TreeNode> q2=new LinkedList<>();
q1.add(root1);q2.add(root2);
while (!q2.isEmpty()){//以root2为基准 层序遍历root2 root1紧跟一样遍历 能完全匹配上就行
TreeNode p1 = q1.poll();
TreeNode p2 = q2.poll();
if(p1==null) return false;//p2一定不为null p1却没了
if(p1.val!=p2.val) return false;
//接下来就是已经匹配了 得继续匹配其他节点了
if(p2.left!=null){
q1.add(p1.left);
q2.add(p2.left);
}
if(p2.right!=null){
q1.add(p1.right);
q2.add(p2.right);
}
}
return true;//中途没有返回false 说明完全匹配 返回true
}