1 二分查找

有序数组中搜索特定元素
注意:
初始边界条件
mid定义

1.1 二分查找（704）

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

    public int search(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        while(left<=right){
            int mid=left+(right-left)/2;
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]>target){
                right=mid-1;
            }else{
                left=mid+1;
            }
        }
        return -1;

    }

注意：

mid 为什么是int mid=left+(right-left)/2;
解决溢出
如果两个值是 int类型的最大值和int类型的最大值减一两个值相加就溢出了，但是用 left + (right - left) /2求均值不会溢出

1.2 x 的平方根（69）

    public int mySqrt(int x) {
        if(x==0){
            return 0;
        }
        if(x==1){
            return 1;
        }
        int l=1;
        int r=x/2;
        while(l<r){
            int mid=l+(r-l+1)/2;
            if(mid>x/mid){
                r=mid-1;
            }else{
                l=mid;
            }
        }
        return l;

    }

1.3 有效的完全平方数（367）

给定一个正整数 num ，编写一个函数，如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

示例 1：
输入：num = 16
输出：true

示例 2：
输入：num = 14
输出：false

    public boolean isPerfectSquare2(int num) {
        int left = 0, right = num;
        while (left <= right) {
            int mid = (right - left) / 2 + left;
            long square = (long) mid * mid;
            if (square < num) {
                left = mid + 1;
            } else if (square > num) {
                right = mid - 1;
            } else {
                return true;
            }
        }
        return false;
    }

mid 移位

    public boolean isPerfectSquare(int num) {
        long l=0;
        long r=num;
        while(l<r){
            long mid=l+r+1>>1;
            if(mid*mid<=num){
                l=mid;
            }else{
                r=mid-1;
            }
        }
        return r*r==num;
    }

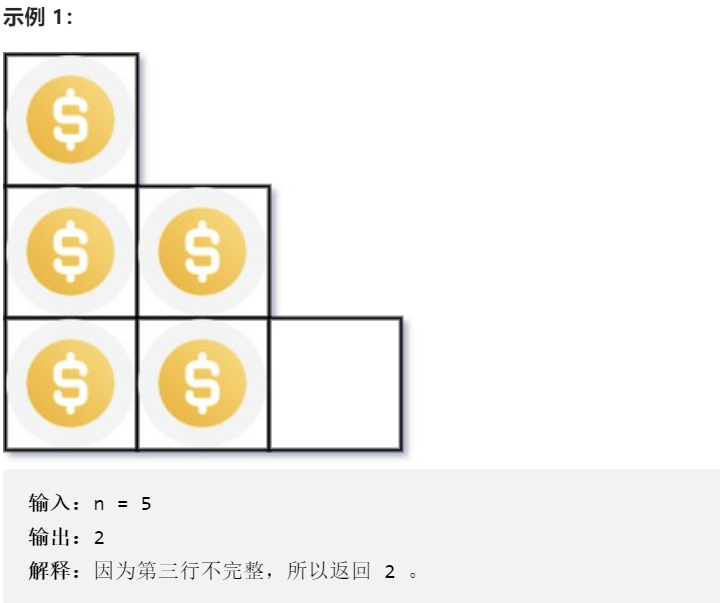
在这里插入图片描述

1.4 排列硬币（441）

你总共有 n 枚硬币，并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯，其第 i 行必须正好有 i 枚硬币。阶梯的最后一行可能是不完整的。
给你一个数字 n ，计算并返回可形成完整阶梯行的总行数。
在这里插入图片描述
等差数列求和公式（首项和公差为1）

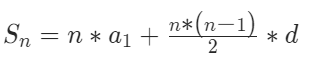
    public int arrangeCoins(int n) {
        int l = 1, r = n;
        while (l < r) {
            int mid = l + (r - l + 1) / 2;
            if (mid * (mid + 1) / 2 <= n) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }

数值溢出
在这里插入图片描述

1.5 长度最小的子数组 (209)

2 递归

2.1 2 的幂

    public boolean isPowerOfTwo(int n) {
      if(n<1){
          return false;
      }
      if (n%2!=0){
          return false;
      }
      if (n==1||n==2){
          return true;
      }
      return isPowerOfTwo(n/2);

    }