原题链接:良好的感觉 - 洛谷
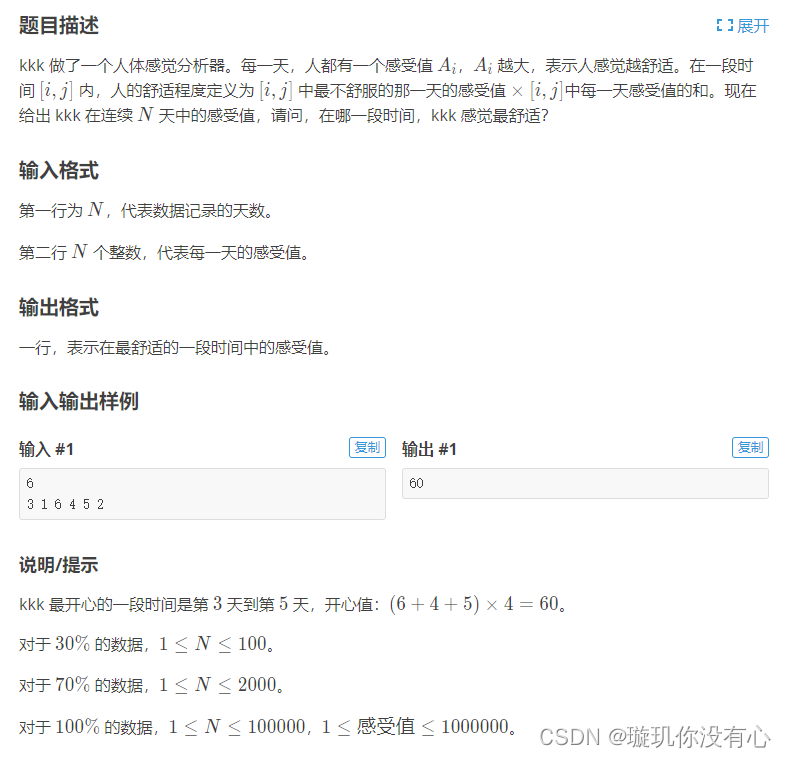 ??
??
思路:枚举区间太复杂了,但是看看,所有区间的最小值最多有n个,那么找到这些最小值枚举最小值以及它们存在的区间就能得到答案。对于a[i]作为最小值的时候,是找它的左边最近的大于它的那个点和右边最近的并且大于它的那个点,然后区间我们就找到了。左边最近比它小、右边最近比它小--->单调栈。从前到后把a[i]的下标i入栈,如果前面有比它大的,就把栈弹出弹出..一直到栈顶的值小于等于a[i],那么这个时候的q[tail]值就是距离a[i]左边最近并小于等于a[i]的下标;同样while循环里就是找到a[q[tail]]右边最近并比其小的值。因为最后一个值进栈会有问题,那么就设一个a[n + 1]为0,就当某些值右边比它小的值了。所以入栈的时候i要从1到n + 1。细节方面还是多注意,答案记得开long long。
AC代码:
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
#define PII pair<int,int>
#define rep(i, n) for (int i = 1; i <= (n); ++i)
#define rrep(i, n) for(int i = n; i >= 1; ++i)
using namespace std;
const double pi = acos(-1.0);
const int N = 1e5 + 10;
int a[N], q[N];
ll f[N], sum[N];
int main()
{
int n;
scanf("%d", &n);
rep(i, n) scanf("%d", &a[i]);
rep(i, n) sum[i] = sum[i - 1] + a[i];
int tail = 0;
a[n + 1] = 0;
for(int i = 1; i <= n + 1; i++) //要到n + 1
{
while(a[i] < a[q[tail]]) //找到a[i]左边最近比它小的值
{
f[q[tail]] += sum[i - 1] - sum[q[tail]]; //q[tail]不是tail
tail--;
}
f[i] = sum[i] - sum[q[tail]];
q[++tail] = i; //记录的是下标
}
ll ans = -1;
rep(i, n) ans = max(ans, 1ll * a[i] * f[i]);
printf("%lld", ans);
return 0;
}
