[数据结构与算法]Leetcode（23）——合并K个升序链表

Leetcode（23）——合并K个升序链表

题目

给你一个链表数组，每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
????1->4->5,
????1->3->4,
????2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

提示：

• k == lists.length
• 0 <= k <= 10^4
• 0 <= lists[i].length <= 500
• -10^4 <= lists[i][j] <= 10^4
• lists[i] 按 升序 排列
• lists[i].length 的总和不超过 10^4

题解

方法一：两两合并直接插入法（自己实现的）

思路

????1. 选取第一段非空序列接在 result 的头结点后面；
????2. 将其它非空序列的元素使用直接插入法从 result 的第一个元素（即最小元素）的位置开始比较并插入；

代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode* result = new ListNode(-1, nullptr);   // 有头结点
        if(lists.empty())  // 即 lists = [] 时直接返回
        {
            delete result;    // 删除头结点
            result = nullptr;
            return result;  
        }
        // 直接插入排序，因为每一段子序列都是有序的，所以默认选取第一段即可
        int i = 0;
        for(auto& t:lists){
            if(t == nullptr) i++;
            else break;
        }
        if(i == lists.size()){
            delete result;      // 删除头结点
            result = nullptr;
            return result;  
        }
        result->next = lists[i];    // 选取第一段非空序列接在 result 的头结点后面

        ListNode *fast = nullptr, *slow = nullptr, *tmp = nullptr;
        for(int n = i+1; n < lists.size(); n++){
            if(lists[n] == nullptr) continue;
            fast = result->next;
            slow = result;
            tmp = lists[n];
            while(tmp != nullptr){  // 直接插入
                if(tmp->val <= fast->val){
                    slow->next = tmp;
                    tmp = tmp->next;
                    slow->next->next = fast;
                    slow = slow->next;  // 只修改 slow 到新添加值上，fast 不变
                }else if(fast->next != nullptr){    // result 全部元素都比该数小
                    slow = fast;
                    fast = fast->next;
                }else{  // tmp 比 result 的全部元素都大，直接将从 tmp 开始的一整个序列加入 result 的 fast 之后
                    fast->next = tmp;
                    break;
                }
            }
        }
        tmp = result;
        result = result->next;
        delete tmp;// 删除头结点
        return result;
    }
};

复杂度分析

时间复杂度：$O(L\times N^2)$ ，$N$ 表示序列的个数，最长序列的长度是 $L$
空间复杂度：$O(1)$

方法二：归并排序

思路

????因为每个序列都是有序的，所以可以选择使用归并排序，并将每个序列看成是最小排序单位，而不是将单一值作为最小排序单位。

代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
 class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if(lists.empty()) return nullptr;
        // 因为每个序列都是有序的，所以可以选择使用归并排序
        int n = lists.size();       // 合并后有几个序列
        vector<ListNode*> TR(lists);// 如果可以的话，直接使用 lists 也行
        while(n != 1){
            for(int i=0; i<n-1; i+=2){
                TR[i/2] = Merge(TR[i], TR[i+1]);
            }
            if(n%2 == 1) TR[n/2+n%2-1] = TR[n-1];
            n = n/2 + n%2;
        }
        return TR[0];
    }
    // 归并排序的核心函数——归并两个序列
    ListNode* Merge(ListNode* A, ListNode* B){
        if(A == nullptr && B == nullptr) return nullptr;    // 两个都是空序列，则直接返回 nullptr
        else if(A == nullptr || B == nullptr){  // 返回非空序列
            if(A == nullptr) return B;
            else return A;
        }

        ListNode *result = nullptr, *tmp = nullptr;         // tmp 用于指向result的最后一个值
        // 先插入一个值，以保证后续操作的代码一致
        if(A->val <= B->val){
            result = A;
            A = A->next;
        }else{
            result = B;
            B = B->next;
        }
        tmp = result;
        while(A != nullptr && B != nullptr){    // 遍历A和B直到任何一个遍历完毕为止
            // 从A和B的开头比较，将较小的插入到result中
            if(A->val <= B->val){
                tmp->next = A;
                A = A->next;
                tmp = tmp->next;
            }else{
                tmp->next = B;
                B = B->next;
                tmp = tmp->next;
            }
        }
        // 将未遍历完的那个序列插到已排序好的result后面
        if(A == nullptr){
            tmp->next = B;
        }else{
            tmp->next = A;
        }
        return result;
    }
};

复杂度分析

时间复杂度：$O(NM\times \log N)$ ，$N$ 表示序列的个数，$M$ 表示所有序列中值的总个数。考虑递归「向上回升」的过程——第一轮合并 $\frac{k}{2}$ 组序列，每一组的时间代价是 $O(2n)$；第二轮合并 $\frac{k}{4}$ 组序列，每一组的时间代价是 $O(4n)$…所以总的时间代价是 $O({\sum }_{i=1}^{\infty }\frac{k}{2^i}\times 2^{i}n)=O(kn\times \log k)$，故渐进时间复杂度为 $O(NM?\log N)$
空间复杂度：上面代码的空间复杂度是 $O(N)$ ，但如果可以使用 lists ，则空间复杂度为 $O(1)$

方法三：优先队列（实际关于它又有两种方法）

思路

方法3.1： 建立优先队列（最大堆或者最小堆均可），全部元素接连入队；最后再不断弹出，构建链表。这也是一种想法，不过这样子效率就有些低下了。
方法3.2： 依然建立优先队列，但不需要全部元素一次性入队；只需要让链表头元素入队即可，弹出该元素后，该链表往后移。

????所以我们在这里选择第二种方法：
????与前面的两个合并序列的方法不同。这次我们需要维护当前每个序列中没有被合并的元素的最前面一个（即每个序列中的当前最小值），$N$ 个链表就最多有 $N$ 个满足这样条件的元素，每次在这些元素里面选取 $\text{val}$ 属性最小的元素合并到答案中。在选取最小元素的时候，我们可以使用优先队列来优化这个过程。

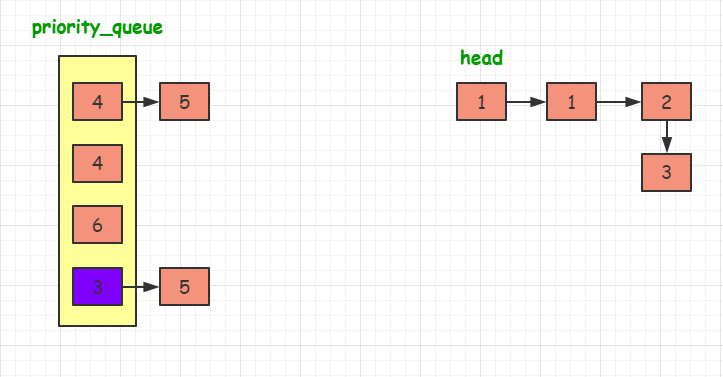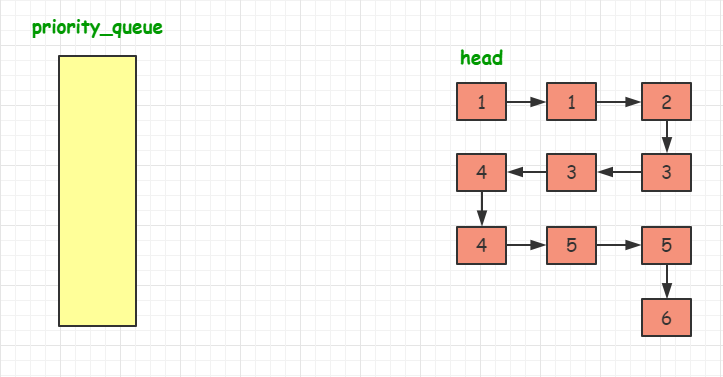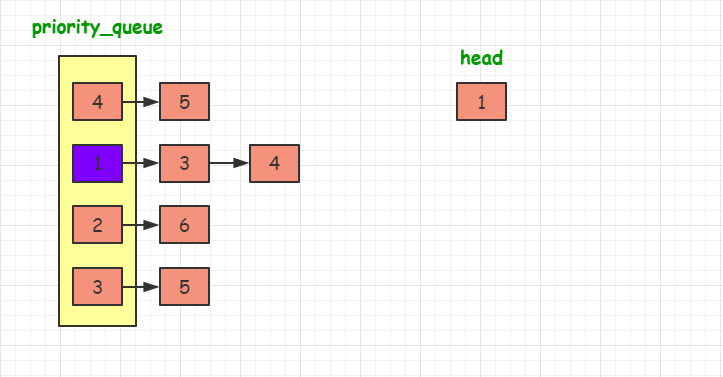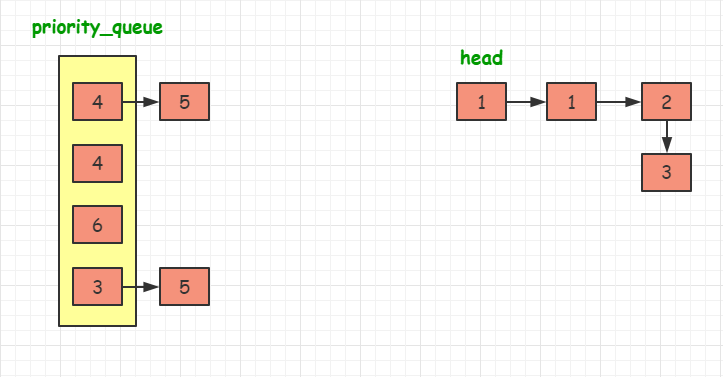
代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
 class Solution {
public:
    // 小根堆的回调函数
    struct cmp{  
        bool operator()(ListNode *a,ListNode *b){
            return a->val > b->val;
        }
    };

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        priority_queue<ListNode*, vector<ListNode*>, cmp> pri_queue;
        // 建立大小为k的小根堆
        for(auto elem : lists){
            if(elem) pri_queue.push(elem);
        }
        // 可以使用哑节点/哨兵节点
        ListNode dummy(-1);
        ListNode* p = &dummy;
        // 开始出队
        while(!pri_queue.empty()){
            ListNode* top = pri_queue.top(); pri_queue.pop();
            p->next = top; p = top;
            if(top->next) pri_queue.push(top->next);
        }
        return dummy.next;  
    }
};

复杂度分析

时间复杂度：$O(NM\times \log N)$ ，$N$ 表示序列的个数，$M$ 表示所有序列中值的总个数
空间复杂度：$O(N)$ ，$N$ 表示序列的个数

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖