解析
比较神奇的一道题。
考虑一个常规套路:把询问离线,移动右端点,维护左端点答案。
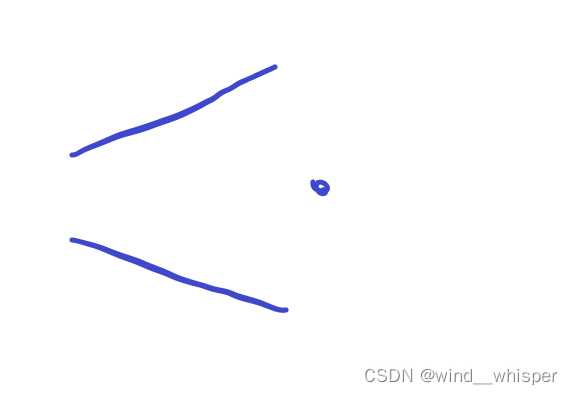
考虑暴力维护,对于当前的
a
i
=
x
a_i=x
ai?=x,左侧如图所示的这两条线上的点都可以产生新的可能答案。
容易构造使得单次产生的新点是
O
(
n
)
O(n)
O(n) 的,无法接受。
如何优化?
一个较为显然的结论是左端点答案单调不降。但这个“单调不降”也可以这么理解:每次询问的是
min
?
i
=
l
r
a
n
s
i
\min_{i=l}^rans_i
mini=lr?ansi?。
那么进而又有一个比较直观的“剪枝“:如果在pos产生的答案不是其右侧的最小值,那么它就一点用的没有。
考虑上线段树,每个节点维护区间答案和区间的所有点,先修改右侧并顺便记录这个右侧的最小值,加上上面的剪枝。
然后它的复杂度就对了。
为什么?
考虑一条线上同时被更新的两个点:
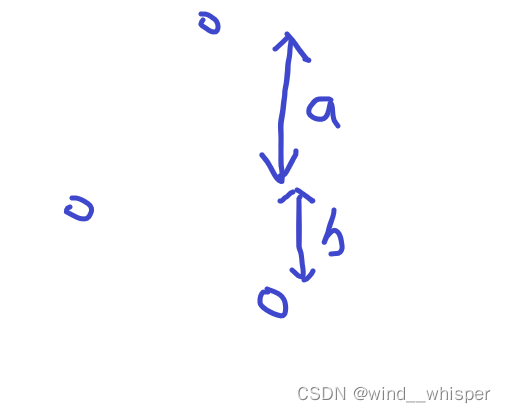
a这个间隔是之前就已经存在的答案,但左侧的点依然被更新了,说明
b
<
a
b<a
b<a。
那么不难发现每次更新一个点,单侧的距离至少减少一半,所以至多只会更新
O
(
log
?
V
)
O(\log V)
O(logV) 个点。
总复杂度
O
(
n
log
?
n
log
?
V
)
O(n\log n\log V)
O(nlognlogV)。
代码
//luogu
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define ok debug("OK\n")
using namespace std;
const int N=4e5+100;
//const int mod=998244353;
inline ll read(){
ll x(0),f(1);char c=getchar();
while(!isdigit(c)) {if(c=='-')f=-1;c=getchar();}
while(isdigit(c)) {x=(x<<1)+(x<<3)+c-'0';c=getchar();}
return x*f;
}
int n,m;
int a[N];
#define mid ((l+r)>>1)
#define ls (k<<1)
#define rs (k<<1|1)
int mn;
struct node{
int ans;
vector<int>v;
}tr[N<<2];
void build(int k,int l,int r){
for(int i=l;i<=r;i++) tr[k].v.push_back(a[i]);
sort(tr[k].v.begin(),tr[k].v.end());
tr[k].ans=2e9;
if(l==r) return;
build(ls,l,mid);
build(rs,mid+1,r);
return;
}
void update(int k,int l,int r,int p,int w){
if(r<=p){
int siz=tr[k].v.size()-1;
//sort(tr[k].v.begin(),tr[k].v.end());
int pos=upper_bound(tr[k].v.begin(),tr[k].v.end(),w)-tr[k].v.begin();
if(pos<=siz) tr[k].ans=min(tr[k].ans,tr[k].v[pos]-w);
pos--;
if(tr[k].v[pos]==w&&r>=p) pos--;
if(pos>=0) tr[k].ans=min(tr[k].ans,w-tr[k].v[pos]);
if(l==r) mn=min(tr[k].ans,mn);
if(tr[k].ans>=mn) return;
}
if(p>mid) update(rs,mid+1,r,p,w);
update(ls,l,mid,p,w);
tr[k].ans=min(tr[ls].ans,tr[rs].ans);
return;
}
int ask(int k,int l,int r,int x,int y){
if(x<=l&&r<=y) return tr[k].ans;
int res=2e9;
if(x<=mid) res=min(res,ask(ls,l,mid,x,y));
if(y>mid) res=min(res,ask(rs,mid+1,r,x,y));
return res;
}
#undef mid
#undef ls
#undef rs
struct query{
int l,id;
};
int ans[N];
vector<query>q[N];
signed main(){
#ifndef ONLINE_JUDGE
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
#endif
n=read();
for(int i=1;i<=n;i++) a[i]=read();
m=read();
for(int i=1;i<=m;i++){
int l=read(),r=read();
q[r].push_back((query){l,i});
}
build(1,1,n);
for(int i=1;i<=n;i++){
mn=2e9;
update(1,1,n,i,a[i]);
for(query o:q[i]){
ans[o.id]=ask(1,1,n,o.l,i);
}
}
for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
/*
*/
