
fprintf('解析解.\n');
syms t x y
[x,y] = dsolve('D2x=-2*x-3*Dx+exp(-5*t)',' D2y==2*x-3*y-4*Dx-4*Dy-sin(t)','x(0)=1','Dx(0)=2','y(0)=3','Dy(0)=4')
x = simplify(x); y = simplify(y);
fprintf('数值解.\n');
[t1,x1] = ode45('myfun',[0,10],[1;2;3;4]);
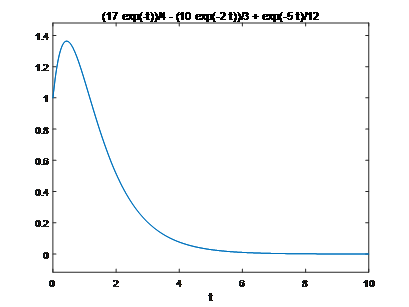
ezplot(x,[0,10]), line(t1,x1(:,1));
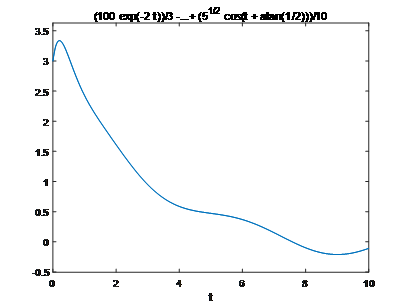
figure; ezplot(y,[0,10]), line(t1,x1(:,3))
function dx=myfun(t,x)
dx=[x(2);
-2*x(1)-3*x(2)+exp(-5*t);
x(4);
2*x(1)-3*x(3)-4*x(2)-4*x(4)-sin(t)];
输出
%解析解.
x =
exp(-2*t)*(exp(-3*t)/3 - 10/3) - 2*exp(-t)*(exp(-4*t)/8 - 17/8)
y =
(8*exp(-t) - 6*t*exp(-t))*(exp(-4*t)/8 - 17/8) - 10*exp(-2*t)*(exp(-3*t)/3 - 10/3) - 2*exp(-3*t)*((exp(3*t)*(cos(t) - 3*sin(t)))/40 - (7*exp(-2*t))/8 + 71/10) + 6*exp(-t)*((exp(t)*((13*exp(-5*t))/8 + cos(t)/2 - sin(t)/2 + (3*t*exp(-5*t))/2))/12 + 7/96)
数值解.

fprintf('解析解.\n');
syms t y1 y2;
[y1,y2] = dsolve('Dy1=9*y1+24*y2+5*cos(t)-1/3*sin(t)','Dy2=-24*y1-51*y2-9*cos(t)+1/3*sin(t)','y1(0)=1/3','y2(0)=2/3')
y1 = simplify(y1)
y2 = simplify(y2)
fprintf('数值解.\n');
[t,y]=ode45('myfun1',[0,100],[0;1]); %[t,y]=ode15s('myfun1',[0,100],[0;1]);
plot(t,y) % 状态变量曲线
输出
解析解.
y1 =
(2*exp(-3*t))/3 - (2*exp(-39*t))/3 + cos(t)/3
y2 =
(4*exp(-39*t))/3 - exp(-3*t)/3 - cos(t)/3
数值解.
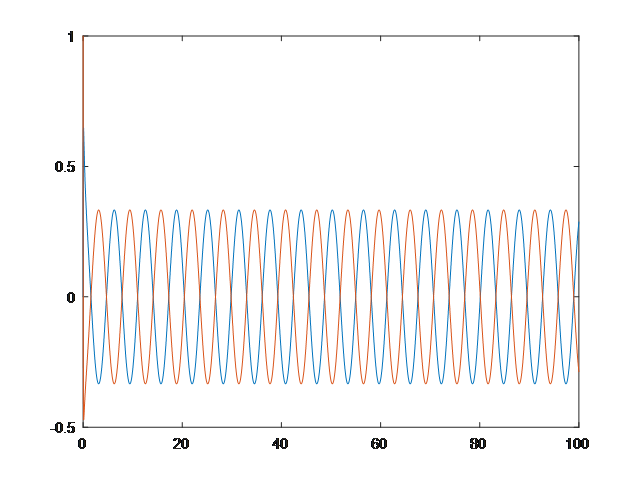
figure,%误差
y1 = (2*exp(-3*t))/3 - (2*exp(-39*t))/3 + cos(t)/3;
y2 = (4*exp(-39*t))/3 - exp(-3*t)/3 - cos(t)/3;
err1 = y1 - y(:,1);
err2 = y2 - y(:,2);
plot(t,err1,t,err2);
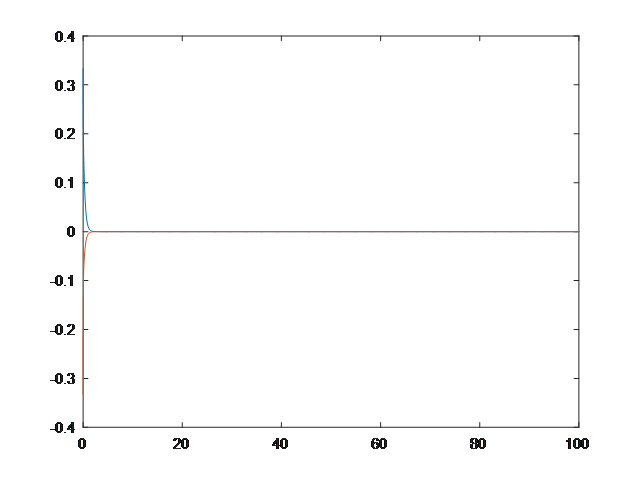

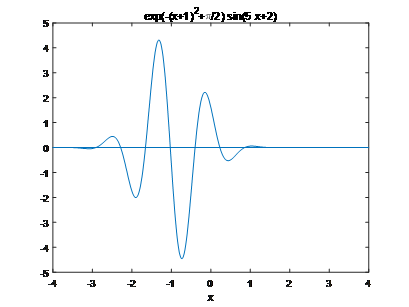
fprintf('一元函数.\n');
ezplot('exp(-(x+1)^2+pi/2)*sin(5*x+2)',[-4 4]),axis([-4 4 -5 5]);
hold on,
line([-4,4],[0,0])
x0 = 1.4857; vpa(exp(-(x0+1)^2+pi/2)*sin(5*x0+2))
%vpa(subs(exp(-(x+1)^2+pi/2)*sin(5*x+2)',x,x0))
syms x ; S = solve(exp(-(x+1)^2+pi/2)*sin(5*x+2)==0,x);
x=S; vpa(eval('exp(-(x+1)^2+pi/2)*sin(5*x+2)'))
syms x ; [x,fval,exitflag] = fzero('exp(-(x+1)^2+pi/2)*sin(5*x+2)',-0.5)
vpa(eval('exp(-(x+1)^2+pi/2)*sin(5*x+2)'))
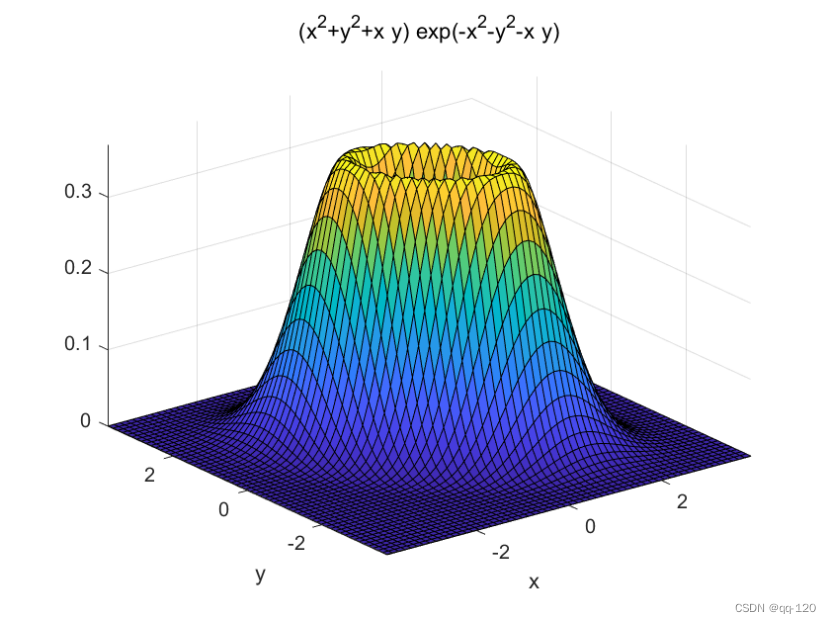
fprintf('二元函数.\n');
figure,ezsurf('(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)')
[x,y] = meshgrid(-3:.1:3); % 生成网格型矩阵
z = (x.^2+y.^2+x.*y).*exp(-x.^2-y.^2-x.*y); % 计算出矩阵上各点的高度
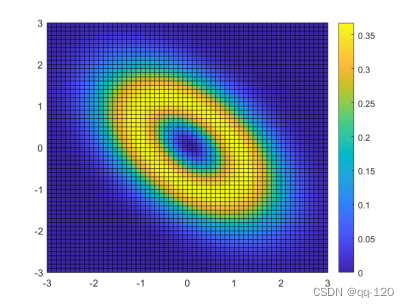
figure; surface(x,y,z); colorbar;
figure; [C,h]=contour(x,y,z,[-0.1:0.05:0.1]);
% x = 0; y = 0; vpa((x^2+y^2+x*y)*exp(-x^2-y^2-x*y))
syms x y;
y1 = solve((x^2+y^2+x*y)*exp(-x^2-y^2-x*y)==0,y)
y2 = simplify(subs((x^2+y^2+x*y)*exp(-x^2-y^2-x*y),y,y1))
x = y2(1),y = y2(2);
vpa((x^2+y^2+x*y)*exp(-x^2-y^2-x*y))
% % OPT = optimset; OPT.LargeScale='off';
% % x = fsolve('my2deqq',[0.2;0.2],OPT) %如果增加一个条件x=y,可以用这几行代码
% % y = x(2,1), x = x(1,1); vpa(eval('(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)'))
输出
一元函数.
ans =
-0.00003711853740029228201913191753647
ans =
0.0
x =
-0.4000
fval =
0
ans =
0.0
二元函数.
ans =
0.0
y1 =
- x/2 - (3^(1/2)*x*1i)/2
- x/2 + (3^(1/2)*x*1i)/2
y2 =
0
0
x =
0
ans =
0.0
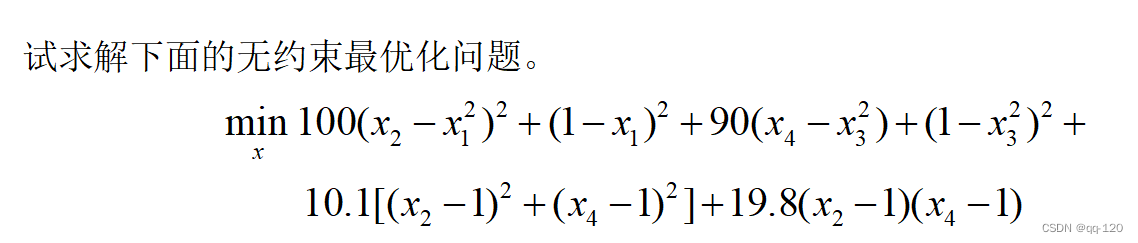
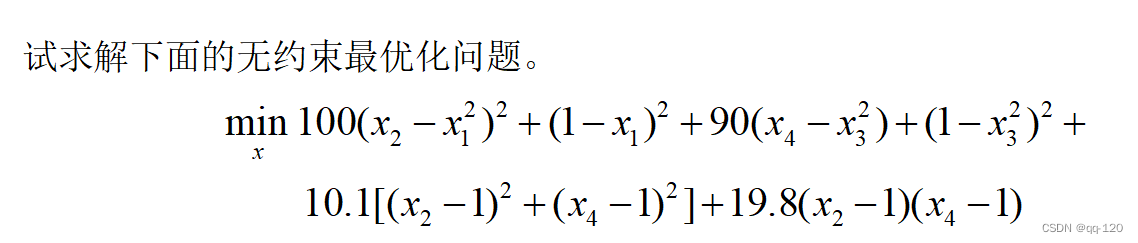
fun = inline(['100*(x(2)-x(1)^2)^2+(1-x(1))^2+90*(x(4)-x(3)^2)' ...
' +(1-x(3)^2)^2+10.1*((x(2)-1)^2+(x(4)-1)^2)+19.8*(x(2)-1)*(x(4)-1)'],'x')
x0 = [0;0;0;0];
options = optimset('PlotFcns',@optimplotfval);
options.Display='iter';
% [x,fval,exitflag,output] = fminsearch(fun,x0,options)
[x,fval,exitflag,output] = fminunc(fun,x0,options)
输出
x =
10.5464
111.2321
6.7823
-111.5047
fval =
-7.0465e+03
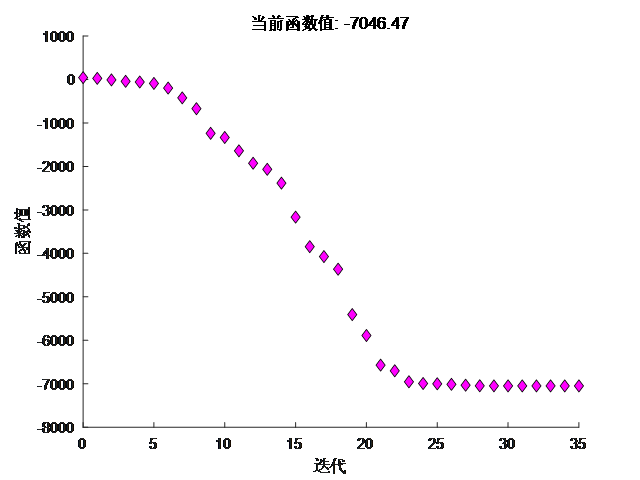

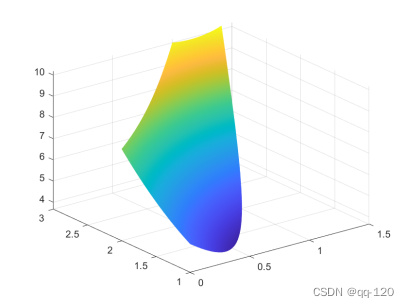
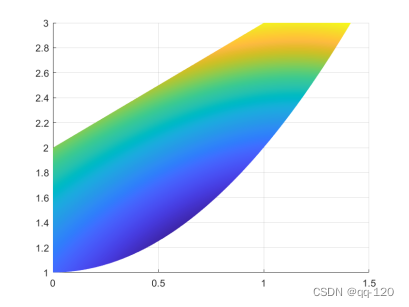
[x1,x2] = meshgrid(0:.001:3); % 生成网格型矩阵
z = x1.*x1.*x1+x2.*x2-4.*x1+4; % 计算出矩阵上各点的高度
i = find(-x1.^2+x2<1); z(i)=NaN; % 找出-x1^2+x2>1的坐标,并置函数值为NaN
i = find(x1-x2+2<0); z(i)=NaN; % 找出x1-x2+2>0的坐标,置为 NaN
i = find(x1<0); z(i)=NaN; i = find(x2<0); z(i)=NaN;
figure,surf(x1,x2,z); shading interp;
min(z(:)), view(0,90)
输出
ans =
3.6608
ff = optimset; ff.LargeScale = 'off'; ff.Display = 'iter';
ff.TolFun = 1e-30; ff.TolX = 1e-15; ff.TolCon = 1e-20;
x0 = [1;1]; xm = [0;0]; xM = []; A = []; B = []; Aeq = []; Beq = [];
[x,fval,exitflag,output] = fmincon('hm_fun1',x0,A,B,Aeq,Beq,xm,xM, 'hm_con1',ff) ;
x, fval, kk = output.funcCount
function y = opt_fun1(x)
y = x(1)*x(1)*x(1)+x(2)*x(2)-4*x(1)+4;
function [c,ceq]= opt_con1(x)
c = [-x(1)+x(2)-2; x(1)*x(1)-x(2)+1];
ceq = [];
输出
x =
0.570399895591170
1.325356040965869
fval =
3.660552104713893
kk =
81

f = [0,0,0,0,0,1,1]';
A=[]; B=[]; Ae=[1,1,1,1,0,0,0;-2,1,-1,0,0,-1,1;0,3,1,0,1,0,1]; Be=[4;1;9]; xm=[0,0,0,0,0,0,0];
ff = optimset;
ff.TolX=1e-15; ff.Display='iter';
[x,fval,exitflag,output]=linprog(f,A,B,Ae,Be,xm,[],[],ff)
输出
x =
0
1
0
3
6
0
0
fval =
0
exitflag =
1

H = [4,-4; -4,8]; f = [-6;-3];
OPT=optimset; OPT.LargeScale='off'; % 不使用大规模问题算法
A=[1,1; 4,1]; B=[3; 9]; Aeq=[]; Beq=[]; LB=zeros(2,1);
[x,f_opt] = quadprog(H,f,A,B,Aeq,Beq,LB,[],[],OPT)
x =
1.949999999999998
1.050000000000002
f_opt =
-11.025000000000000

ff = optimset; ff.LargeScale = 'off'; ff.Display = 'iter';
x0 = [5;5]; xm = [-10;-10]; xM = [10;10]; A = []; B = []; Aeq = []; Beq = [];
[x,fval,exitflag,output] = fmincon('opt_funn2',x0,A,B,Aeq,Beq,xm,xM, 'opt_conn2',ff) ;
x, fval, kk = output.funcCount
% x0 = [0,0]时,x = [1.182497275912064,-1.739766923623964];
function y=opt_funn2(x)
y=exp(x(1))*(4*x(1)*x(1)+2*x(2)*x(2)+4*x(1)*x(2)+2*x(2)+1);
function [c,ceq]= opt_conn2(x)
c = [x(1)+x(2); x(1)*x(2)-x(1)-x(2)+1.5; -x(1)*x(2)-10];
ceq = [];
输出
x =
-9.5474
1.0474
fval =
0.0236
kk =
59

fprintf('0-1线性规划解法.\n');
f = [5,7,10,3,1]; A=[-1 1 -5 -1 4; 2 -6 3 2 -2; 0 -2 2 -1 -1]; B=[-2;0;1];
[x,fval,exitflag,output] = intlinprog(f,[1,2,3],A,B,[],[],zeros(5,1),ones(5,1))
fprintf('穷举方法.\n');
[x1,x2,x3,x4,x5] = ndgrid([0,1],[0,1],[0,1],[0,1],[0,1]);
i=find((x1-x2+5*x3+x4-4*x5>=2) & (-2*x1+6*x2-3*x3-2*x4+2*x5>=0) & (-2*x2+2*x3-x4-x5<=1));
f=5*x1(i)+7*x2(i)+10*x3(i)+3*x4(i)+x5(i); [fmin,ii]=sort(f);
index=i(ii(1)); x = [x1(index),x2(index),x3(index),x4(index),x5(index)]
输出
x =
0
1
1
0
0
fval =
17
exitflag =
1
穷举方法.
x =
0 1 1 0 0
