一、图的基本常识

1、弧头和弧尾

有向图中，无箭头一端的顶点通常被称为"初始点"或"弧尾"，箭头直线的顶点被称为"终端点"或"弧头"。

2、入度和出度

对于有向图中的一个顶点 V 来说，箭头指向 V 的弧的数量为 V 的入度（InDegree，记为 ID(V)）；箭头远离 V 的弧的数量为 V 的出度（OutDegree，记为OD(V)）。

3、(V1,V2) 和 <V1,V2> 的区别

无向图中描述两顶点（V1 和 V2）之间的关系可以用 (V1,V2) 来表示
有向图中描述从 V1 到 V2 的"单向"关系用 <V1,V2> 来表示。

由于图存储结构中顶点之间的关系是用线来表示的，因此 (V1,V2) 还可以用来表示无向图中连接 V1 和 V2 的线，又称为边；
<V1,V2> 也可用来表示有向图中从 V1 到 V2 带方向的线，又称为弧。

4、集合 VR 的含义

图中习惯用 VR 表示图中所有顶点之间关系的集合。
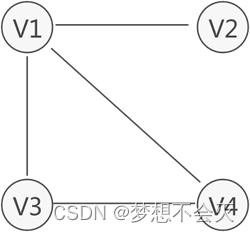
在这里插入图片描述
例如，上图中无向图的集合 VR={(v1,v2),(v1,v4),(v1,v3),(v3,v4)}，

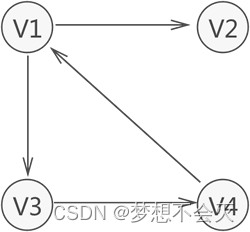
上图中有向图的集合 VR={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}。

5、路径和回路

无论是无向图还是有向图，从一个顶点到另一顶点途径的所有顶点组成的序列（包含这两个顶点），称为一条路径。如果路径中第一个顶点和最后一个顶点相同，则此路径称为"回路"（或"环"）。

并且，若路径中各顶点都不重复，此路径又被称为"简单路径"；同样，若回路中的顶点互不重复，此回路被称为"简单回路"（或简单环）。

二、图的遍历

1、广度优先搜索（Breadth First Search，BFS）

广度优先搜索的搜索策略是尽可能深地搜索一个图。
基本思想是：首先访问图中某一未访问的顶点V1，然后由V1出发，访问与V1邻接且未被访问的任一顶点V2，再访问与V2邻接且未被访问的任一顶点V3，……重复上述过程。当不能再继续向下访问(即孤立点)时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直到图中所有顶点均被访问过为止。

2、深度优先搜索（Depth First Search，DFS）

深度优先搜索的基本思想是：首先访问起始顶点v，接着由v出发，依次访问v的各个未访问过的邻接顶点w1，w2，…，wi，然后再依次访问w1，w2，…，wi的所有未被访问过的邻接顶点；再从这些访问过的顶点出发，再访问它们所有未被访问过的邻接顶点……依次类推，直到图中所有顶点都被访问过为止。

三、拓扑排序(Topological Sorting)

1、定义

维基百科上拓扑排序的定义为

对于任何有向无环图(Directed Acyclic
Graph，DAG)而言，其拓扑排序为其所有结点的一个线性排序(同一个有向图可能存在多个这样的结点排序)。该排序满足这样的条件——对于图中的任意两个结点U和V，若存在一条有向边从U指向V，则在拓扑排序中U一定出现在V前面。

2、必备条件

每个顶点出现且只出现一次。
若存在一条从顶点A到顶点B的路径，那么在序列中顶点 A出现在顶点 B的前面。

四、如何找出一个有向图的拓扑排序？

假设有向图中不存在起点和终点为同一结点的有向边，即该图为有向无环图
步骤如下：

从DAG图中选择一个入度为0的顶点并输出。
从图中删除该顶点和所有以它为起点的有向边。
重复1和2直到当前的DAG图为空或当前图中不存在入度为0的顶点为止。后一种情况说明有向图中必然存在环。

例如下方的DAG图
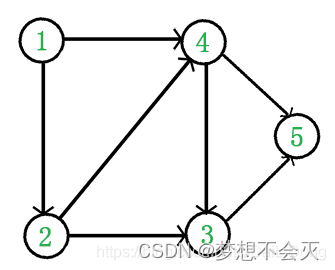
在这里插入图片描述
结点1的入度：0，出度：2
结点2的入度：1，出度：2
结点3的入度：2，出度：1
结点4的入度：2，出度：2
结点5的入度：2，出度：0
它的拓扑排序流程如下图所示：

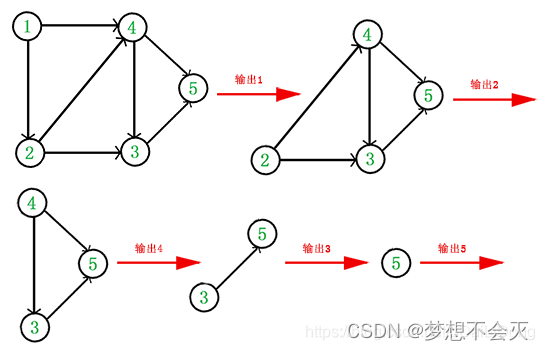
于是，得到拓扑排序后的结果是: {1,2,4,3,5} 。
如果没有结点2 —> 结点4的这个箭头，那么如下：
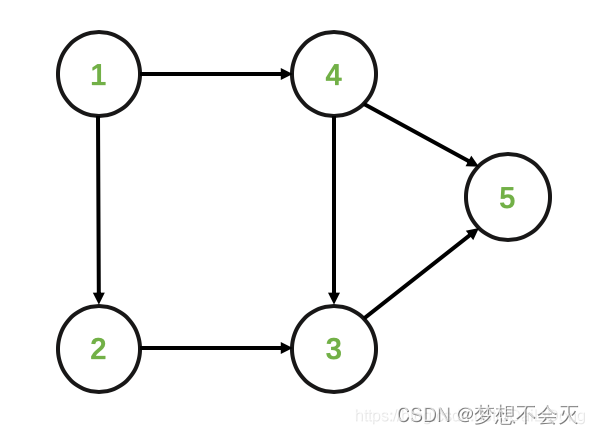
在这里插入图片描述
我们可以得到它的拓扑排序为：{1,2,4,3,5} 或者 {1,4,2,3,5} ，即对同一DAG图来说，它的拓扑排序结果可能存在多个。

我们可以使用一个改进的深度优先遍历或广度优先遍历算法来完成拓扑排序。以广度优先遍历为例，这一改进后的算法与普通的广度优先遍历唯一的区别在于我们应当保存每一个结点对应的入度，并在遍历的每一层选取入度为0的结点开始遍历（而普通的广度优先遍历则无此限制，可以从任意一个结点开始遍历）。
这个算法描述如下：

初始化一个数据结构来保存每一个结点的入度。
对于图中的每一个结点的子结点，将其子结点的入度加1。
选取入度为0的任意一个结点开始遍历，并将该节点加入输出。
对于遍历过的每个结点，更新其子结点的入度：将子结点的入度减1。
重复步骤3，直到遍历完所有的结点。
如果无法遍历完所有的结点，则意味着当前的图不是有向无环图。不存在拓扑排序。

五、用Java实现有向无环图的拓扑排序

例题如下：
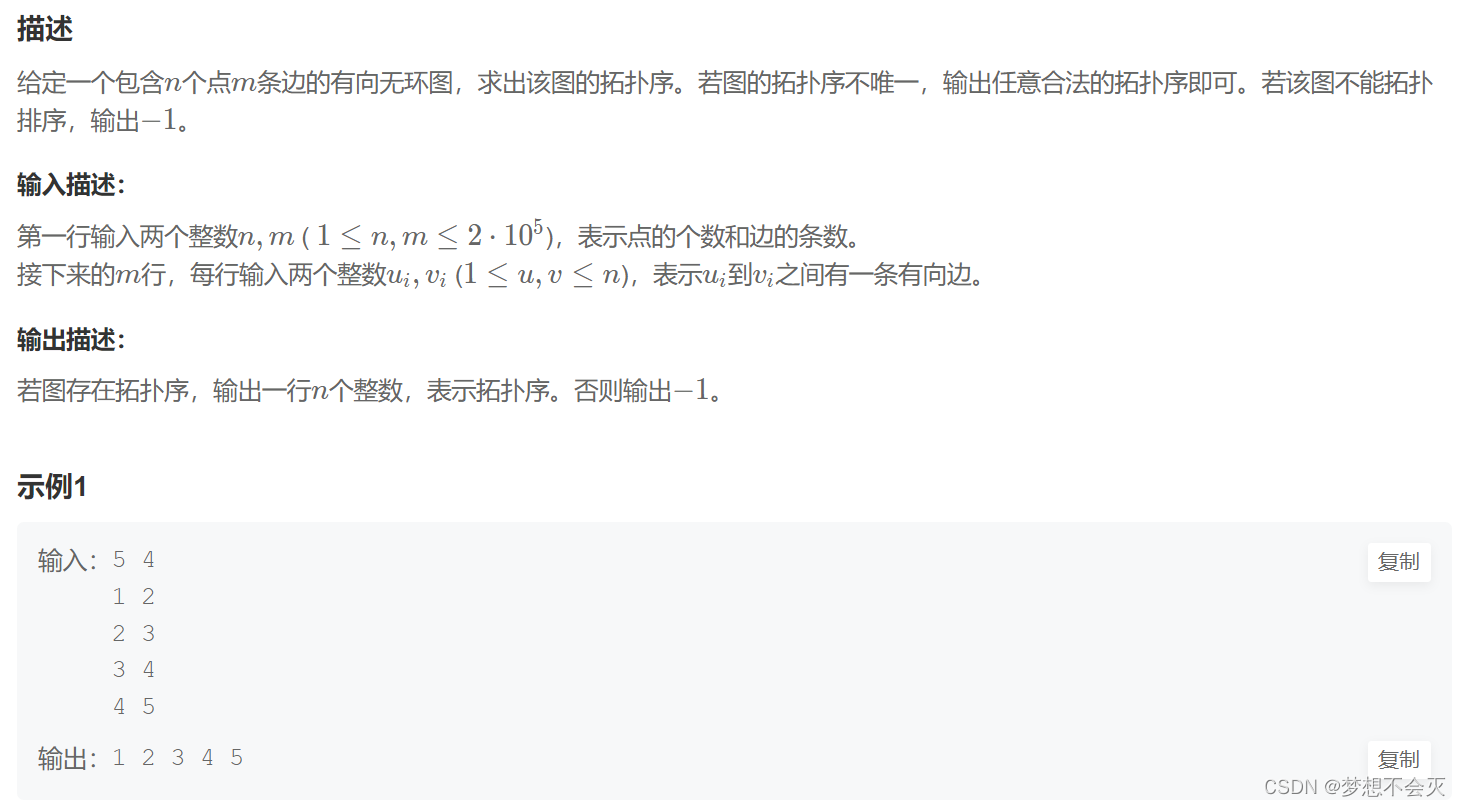
在这里插入图片描述
代码如下：

import java.io.*;
import java.util.*;

/**
 * 拓扑排序
 */
public class Solution4 {
    /**
     * 拓扑序
     */
    static List<Integer> ans = new ArrayList<>();

    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
        String[] line = reader.readLine().split(" ");
        // 存储点的出度集合
        List<List<Integer>> graph = new ArrayList<>();
        // 点数
        int n = Integer.parseInt(line[0]);
        // 边数
        int m = Integer.parseInt(line[1]);
        // 存储点的入度数
        int[] inDegree = new int[n];
        // 初始化点
        for (int i = 0; i < n; i++) {
            // 此处由于点的出度可能有多个,则使用list初始化
            graph.add(new ArrayList<>());
        }
        for (int i = 0; i < m; i++) {
            line = reader.readLine().split(" ");
            // 边的初始点
            int u = Integer.parseInt(line[0]);
            // 边的终端点
            int v = Integer.parseInt(line[1]);
            // v点入度+1
            inDegree[v - 1]++;
            // u点增加出度,指向v点
            graph.get(u - 1).add(v - 1);
        }
        boolean flag = topologicalSort(graph, inDegree);
        if (flag) {
            // 是有向无环图,输出拓扑排序
            for (int i = 0; i < ans.size(); i++) {
                writer.write(String.valueOf(ans.get(i)));
                if (i != n - 1) {
                    writer.write(" ");
                }
            }
        } else {
            writer.write("-1");

        }
        writer.flush();
        writer.close();

    }

    public static boolean topologicalSort(List<List<Integer>> graph, int[] inDegree) {
        int num = 0;
        Deque<Integer> deque = new ArrayDeque<>();
        for (int i = 0; i < inDegree.length; i++) {
            // 先找入度为0的点,放入队列
            if (inDegree[i] == 0) {
                deque.offer(i);

            }
        }
        while (!deque.isEmpty()) {
            int u = deque.poll();
            // 入度为0的点为起始点
            ans.add(u + 1);
            for (int i = 0; i < graph.get(u).size(); i++) {
                // 获取入度为0的点的出度点
                int v = graph.get(u).get(i);
                // 这个点的入度减1
                inDegree[v]--;
                // 寻找下一个入度为0的点
                if (inDegree[v] == 0) {
                    deque.offer(v);
                }
            }
            graph.get(u).clear();
            num++;
        }
        // 若此时输出的结点数不等于有向图中的顶点数，则说明有向图中存在回路，否则输出的顶点的顺序即为一个拓扑序列
        return num == inDegree.length;
    }
}