题目:
Given two integer arrays?inorder?and?postorder?where?inorder?is the inorder traversal of a binary tree and?postorder?is the postorder traversal of the same tree, construct and return?the binary tree.
Example 1:
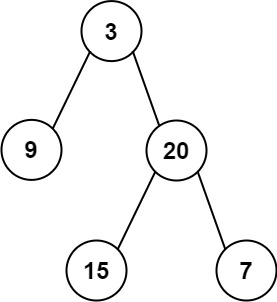
Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] Output: [3,9,20,null,null,15,7]
Example 2:
Input: inorder = [-1], postorder = [-1] Output: [-1]
Constraints:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder?and?postorder?consist of?unique?values.- Each value of?
postorder?also appears in?inorder. inorder?is?guaranteed?to be the inorder traversal of the tree.postorder?is?guaranteed?to be the postorder traversal of the tree.
思路:
已知前序和后序数组建立树,比较经典的二叉树题目了。我们要掌握的基础知识:后序的最后一个数字即是根(题目保证每个数字不同),而根据后序的数字,假设为x,在中序数组中,x之前的子数组就是x的左子树的,假设长为len1;x之后的子数组就是右子树的,假设长为len2。在后序数组中,前len1个数字组成的子数组就是左子树的,而len1之后的len2个数字组成的子数组就是右子树的。掌握以上几点很重要,这使我们确认切割的点位。递归中,首先如果进来的两个数组是空的,那么就返回nullptr。然后开始正式建立树:1)以后序数组的最后一个数字建立root;2)切割中序数组,将其分为左右两段,分别是root数字的左侧子数组和右侧子数组;3)用中序数组的两个子数组长度切割后序子数组,这一过程中记得消去最后一个已经作为root的数字;4)向root的左右子树递归;5)返回root。总的来说在已知上面的基础知识情况下,只要小心数组的切割点位即可。
代码:
/**
?* Definition for a binary tree node.
?* struct TreeNode {
?* ? ? int val;
?* ? ? TreeNode *left;
?* ? ? TreeNode *right;
?* ? ? TreeNode() : val(0), left(nullptr), right(nullptr) {}
?* ? ? TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
?* ? ? TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
?* };
?*/
class Solution {
public:
? ? TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
? ? ? ? TreeNode* root = traversal(inorder, postorder);
? ? ? ? return root;
? ? }
private:
? ? TreeNode* traversal(vector<int> &inorder, vector<int> &postorder) {
? ? ? ? if (inorder.empty() || postorder.empty())
? ? ? ? ? ? return nullptr;
? ? ? ? TreeNode* root = new TreeNode(postorder.back());
? ? ? ? int cur = 0;
? ? ? ? for (; cur < inorder.size(); cur++) {
? ? ? ? ? ? if (inorder[cur] == root->val)
? ? ? ? ? ? ? ? break;
? ? ? ? }
? ? ? ? vector<int> inorderleft(begin(inorder), begin(inorder) + cur);
? ? ? ? vector<int> inorderright(begin(inorder) + cur + 1, end(inorder));
? ? ? ? postorder.pop_back();
? ? ? ? vector<int> postorderleft(begin(postorder), begin(postorder) + inorderleft.size());
? ? ? ? vector<int> postorderright(begin(postorder) + inorderleft.size(), end(postorder));
? ? ? ? root->left = traversal(inorderleft, postorderleft);
? ? ? ? root->right = traversal(inorderright, postorderright);
? ? ? ? return root;
? ? }
};
