题目

Example:
4
1
2
3
4
output:
0
1
2
2
思路
如下图,我们打表可以发现在长度
1
e
9
1e9
1e9,最大不过一个二进制数字长度为
29
29
29。
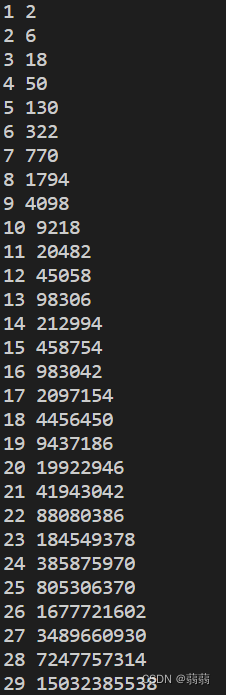
那我们用高中数学的数列求和公式可以求出
L
(
n
)
=
2
n
×
(
n
?
1
)
+
2
L(n) = 2^{n}\times(n-1)+2
L(n)=2n×(n?1)+2
表示以二进制数字长度为
n
n
n的最后一个数字结尾可以得到的
p
k
p_k
pk?的长度。
然后这题是个找规律的题,
如下面一段字符串,我们可以知道是以
8
8
8的二进制结尾。
0110111001011101111000
假设我们输入的
k
k
k为
18
18
18,结合打表得到的数据可以知道,我们得到的答案为
3
3
3,但是如果
k
k
k为
19
19
19,答案就为
4
4
4,因此我们可以发现,连续为
1
1
1的子字符串的最大长度的变化在二进制数字长度变化的交界处。
下面看代码更便于理解
代码
#include<bits/stdc++.h>
#include<algorithm>
#include<functional>
#define inf 1e9
#define ll long long
#define pii pair<int,int>
using namespace std;
const int N = 1e4+10;
int t, n, m, k;
ll len[N], sum[N];
int cnt;
//2^n * (n-1)+2
void init(){
ll cnt = 2;
for(int i = 1;i <= 29;i++){
len[i] = cnt*(i-1)+2;
cnt*=2;
}
// for(int i = 1;i <= 29;i++){
// cout<<i<<" "<<len[i]<<"\n";
// }
}
void solve(){
cin>>k;
if(k==1)cout<<"0\n";
else{
int pos = lower_bound(len+1,len+30,k)-len;
// cout<<pos<<"___\n";
if(len[pos]==k){
cout<<pos<<"\n";
}
else{
cout<<pos<<"\n";
}
}
}
int main(){
init();
cin>>t;
// t = 1;
while(t--)
solve();
return 0;
}
