基本概念
| 概念 | 含义 |
|---|---|
| 数据 | 所有能输入到计算机中的描述客观事物的符号,如文本、声音、图像、符号等 |
| 数据元素 | 数据的基本单位,也称节点或记录 |
| 数据项 | 有独立含义的数据最小单位,也称域。若干个数据项构成数据元素,数据项是不可分割的最小单位 |
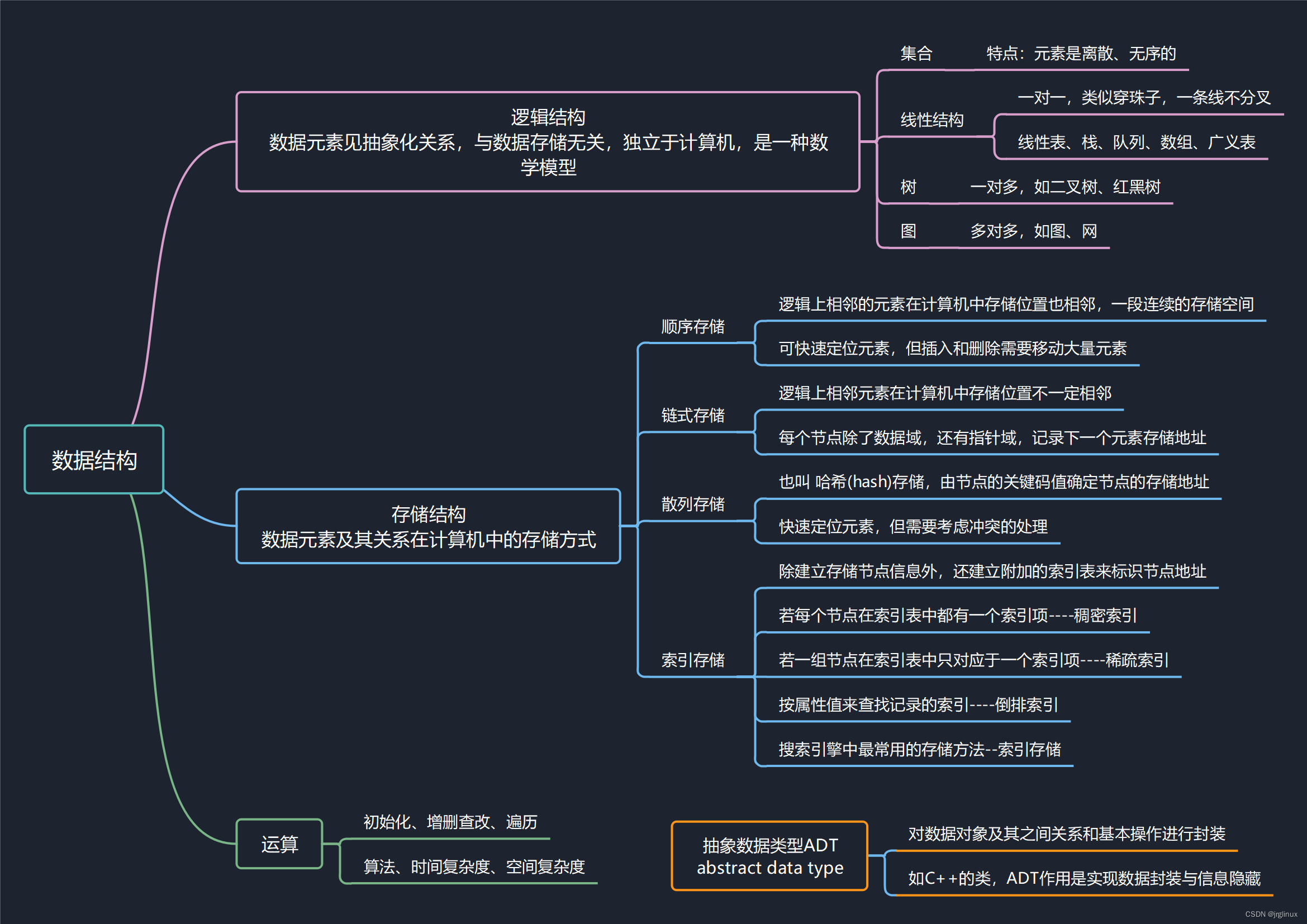
| 数据结构 | 相互之间存在一种或多种特定关系的数据元素的集合,包含逻辑结构、存储结构、运算三个要素 |
数据结构包含的基本概念整理如下图所示。
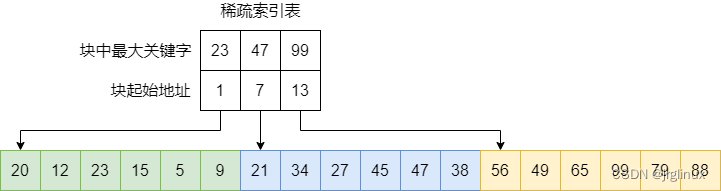
稀疏索引表示例:
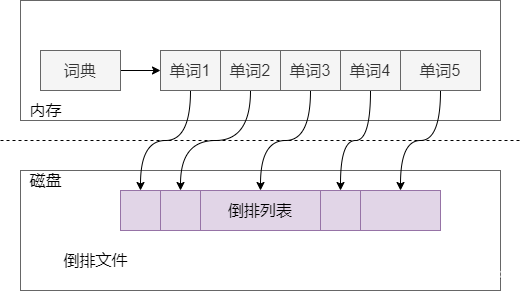
倒排索引示例:
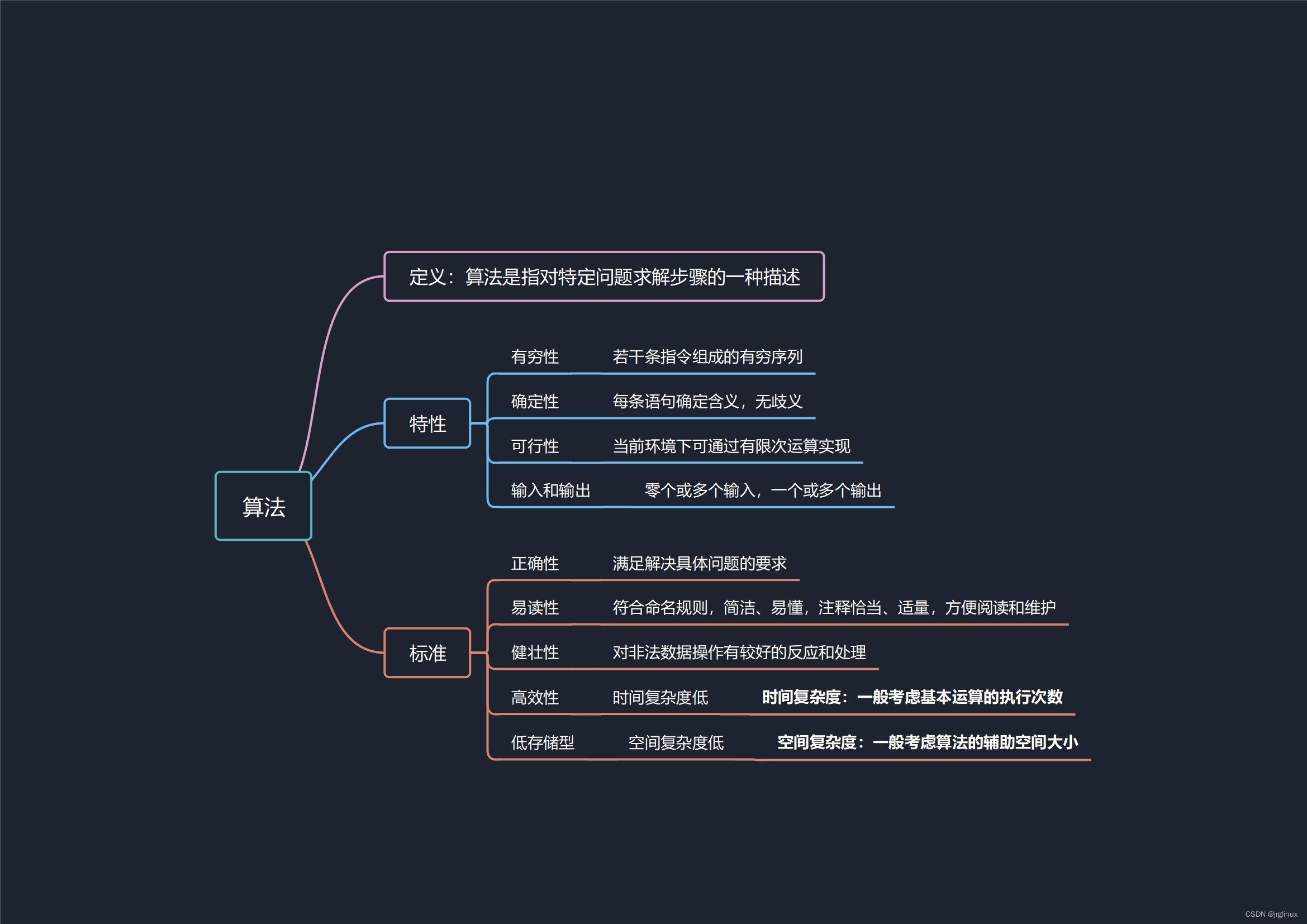
算法
算法是指对特定问题求解步骤的一种描述。
时间复杂度
时间复杂度:算法运行需要的时间,一般将算法基本运行的执行次数作为时间复杂度的度量标准。
示例1:
sum = 0; //运行1次
total = 0; //运行1次
for(i = 0; i < n; i++){ //运行n+1次,最后一次判断不成立,结束
sum += i; //运行n次
for(j = 0; j < n; j++) //运行n*(n+1)次
total += i*j; //运行n*n次
}
总共运行次数:1+1+(n+1)+n+n*(n+1)+n*n = 2n^2 +3n+3,当n足够大时,算法运行次数主要取决于高项,其余可忽略不计。**O(f(n)) = O(n2)**,用**O(n2)**表示示例1的时间复杂度。
示例2:
i = 1; //运行1次
while(i <= n){ //运行log2(n)次
i = i*2; //运行log2(n)次
}
总共运行次数:1+2log2(n),时间复杂度记为O(log2(n))。计算机中logn默认就是以2为底的幂函数。
示例3:
int findx(int x){ //在数组a[n]中顺序查找x
for(i = 0; i < n; i++){
if(a[i] == x)
return i;
}
return -1;
}
该程序很难计算到底执行了多少次,因为执行次数依赖于x在数组中的位置。
最好情况:第一个元素就是x,则执行1次;最坏情况:最后一个元素是x,执行n次;平均情况:如果分布概率均等,则平均执行次数为(n+1)/2次。
有些算法可以分最好情况、最坏情况、平均情况来求解时间复杂度,我们一般要考虑到最坏情况,才有实际参考意义。
空间复杂度
算法占用空间的大小,一般将算法的辅助空间作为衡量标准。
一个算法占用的空间:
- 输入输出数据所占空间
- 算法本身所占空间
- 额外需要的辅助空间
示例1:
swap(int x, int y){
int tmp;
tmp = x; //tmp为辅助空间
x = y;
y = tmp;
}
该算法使用了一个辅助空间,因此空间复杂度为O(1)。
示例2:
fac(int n){ //计算n的阶乘
if(n<0){
printf("n<0, data error");
return -1;
}
else if(n == 0 || n == 1)
return 1;
else
return n*fac(n-1);
}
递归算法中,每一次递推需要一个栈空间来保存调用记录,因此空间复杂度需要计算递归栈的辅助空间。
该计算n的阶乘程序中,每次需要进栈压栈,到最后出栈。空间复杂度是O(n),时间复杂度是O(n)。
时间复杂度的优劣:
**O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n) **
斐波那契问题
了解下快速幂法:如何快速的求解A的B次方,可以参考这篇博文。
斐波那契数列:1,1,2,3,5,8,13,21,34,55…
/*fibonacci: 1 1 2 3 5 8 13 21 ...*/
#include "stdio.h"
#include "sys/time.h"
#include "string.h"
#include "time.h"
/*递归法, O((3/2)^n)*/
int fibo1(int n){
if(n < 1)
return 0;
if(n == 1 || n == 2)
return 1;
else
return fibo1(n-1) + fibo1(n-2);
}
/*迭代法, O(n)*/
int fibo2(int n){
int x = 1, y = 1;
int i = 0;
if(n < 1)
return 0;
for(i = 2; i < n; i++){
y = x + y;
x = y - x;
}
return y;
}
/*矩阵快速幂法, O(logn)
* |1,1|(n-1)
* F(n) = | | * F(1)
* |1,0|
*/
void multiply(int F[2][2], int M[2][2]){
int a = F[0][0] * M[0][0] + F[0][1]*M[1][0];
int b = F[0][0] * M[0][1] + F[0][1]*M[1][1];
int c = F[1][0] * M[0][0] + F[1][1]*M[1][0];
int d = F[1][0] * M[0][1] + F[1][1]*M[1][1];
F[0][0] = a;
F[0][1] = b;
F[1][0] = c;
F[1][1] = d;
}
void power(int F[2][2], int n){
if(n < 2)
return;
int M[2][2] = {{1,1},{1,0}};
power(F, n/2);
multiply(F, F);
if( n & 1)
multiply(F, M);
}
int fibo3(int n){
int F[2][2] = {{1,1},{1,0}};
if(!n)
return 0;
power(F, n-1);
return F[0][0];
}
int main(int argc, char *argv[]){
int n = 0;
unsigned int Fn = 0;
clock_t start, end;
printf("input number:\n");
scanf("%d", &n);
start = clock();
Fn = fibo1(n);
end = clock();
printf("fibo1, f(%d):%u, sec:%f\n", n, Fn, (double)(end - start)/CLOCKS_PER_SEC);
start = clock();
Fn = fibo2(n);
end = clock();
printf("fibo2, f(%d):%u, sec:%f\n", n, Fn, (double)(end - start)/CLOCKS_PER_SEC);
start = clock();
Fn = fibo3(n);
end = clock();
printf("fibo3, f(%d):%u, sec:%f\n", n, Fn, (double)(end - start)/CLOCKS_PER_SEC);
return 0;
}
