[数据结构与算法] 容积卡尔曼滤波算法 CKF

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 容积卡尔曼滤波算法 CKF -> 正文阅读

[数据结构与算法]容积卡尔曼滤波算法 CKF

容积卡尔曼仿真案例
一、状态模型：
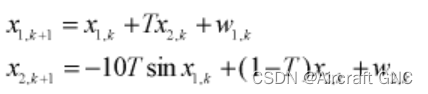
在这里插入图片描述
二、测量模型：

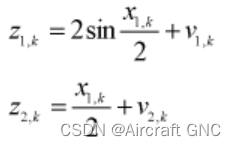
状态方程和测量方程中的噪声均为期望为零的白噪声。
三、状态模型和测量模型的噪声矩阵及初始状态及协方差矩阵：

四、C++ 仿真源码：
CKF.h

#pragma once
#pragma once
#include <fstream>     
#include <string>   
#include <iostream>
#include <Eigen/Dense>
#include "RandomGenerate.h"

class CKF
{
public:
	CKF();
	virtual ~CKF();
	void Filter();                // 容积卡尔曼滤波主函数

private:
	void Initialize();                                                                                     // 初始化相关参数
	void GenerateRealx(double h);                                                                          // 生成状态向量真实值
	void GenerateRealz();																				   // 生成测量向量值

	Eigen::MatrixXd GenerateCubaPoint(const Eigen::Matrix2d& PestChol);                                    // 生成容积点
	Eigen::MatrixXd Nonlinearf(double h, const Eigen::MatrixXd& CubaPointest);                             // 非线性状态方程(非线性映射)
	void Prediction(const Eigen::MatrixXd& CubaPointpre);                                                  // 一步预测

	Eigen::MatrixXd GenerateCubaPoint2(const Eigen::Matrix2d& PpreChol);                                   // 生成容积点
	Eigen::MatrixXd Nonlinearh(const Eigen::MatrixXd& CubaPointz_pre);                                     // 非线性测量方程
	void Update(const Eigen::MatrixXd& CubaPointz_pre, const Eigen::MatrixXd& CubaPointz);                 // 测量更新

private:
	int n;

	double gama;

	Eigen::VectorXd Wm;

	Eigen::Vector2d xpre;          // 状态向量预测值

	Eigen::Matrix2d Ppre;          // 状态协方差矩阵预测值

	Eigen::Matrix2d Q;             // 状态方程噪声矩阵

	Eigen::Matrix2d R;             // 测量方程噪声矩阵

	Eigen::Matrix2d K;             // 卡尔曼增益矩阵

	Eigen::Vector2d xest;          // 状态向量估计值

	Eigen::Matrix2d Pest;          // 状态协方差矩阵估计值

	Eigen::Vector2d xreal;

	Eigen::Vector2d zreal;

private:
	std::string FileName;          // 文件名

	std::ofstream outFile;         // 文件路径
};

CKF.cpp

#include "CKF.h"

CKF::CKF() : FileName("./FilterCKF.txt"), outFile(FileName, std::ios::out)
{
	// 初始化相关参数
	Initialize();
}
CKF::~CKF()
{

}

// 初始化相关参数
void CKF::Initialize()
{
	// 初始化状态方程噪声矩阵
	Q << 0.01, 0,
		0, 0.0001;

	// 初始化测量方程噪声矩阵
	R << 0.1, 0,
		0, 0.1;

	// 初始化状态协方差矩阵估计值
	Pest << 1, 0,
		0, 1;

	// 初始化状态向量估计值
	xest << 1, 0;

	// 真实值
	xreal = xest;

	// others
	n = 2;
	gama = sqrt(n / 2.0);

	// weight
	Eigen::VectorXd W0(4);
	W0 << 0, 0, 0, 0;
	Wm = W0;
	for (int i = 0; i != 4; i++)
	{
		Wm(i) = 1.0 / (2 * n);
	}

	return;
}

// 生成状态向量真实值
void CKF::GenerateRealx(double h)
{
	xreal(0) = xreal(0) + h * xreal(1) + sqrt(Q(0, 0)) * getRandom();
	xreal(1) = -10 * h * sin(xreal(0)) + (1 - h) * xreal(1) + sqrt(Q(1, 1)) * getRandom();
	return;
}

// 生成测量向量值
void CKF::GenerateRealz()
{
	zreal(0) = 2 * sin(xreal(0) / 2.0) + sqrt(R(0, 0)) * getRandom();;
	zreal(1) = 0.5 * xreal(0) + sqrt(R(1, 1)) * getRandom();
	return;
}

// 生成容积点
Eigen::MatrixXd CKF::GenerateCubaPoint(const Eigen::Matrix2d& PestChol)
{
	Eigen::MatrixXd CubaPointest(2, 4);
	CubaPointest.col(0) = xest + gama * PestChol.col(0);
	CubaPointest.col(1) = xest + gama * PestChol.col(1);
	CubaPointest.col(2) = xest - gama * PestChol.col(0);
	CubaPointest.col(3) = xest - gama * PestChol.col(1);

	return CubaPointest;
}

// 非线性状态方程(非线性映射)
Eigen::MatrixXd CKF::Nonlinearf(double h, const Eigen::MatrixXd& CubaPointest)
{
	Eigen::MatrixXd CubaPointpre(2, 4);
	for (int i = 0; i != 4; i++)
	{
		CubaPointpre(0, i) = CubaPointest(0, i) + h * CubaPointest(1, i);
		CubaPointpre(1, i) = -10 * h * sin(CubaPointest(0, i)) + (1 - h) * CubaPointest(1, i);
	}

	return CubaPointpre;
}

// 一步预测
void CKF::Prediction(const Eigen::MatrixXd& CubaPointpre)
{
	xpre = CubaPointpre * Wm;
	Eigen::Matrix2d Pxx;
	Pxx << 0, 0, 0, 0;
	for (int i = 0; i != 4; i++)
	{
		Eigen::Vector2d temp = CubaPointpre.col(i) - xpre;
		Eigen::MatrixXd tempmat(2, 1);
		for (int j = 0; j != temp.size(); j++)
		{
			tempmat(j, 0) = temp(j);
		}
		Eigen::Matrix2d mat = tempmat * tempmat.transpose();
		Pxx += Wm(i) * mat;
	}

	Ppre = Pxx + Q;
	return;
}

// 生成容积点
Eigen::MatrixXd CKF::GenerateCubaPoint2(const Eigen::Matrix2d& PpreChol)
{
	Eigen::MatrixXd CubaPointz_pre(2, 4);
	CubaPointz_pre.col(0) = xpre + gama * PpreChol.col(0);
	CubaPointz_pre.col(1) = xpre + gama * PpreChol.col(1);
	CubaPointz_pre.col(2) = xpre - gama * PpreChol.col(0);
	CubaPointz_pre.col(3) = xpre - gama * PpreChol.col(1);

	return CubaPointz_pre;
}

// 非线性测量方程
Eigen::MatrixXd CKF::Nonlinearh(const Eigen::MatrixXd& CubaPointz_pre)
{
	Eigen::MatrixXd CubaPointz(2, 4);
	for (int i = 0; i != 4; i++)
	{
		CubaPointz(0, i) = 2 * sin(0.5 * CubaPointz_pre(0, i));
		CubaPointz(1, i) = 0.5 * CubaPointz_pre(0, i);
	}

	return CubaPointz;
}

// 测量更新
void CKF::Update(const Eigen::MatrixXd& CubaPointz_pre, const Eigen::MatrixXd& CubaPointz)
{
	Eigen::Vector2d zpre = CubaPointz * Wm;
	Eigen::Matrix2d Pzz;
	Pzz << 0, 0, 0, 0;
	for (int i = 0; i != 4; i++)
	{
		Eigen::Vector2d temp = CubaPointz.col(i) - zpre;
		Eigen::MatrixXd tempmat(2, 1);
		for (int j = 0; j != temp.size(); j++)
		{
			tempmat(j, 0) = temp(j);
		}
		Eigen::Matrix2d mat = tempmat * tempmat.transpose();
		Pzz += Wm(i) * mat;
	}

	Eigen::Matrix2d Pvv = Pzz + R;
	Eigen::Matrix2d Pxz;
	Pxz << 0, 0, 0, 0;
	for (int i = 0; i != 4; i++)
	{
		Eigen::Vector2d temp1 = CubaPointz_pre.col(i) - xpre;
		Eigen::Vector2d temp2 = CubaPointz.col(i) - zpre;
		Eigen::MatrixXd temp1mat(2, 1);
		Eigen::MatrixXd temp2mat(2, 1);
		for (int j = 0; j != temp1.size(); j++)
		{
			temp1mat(j, 0) = temp1(j);
			temp2mat(j, 0) = temp2(j);
		}
		Eigen::Matrix2d mat = temp1mat * temp2mat.transpose();
		Pxz += Wm(i) * mat;
	}

	K = Pxz * Pvv.inverse();
	xest = xpre + (K * (zreal - zpre));
	Pest = Ppre - (K * Pvv * K.transpose());
	return;
}

// 容积卡尔曼滤波主函数
void CKF::Filter()
{
	std::cout << "请输入滤波时间：" << std::endl;
	double time;
	std::cin >> time;
	double h = 0.05;
	int num = int(time / h);

	for (int i = 0; i != num; i++)
	{
		// 生成状态向量真实值
		GenerateRealx(h);

		// 生成测量向量值
		GenerateRealz();

		// 矩阵下三角分解
		Eigen::Matrix2d PestChol = Pest.llt().matrixL();

		// 生成容积点
		Eigen::MatrixXd CubaPointest = GenerateCubaPoint(PestChol);

		// 容积点点经过非线性状态方程(非线性映射)
		Eigen::MatrixXd CubaPointpre = Nonlinearf(h, CubaPointest);

		// 一步预测
		Prediction(CubaPointpre);

		// 矩阵下三角分解
		Eigen::Matrix2d PpreChol = Ppre.llt().matrixL();

		// 生成容积点
		Eigen::MatrixXd CubaPointz_pre = GenerateCubaPoint2(PpreChol);

		// 容积点经过非线性测量方程
		Eigen::MatrixXd CubaPointz = Nonlinearh(CubaPointz_pre);

		// 测量更新
		Update(CubaPointz_pre, CubaPointz);

		// 保存到文件
		outFile << xreal(0) << ", " << xreal(1) << ", " << xest(0) << ", " << xest(1) << ", " << xpre(0) << ", " << xpre(1) << std::endl;

		// 输出到控制台
		std::cout<< i <<":  " << abs(xreal(0)-xest(0)) << ", " << abs(xreal(1) - xest(1)) << std::endl;
	}
	return;
}

demo.cpp

#include "EKF.h"
#include "UKF.h"
#include "CKF.h"

int main()
{
	EKF ekf;
	//ekf.Filter();

	UKF ukf;
	//ukf.Filter();

	CKF ckf;
	ckf.Filter();

	system("pause");
	return 0;
}

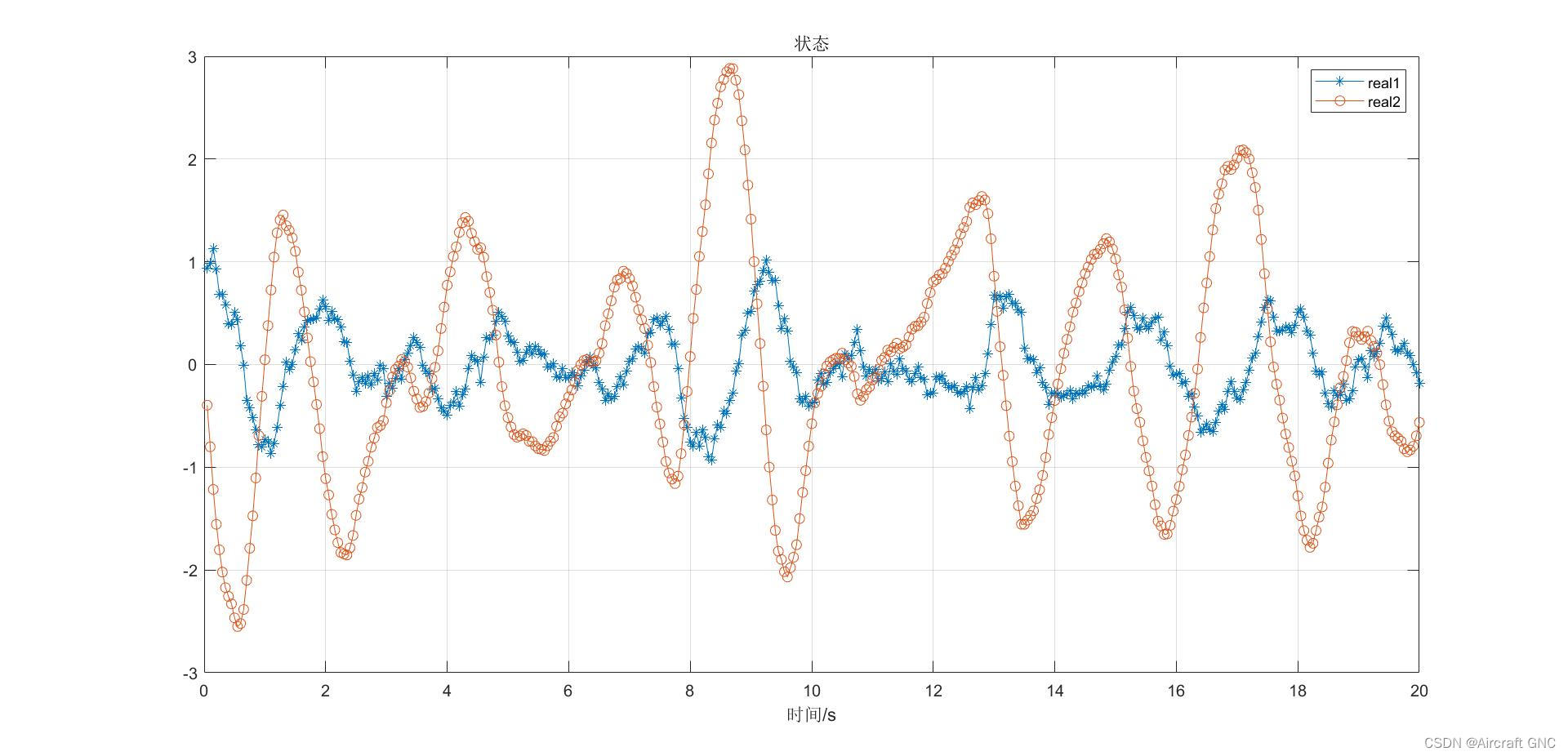
五、仿真结果：

%% 测试 C++ 程序的可行性。
clear;
clc;

%% 读入C++数据
x = dlmread('FilterCKF.txt');
n = length(x(:,1));
t = 1 : n;

%% 状态
figure;
plot(t, x(:,1), '*-');
hold on;
plot(t, x(:,2), 'o-');
legend('real1','real2');
title('状态');
xlabel('时间/s');
grid on;

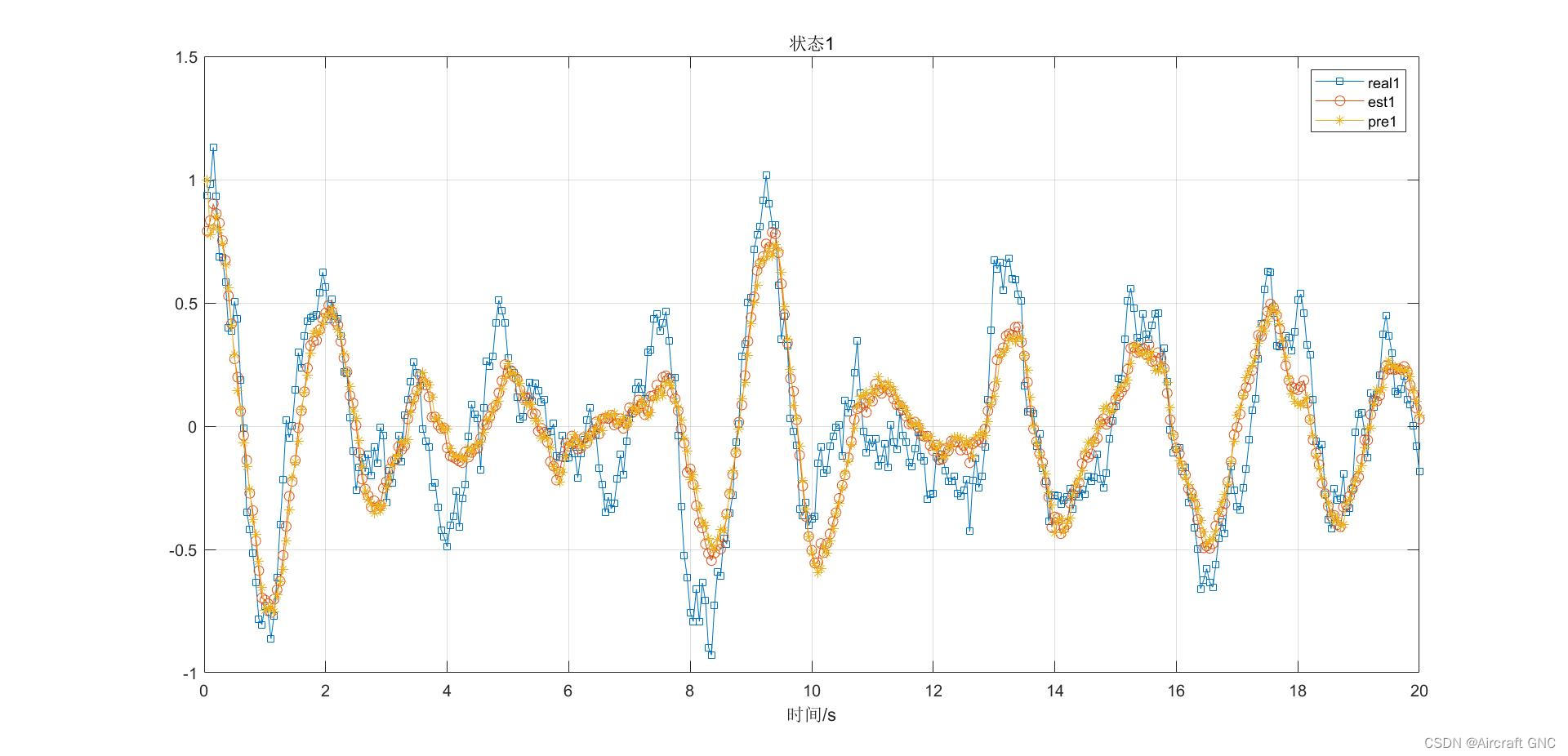
%% 状态1
figure;
plot(t, x(:,1), 's-', t, x(:,3), 'o-', t, x(:,5),'*-');
legend('real1','est1','pre1');
title('状态1');
xlabel('时间/s');
grid on;

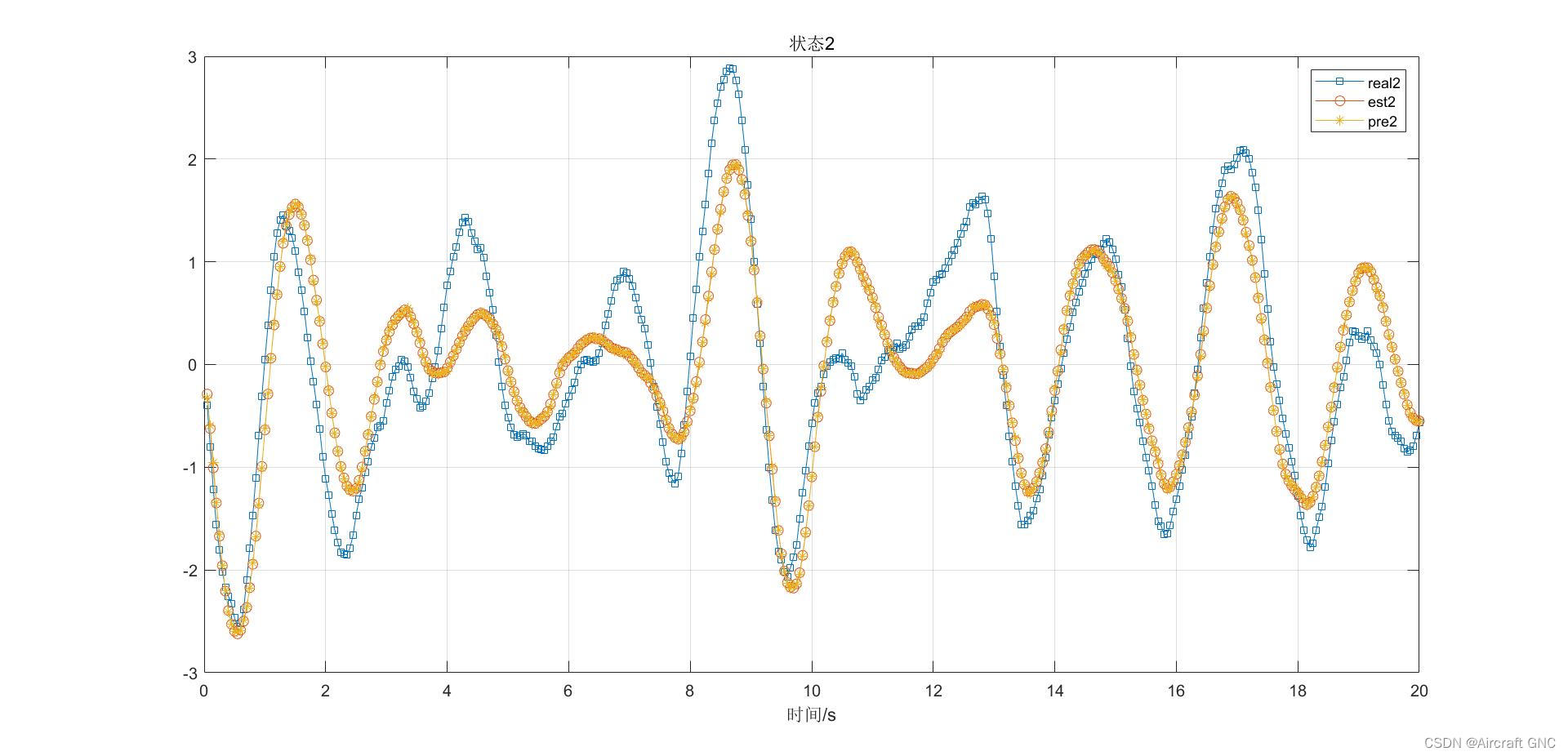
%% 状态2
figure;
plot(t, x(:,2), 's-', t, x(:,4), 'o-', t, x(:,6),'*-');
legend('real2','est2','pre2');
title('状态2');
xlabel('时间/s');
grid on;

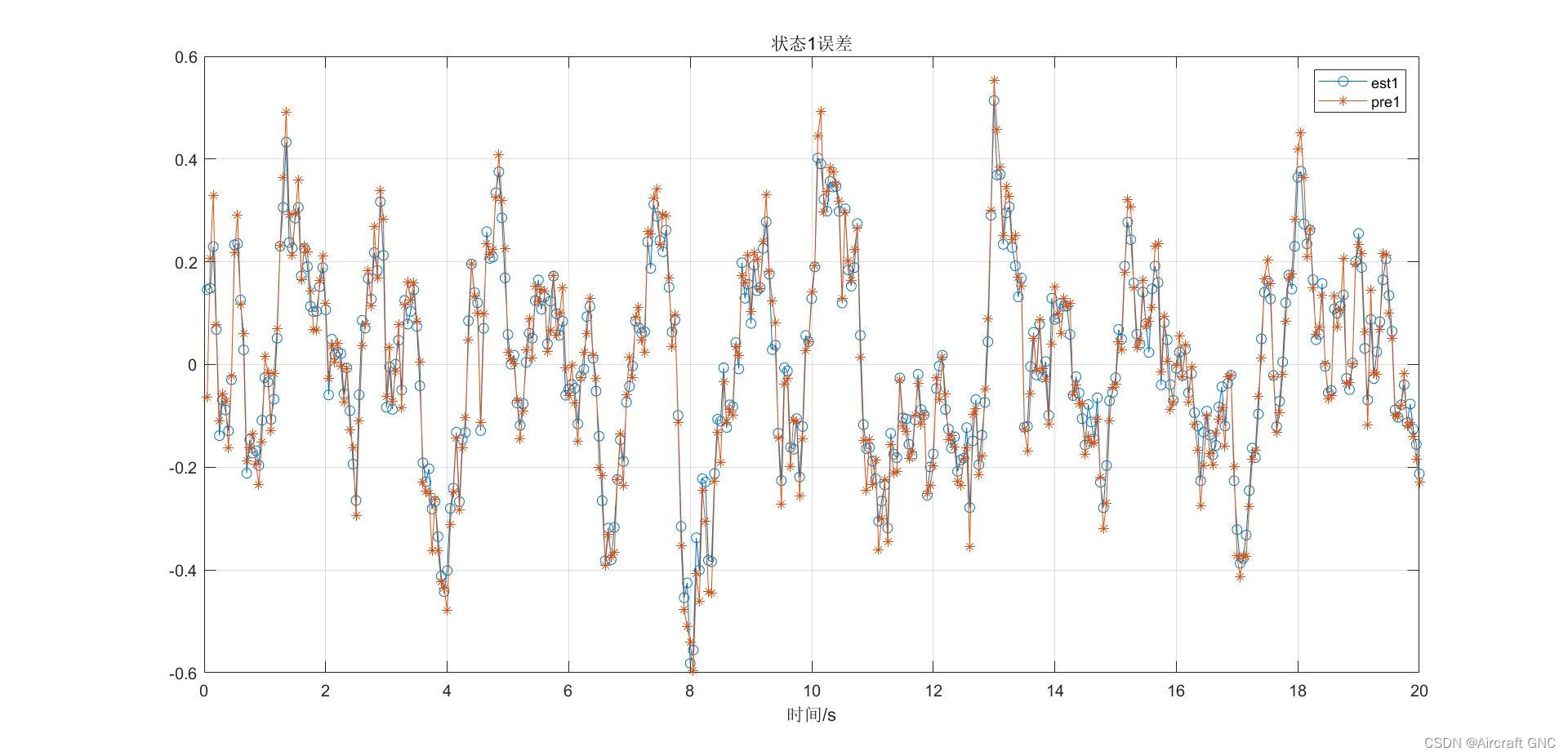
%% 状态1误差
figure;
plot(t, x(:,1)-x(:,3), 'o-', t, x(:,1)-x(:,5),'*-');
legend('est1','pre1');
title('状态1误差');
xlabel('时间/s');
grid on;

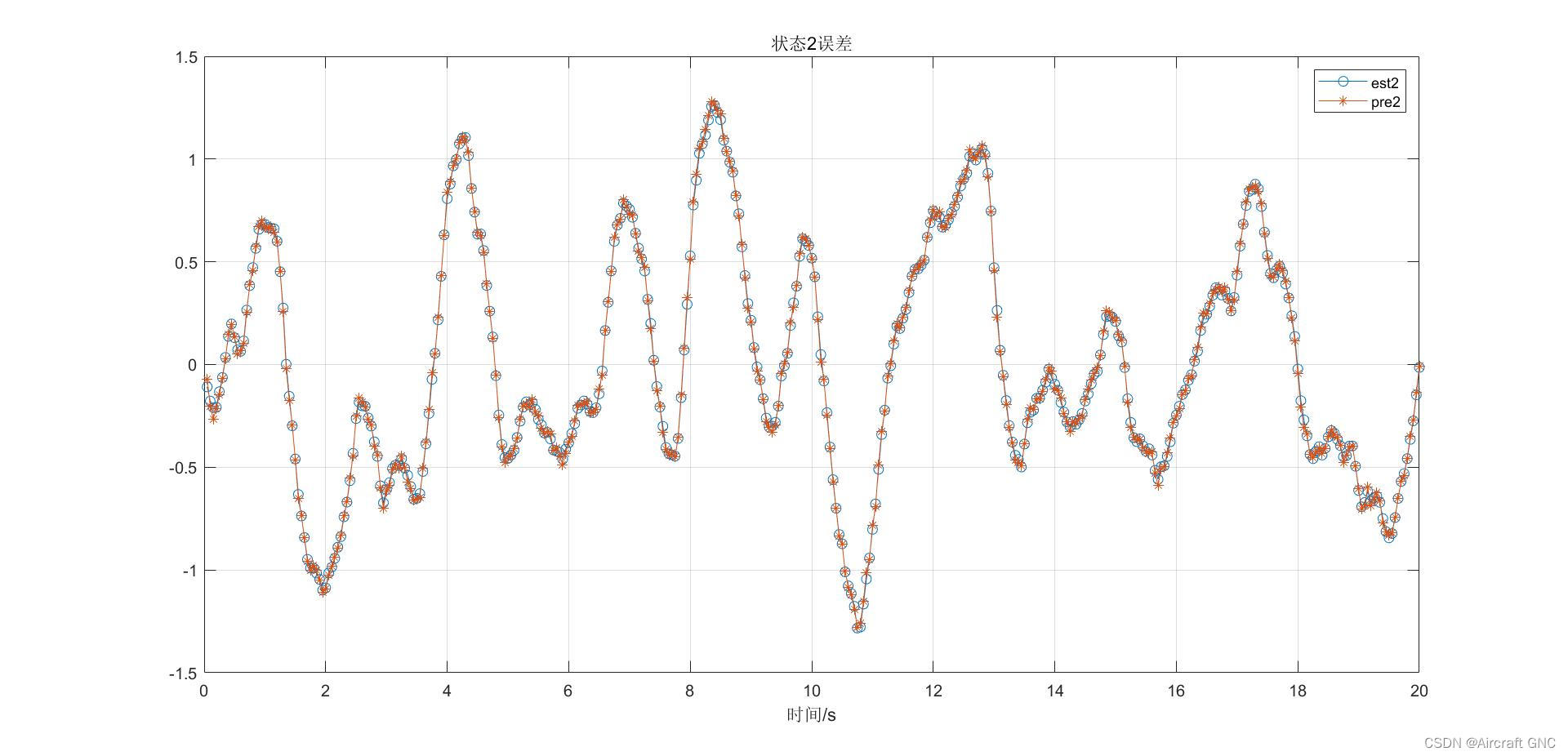
%% 状态2误差
figure;
plot(t, x(:,2)-x(:,4), 'o-', t, x(:,2)-x(:,6),'*-');
legend('est2','pre2');
title('状态2误差');
xlabel('时间/s');
grid on;