算法设计与分析复习
1.绪论
1.1算法特征及性质
| 特征 | 含义 |
|---|---|
| 输入(input) | 一个算法可以有零个或多个输入。 |
| 输出(output) | 一个算法应有一个或多个输出,作为算法进行信息加工的结果。 |
| 确定性(definiteness) | 确定性指算法中的每一个步骤都必须是有明确定义的。 |
| 可行性(effectiveness) | 算法中所有的操作都必须足够基本,使算法的执行者或阅读者明确其含义以及如何执行。 |
| 有穷性(finiteness) | 算法的有穷性是指算法必须总能在执行有限步骤之后终止。 |
| 满足目标/评价算法基本原则 |
|---|
| 正确性 |
| 可使用性 |
| 可读性 |
| 健壮性 |
| 高效率与低存储量需求 |
1.2时间复杂度分析
算法的复杂度主要包括时间复杂度和空间复杂度.
算法的时间复杂度指算法运行所需时间,也指执行算法所需要的计算工作量。
算法复杂性在渐近意义下的记号有:O、Ω、?等,分别表达运行时间的上界、运行时间的下界、运行时间的准确界等.
O上界
设函数f(n)和g(n)是定义在非负整数集合上的正函数,如果存在正整数n0和正常数c,使得当n≥n0时,有f(n)≤cg(n),就称f(n)的阶至多是O(g(n)),记做f(n) = O(g(n)),称为大O记号



?下界
设有函数f(n)和g(n)是定义在非负整数集合上的正函数,如果存在正整数n0和正常数c,使得当n≥n0时,有f(n)≥cg(n),就称f(n)的阶至少是?(g(n)),记做f(n) = ?(g(n)),称为?记号


Θ准确界
设有函数f(n)和g(n)是定义在非负整数集合上的正函数,如果存在正整数n0和正常数c1和c2(c1 ≤c2),使得当n≥n0时,
有c1 g(n)≤f(n)≤c2 g(n) ,就称f(n)的阶是Θ(g(n)),则记做f(n)=Θ(g(n)),称为Θ记号


1.3各个算法的时间复杂度
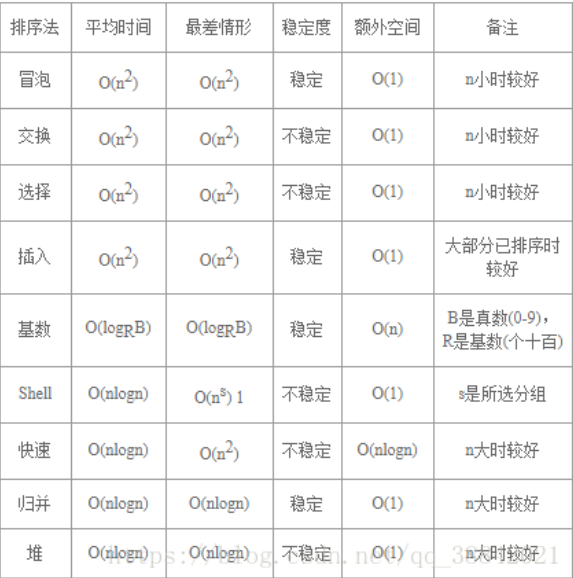
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡 | O(n2) | O(n2) | 稳定 | O(1) | n小时较好 |
| 选择 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(logRB) | O(logRB) | 稳定 | O(n) | B是真数(0-9),R是基数(个十百) |
| Shell | O(nlogn) | O(ns) 1<s<2 | 不稳定 | O(1) | s是所选分组 |
| 快速 | O(nlogn) | O(n2) | 不稳定 | O(nlogn) | n大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n大时较好 |
时间复杂度分类

2.递归
2.1递归方程的求解方法
设序列a0, a1, …, an, …, 简记为{an}, 一个把an与某些个ai(i<n)
联系起来的等式叫做关于序列 {an} 的递推方程
四种方法介绍
(1)迭代法:不断用递推方程的右部替换左部,有时候直接迭代可能不太方便,可以使用换元迭代。例如二分归并排序迭代方程的求解过程。
(2)差消法:差消法一般应用在递归方程右边不仅仅只依赖于当前项的前一项,而是前很多项,这种递归方程直接用迭代法很麻烦。属于高阶递归方程,因此要先把高阶递归方程进行差消,再进行迭代。例如快速排序的递归方程求解过程。
(3)递归树:建立递归树,每次迭代将函数项作为儿子,非函数项作为根的值。
(4)主定理法:
? 迭代法
? 直接迭代:插入排序最坏情况下时间分析
? 换元迭代:二分归并排序最坏情况下时间分析
? 差消迭代:快速排序平均情况下的时间分析
? 迭代模型:递归树
? 尝试法:快速排序平均情况下的时间分析
? 主定理:递归算法的分析
一、迭代法
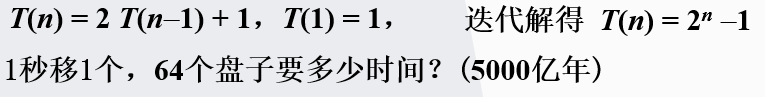




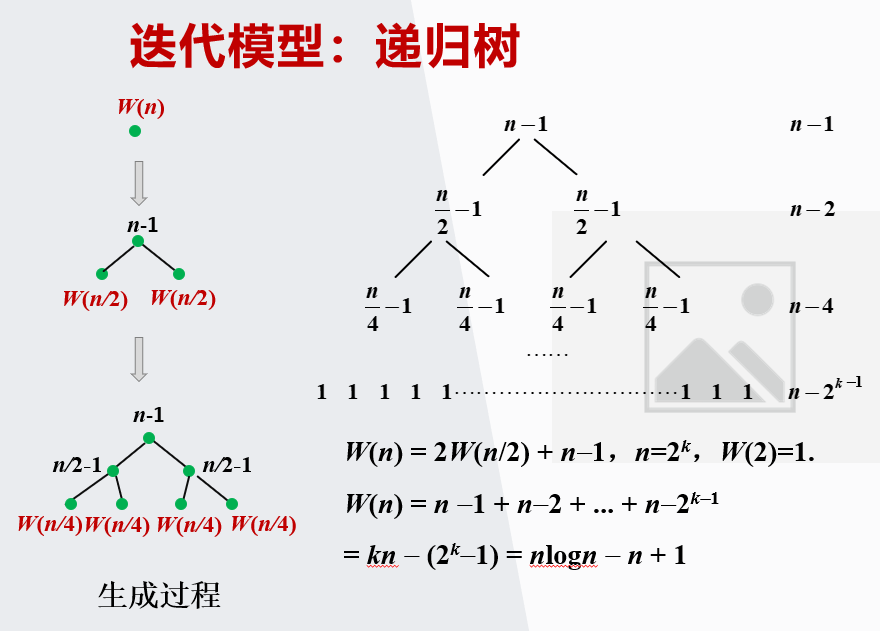
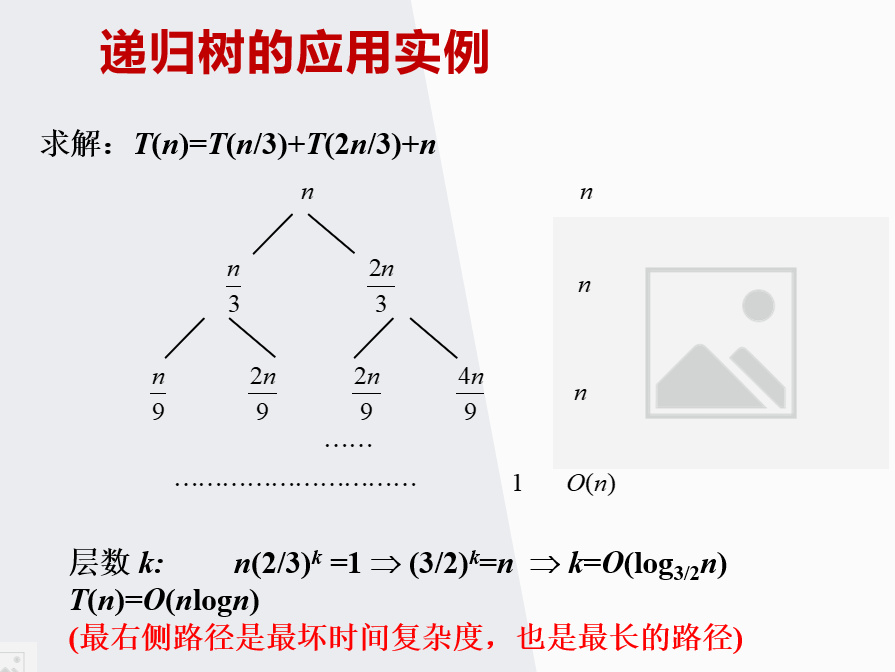
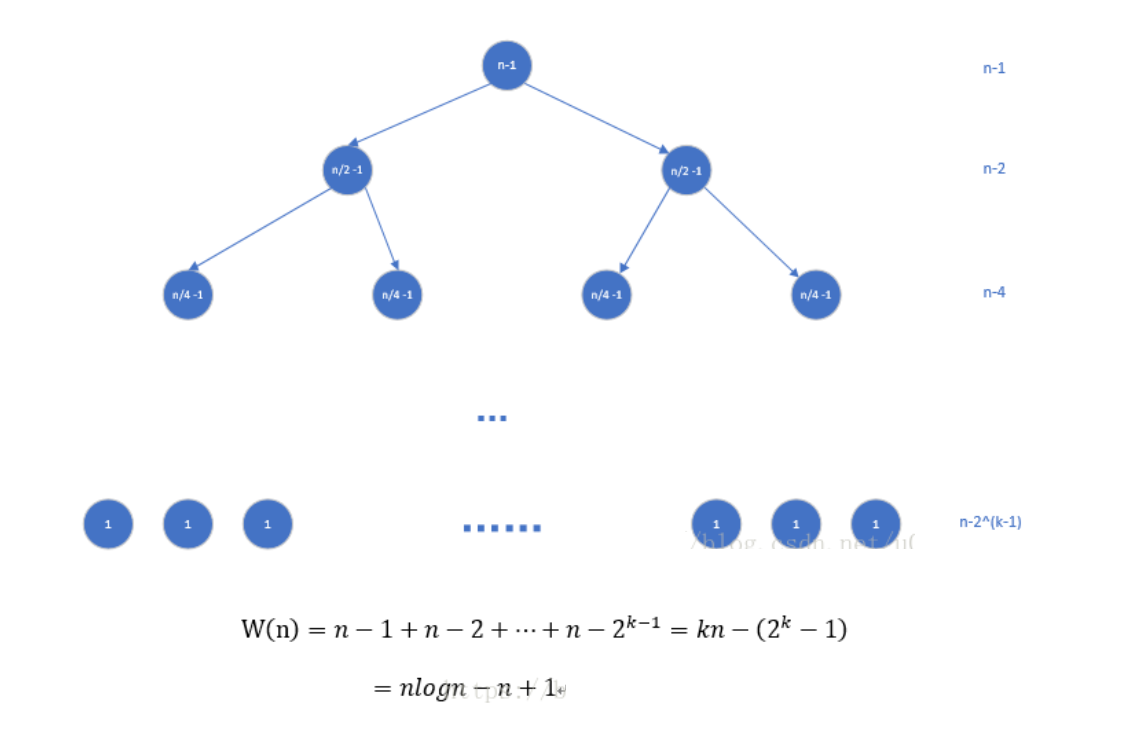
二、迭代树
树根:递归方程右侧除了函数外的剩余表达式
树叶:方程右侧的一个递归的函数项
最后所有结点的全之和就是W(n)
三、主定理





四、线性齐次方程求解
3.各类算法的基本思想和解题步骤
快速排序
快速排序的基本思想:
快速排序使用分治的思想,通过一趟排序将待排序列分割成两部分,其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序,以达到整个序列有序的目的。
快速排序的三个步骤:
(1)选择基准:在待排序列中,按照某种方式挑出一个元素,作为 “基准”(pivot)
(2)分割操作:以该基准在序列中的实际位置,把序列分成两个子序列。此时,在基准左边的元素都比该基准小,在基准右边的元素都比基准大
(3)递归地对两个序列进行快速排序,直到序列为空或者只有一个元素。
一、分治法
基本思想:
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。即一种分目标完成程序算法,简单问题可用二分法完成
解题步骤:
- 分解成若干个子问题
- 求解子问题
- 合并子问题
二、蛮力法
三、回溯法
基本思想:
确定了解空间的组织结构后,回溯法从根节点出发,以深度优先搜索方式搜索整个解空间。回溯法以这种工作方式递归地在解空间中搜索,直到找到所要求的解或解空间所有解都被遍历过为止。
回溯法又称试探法。回溯法的基本做法是深度优先搜索,是一种组织得井井有条的、能避免不必要重复搜索的穷举式搜索算法。回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
解题步骤:
(1)针对所给问题,定义问题的解空间;
(2)确定易于搜索的解空间结构;
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
四、贪心法
基本思想:
对问题求解时总是做出在当前看来是最好的选择,即不从整体最优上加以考虑,只做某种意义上的局部最优解
希望通过局部最优决策导致问题的全局最优解
贪心法的当前选择可能要依赖已经做出的所有选择,但不依赖于有待于做出的选择和子问题。因此贪心法自顶向下,一步一步地做出贪心选择。
求解步骤:
- 建立数学模型来描述问题
- 把求解的问题分成若干个子问题
- 对每一个子问题求解,得到子问题的局部最优解
- 把子问题的局部最优解合成原来解问题的一个解
五、动态规划
基本思想:
把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系逐个击破

解题步骤:
- 找出最优解的性质,并刻划其结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息,构造最优解
三个性质:
1.最优性原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优性原理。
2.无后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。
9)]
解题步骤:
- 找出最优解的性质,并刻划其结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息,构造最优解
三个性质:
1.最优性原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优性原理。
2.无后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。
3.有重叠子问题:即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)。
