
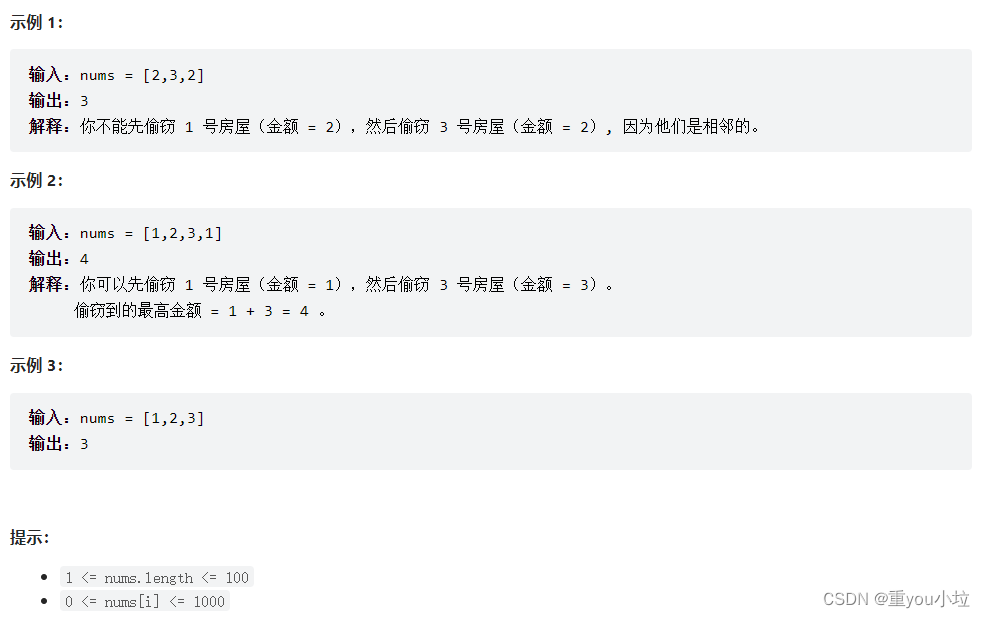
思路:dp
难点:环怎么破?
偷第一间,则不能偷最后一间,也就是 [0,n-2]中打家劫舍的模板
不偷第一间,则可以偷最后一间,也就是 [1,n-1]中打家劫舍的模板
因此状态转移跟打家劫舍一模一样
dp[i][0]表示不盗nums[i]的前提下前i所能偷盗的最大金额
dp[i][1]表示盗nums[i]的前提下前i所能偷盗的最大金额
转移方程如下:
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);
dp[i][1] = dp[i - 1][0] + nums[i]; 由前一个状态即可得到
边界:dp[0][0]=0 dp[0][1]=nums[0]
class Solution {
public:
int f(const vector<int>& nums) {
int n = nums.size();
int _0 = 0, _1 = nums[0];
for (int i = 1; i < n; ++i) {
int tmp1 = max(_0, _1);
int tmp2 = _0 + nums[i];
_0 = tmp1;
_1 = tmp2;
}
return max(_0, _1);
}
int rob(vector<int>& nums) {
int n = nums.size();
if (n == 1) return nums[0];
if (n == 2) return max(nums[0], nums[1]);
return max(f(vector<int>(nums.begin(), nums.begin() + n - 1)),
f(vector<int>(nums.begin() + 1, nums.begin() + n)));
}
};
