
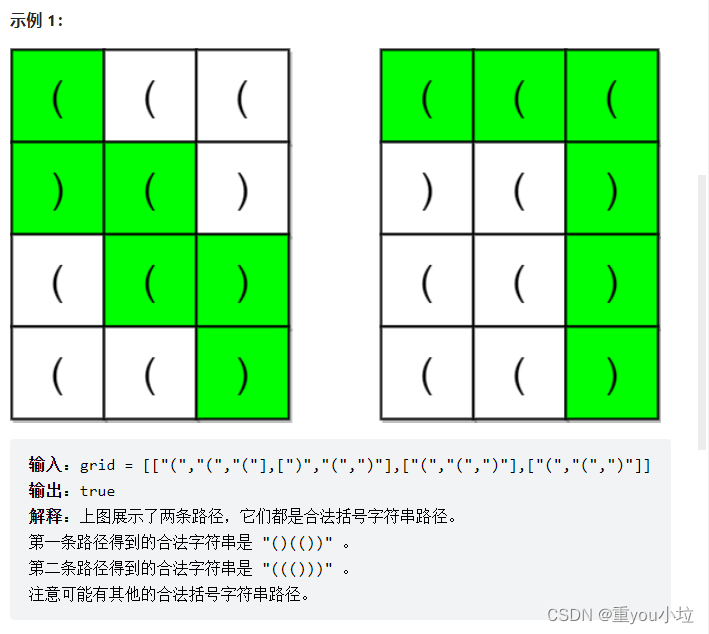

思路:记忆化dfs
知识点1:n * m的矩阵,向下需要走n-1次,向右需要走m-1次,加上[0][0]的位置,所以[0][0]到[n-1][m-1]经过的方格数为m-1+n(m-1+n-1+1)个
知识点2:遇到左括号加1,遇到右括号-1,由于左括号最多的个数为:(m-1+n)/2,所以在每个位置的状态为:0 ->(m-1+n)/ 2
时间复杂度分析:总共的状态数为:m * n * (m-1+n)/ 2,所以时间复杂度在O(10^6)
class Solution {
public:
bool vis[101][101][200];
unordered_map<char, int> hash;
bool dfs(vector<vector<char>>& grid, int x, int y, int val) {
int n = grid.size(), m = grid[0].size();
if (val < 0 || val > (n + m - x - y - 1)) return false; //剪枝
if (x == n - 1 && y == m - 1) { //递归终止
if (!val) return true;
else return false;
}
if (vis[x][y][val]) return false;//当再次来该点时,由于之前就不成立,所以直接return false
vis[x][y][val] = true; //第一次来的时候标记一下
return (y < m - 1 && dfs(grid, x, y + 1, val + hash[grid[x][y + 1]])) ||
(x < n - 1 && dfs(grid, x + 1, y, val + hash[grid[x + 1][y]]));
}
bool hasValidPath(vector<vector<char>>& grid) {
hash['('] = 1;
hash[')'] = -1;
int n = grid.size(), m = grid[0].size();
if ((m + n) % 2 == 0) return false;
if (grid[0][0] == ')' && grid[n - 1][m - 1] == '(') return false; //剪枝
memset(vis, 0, sizeof(vis));
return dfs(grid, 0, 0, hash[grid[0][0]]);
}
};
优化:判断合法括号序列剪枝的方法:
1:开始阶段:n为奇数
2:过程阶段(+1 -1):(1)剩余的个数<val,表示后面全是右括号都不匹配 (2)val小于0
