这三种排序都不是基于比较的排序,典型的空间换时间算法。
0. 修改父类
因为父类中针对稳定性判断时泛型的其它类,但是下方的排序只支持整数(浮点型等非自定义类型)。
/**
* 判断稳定性
* @return
*/
private boolean isStable(){
if (this instanceof CountingSortPro) return true;
if (this instanceof CountingSort) return true;
if (this instanceof ShellSort) return false;
if (this instanceof RadixSort) return true;
// 根据student类型测试,如果年龄相同的分数呈递增状态则是稳定性排序。
Student[] students = new Student[20];
for (int i = 0; i < students.length; i++) {
students[i] = new Student(i * 10, 10);
}
sort((T[]) students);
for (int i = 1; i < students.length; i++) {
int score = students[i].score;
int prevScore = students[i - 1].score;
if (score != prevScore + 10) return false;
}
return true;
}
1. 计数排序(Counting Sort)
1954年提出,适合对一定范围内的整数进行排序。
1.1 简单版本实现
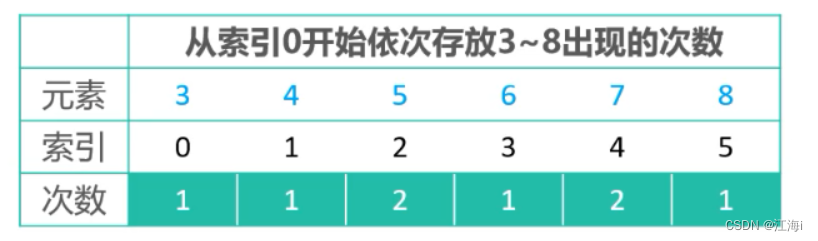
核心思想:统计每个整数在序列中出现的次数,进而推导每个整数在有序序列中的索引。
- 原数组

- 新建一个数组存储整数出现的次数:

- 推导结果:

/**
* @Description 计数排序实现
* @date 2022/5/8 15:05
*/
public class CountingSort extends Sort<Integer> {
@Override
protected void sort() {
// 获取数组最大值
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max){
max = arr[i];
}
}
// 开辟内存空间
int[] counts = new int[max + 1];
// 统计次数
for (int i = 0; i < arr.length; i++) {
counts[arr[i]]++;
}
// 根据出现的次数对整数进行排序
int index = 0;
for (int i = 0; i < counts.length; i++) {
while (counts[i] > 0) {
arr[index] = i;
index++;
counts[i]--;
}
}
}
}
1.2 优化思路
-
缺点:在上方1.1版本中存在以下问题:
- 不是稳定性排序;
- 消耗内存过大;
- 不能对负整数进行排序。
-
优化内存空间和负整数排序:获取最小值,将内存空间的大小从
[0,max]减少到[min,max];这种实现也达到了可以对负整数优化的目的,不再以元素值对应索引值,而是以顺序对应索引。得出结论:元素k在counts中的索引值为:k - min
-
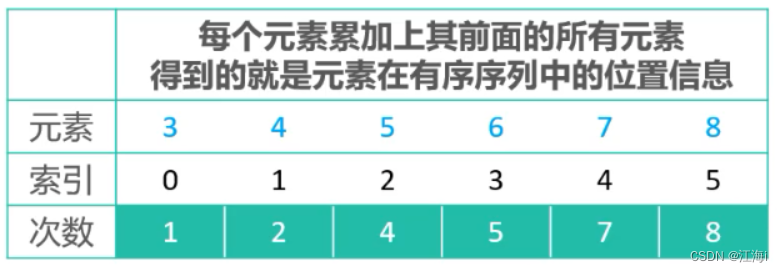
稳定性排序:每个次数加上前面所有元素出现的次数,可以得到当前元素在有序序列种的位置。

-
完成排序:得出结论:元素k在有序序列中的索引为:
counts[ k - min ] - p。p为倒数第几个k。
例如:索引为 6 的 7 是倒数第一个 7 ,在counts中的索引为:7 - 3 = 4;在有序序列中的索引为:7 - 1 = 6。

1.3 优化实现
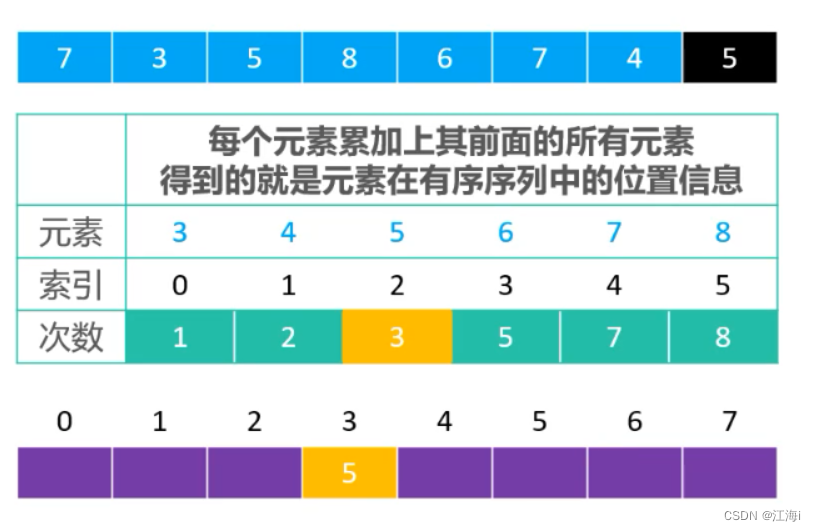
- 从后往前遍历:

- 使用相应的值计算出索引之后,下方
counts序列中也执行减一,这样可以做到稳定性。
- 然后将值放入到有序序列中:
/**
* @Description 优化版计数排序
* @date 2022/5/8 15:58
*/
public class CountingSortPro extends Sort<Integer> {
@Override
protected void sort() {
// 获取数组最大值
int max = arr[0];
int min = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max){
max = arr[i];
}
if (arr[i] < min){
min = arr[i];
}
}
// 开辟内存空间
int[] counts = new int[max - min + 1];
// 统计次数
for (Integer integer : arr) {
counts[integer - min]++;
}
// 统计累加的次数
for (int i = 1; i < counts.length; i++) {
counts[i] += counts[i - 1];
}
// 倒序遍历然后将值放到合适位置
int[] newArr = new int[arr.length];
for (int i = arr.length - 1; i >= 0; i--) {
// 将当前值根据在counts中的索引计算出新的位置。
// 先将值减一,在计算出当前值对应的索引
int index = --counts[arr[i] - min];
// 放到新序列中。
newArr[index] = arr[i];
}
// 覆盖序列
for (int i = 0; i < newArr.length; i++) {
arr[i] = newArr[i];
}
}
}
1.4 总结分析
- 时间复杂度:最好、最坏、平均:
O(n + k)。 - 空间复杂度:
O(n + k)。 - 属于稳定排序。
1.5 自定义对象实现计数排序
如果自定义的对象包含可共排序的整数类型,也可以使用计数排序。
- 自定义类:
/**
* @Description 自定义对象测试
* @date 2022/5/8 20:20
*/
@Data
@AllArgsConstructor
@ToString
public class Person {
private Integer id;
private String name;
}
- 计数排序:
/**
* @Description 自定义对象计数排序
* @date 2022/5/8 15:58
*/
public class CountingSortObj{
public static void main(String[] args) {
Person[] arr = {new Person(1,"aa")
,new Person(-1,"bb"),
new Person(99,"cc"),
new Person(5,"dd"),
new Person(0,"ee"),};
sort(arr);
for (Person person : arr) {
System.out.println(person);
}
}
private static void sort(Person[] arr) {
// 获取数组最大值
int max = arr[0].getId();
int min = arr[0].getId();
for (int i = 1; i < arr.length; i++) {
if (arr[i].getId() > max){
max = arr[i].getId();
}
if (arr[i].getId() < min){
min = arr[i].getId();
}
}
// 开辟内存空间
int[] counts = new int[max - min + 1];
// 统计次数
for (Person person : arr) {
counts[person.getId() - min]++;
}
// 统计累加的次数
for (int i = 1; i < counts.length; i++) {
counts[i] += counts[i - 1];
}
// 倒序遍历然后将值放到合适位置
Person[] newArr = new Person[arr.length];
for (int i = arr.length - 1; i >= 0; i--) {
// 将当前值根据在counts中的索引计算出新的位置。
// 先将值减一,在计算出当前值对应的索引
int index = --counts[arr[i].getId() - min];
// 放到新序列中。
newArr[index] = arr[i];
}
// 覆盖序列
System.arraycopy(newArr, 0, arr, 0, newArr.length);
}
}
2. 基数排序(Radix Sort)
非常适合用于整数排序,特别是非负整数。
2.1 执行流程
依次对个位数、十位数、百位数…进行排序(从低位到高位)。
- 原始数组

- 对个位数进行排序后

- 再对十位数进行排序,没有就为0

- 最后对百位数再进行排序:

2.2 实现
因为每次针对位数进行排序时,只有 0~9 ,非常符合使用计数排序。
所以这里整合计数排序进行实现。
/**
* @Description 基数排序
* @date 2022/5/8 20:37
*/
public class RadixSort extends Sort<Integer> {
@Override
protected void sort() {
// 获取数组最大值
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max){
max = arr[i];
}
}
// 计算基数
// 个位数 : x / 1 % 10
// 十位数 : x / 10 % 10
// 百位数 : x / 100 % 10
// 针对最大值的位数判断需要执行多少次计数排序
for (int divider = 1; divider <= max; divider *= 10) {
countingSort(divider);
}
}
/**
* 针对基数进行计数排序
* @param divider 被除数
*/
private void countingSort(int divider){
int[] counts = new int[10];
for (Integer integer : arr) {
counts[integer / divider % 10]++;
}
for (int i = 1; i < counts.length; i++) {
counts[i] += counts[i - 1];
}
int[] newArr = new int[arr.length];
for (int i = arr.length - 1; i >= 0; i--) {
int index = --counts[arr[i] / divider % 10];
newArr[index] = arr[i];
}
for (int i = 0; i < newArr.length; i++) {
arr[i] = newArr[i];
}
}
}
2.3 复杂度分析
- 最好、最坏、平均复杂度:
O(d * (n + k)),d是最大值的位数,k是进制数; - 空间复杂度:
O( n + k ),k是进制数; - 属于稳定排序。
3. 桶排序(Bucket Sort)
3.1 执行流程
- 创建一定数量的桶(数组、或者链表);
- 按照一定规则将序列中的元素均匀的分配到对应的桶;
- 分别对桶单独排序;
- 将所有的非空桶元素合并成有序序列。
-
对小数排序:因为小数全部的是小于一的,如果直接按照值放入到桶中都会放到索引为0 的桶中,这里乘以数组长度:

-
根据乘以 数组长度 之后的索引放到对应的桶中:
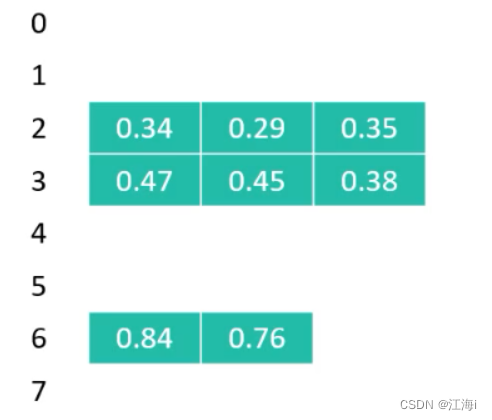
-
分别进行排序:
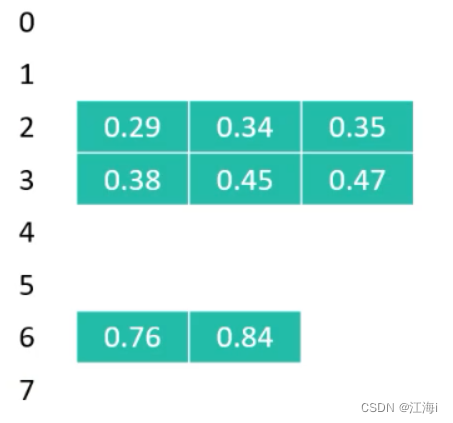
-
将所有元素统一进行排序:

3.2 实现
/**
* @Description 桶排序
* @date 2022/5/8 20:58
*/
public class BucketSort {
public static void main(String[] args) {
Double[] arr = {0.34, 0.47, 0.29, 0.84, 0.45, 0.38, 0.35, 0.76};
bucketSort(arr);
for (Double aDouble : arr) {
System.out.print(aDouble + "_");
}
}
public static void bucketSort(Double[] arr){
// 创建一个存放 double类型的list 的数组
List<Double>[] buckets = new List[arr.length];
// 遍历数组
for (Double info : arr) {
// 根据长度计算索引
int bucketIndex = (int) (info * arr.length);
// 将当前索引位置的数组赋值给list
List<Double> bucket = buckets[bucketIndex];
// 如果list为空,新建一个
if (bucket == null){
bucket = new LinkedList<>();
buckets[bucketIndex] = bucket;
}
// 将当前值存放到索引位置的链表中
bucket.add(info);
}
// 对每个桶进行排序
int index = 0;
// 遍历桶数组
for (List<Double> bucket : buckets) {
// 如果桶数组为空,不进行操作
if (bucket == null) continue;
// 调用JDK方法对当前桶进行排序
bucket.sort(null);
// 遍历当前桶,赋值给原先的序列
for (Double aDouble : bucket) {
arr[index++] = aDouble;
}
}
}
}
3.3 复杂度分析
- 空间复杂度:
O(n + m),m是桶的数量; - 时间复杂度:
O( n + k); - 属于稳定排序
