目录
二叉搜索树
之前我们提过普通二叉树价值不大,二叉树要叠加一些性质才能变的非常有价值。
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
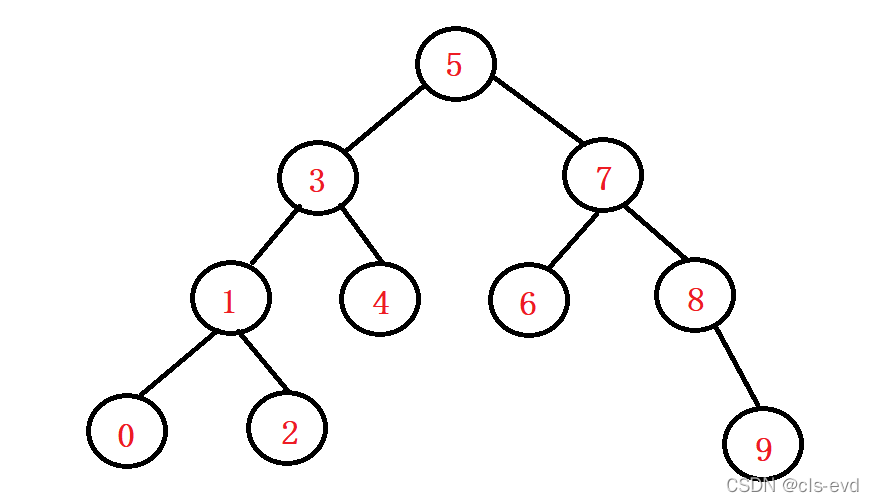
比如查6,比根大在右树去找,比7小在左树去找就找到了,一共三次。
最多查找高度次O(logN) (这是在不极端的情况下,能做到满二叉树或完全二叉树的情况) 。eg:10亿个数据最多只需要找30次。全国16亿人如果能将他们建成一个理想情况的二叉搜索树也仅仅需要31次。
但是实际情况不一定会这么理想,他也可能是下图这个样子。这种情况下就是个O(N)。

所以说搜索二叉树是不成熟的,后面就搞出来平衡搜索二叉树(AVLTree,RBTree)。
搜索二叉树中序遍历就是升序的一串数,所以他也叫二叉排序数。
二叉树的实现
定义搜索树的节点
template<class K>
//struct BinarySearchTreeNode
struct BSTteeNode //定义结点
{
BSTteeNode<K>* _left;
BSTteeNode<K>* _right;
K _key;
BSTteeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};定义二叉搜索树
只需要有个根节点即可
template<class K>
struct BSTree
{
typedef BSTteeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
private:
Node* _root;
};
(1)insert的实现
一般线性表喜欢叫push,非线性的就叫insert

代码实现:
bool Insert(const K& key)
{
//如果根为空
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr; //存储cur上一个位置
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else //数据重复返回假
{
return false;
}
}
//走到空了已经,考虑链接
cur = new Node(key);
//不知道应该链接到左边还是右边,在比较一次
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}为什么这有个返回值呢?
因为默认情况下搜索树是不允许冗余的,也就是这棵树已经有数据5了,当你还要插入数据5时就不允许你插入,返回false,不允许有重复的值。
我们写个中序遍历验证insert.注意这里的中序要嵌套这些=写,因为我们在类外面是拿不到_root的
void InOrder()
{
_InOrder(_root);
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}测试结果:代表我们的插入没有问题。
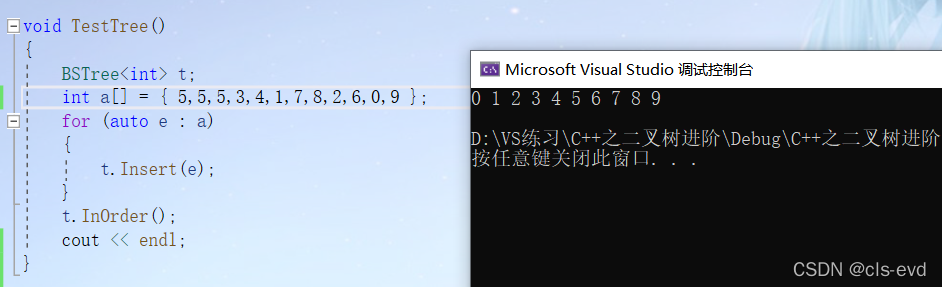
(2)Find
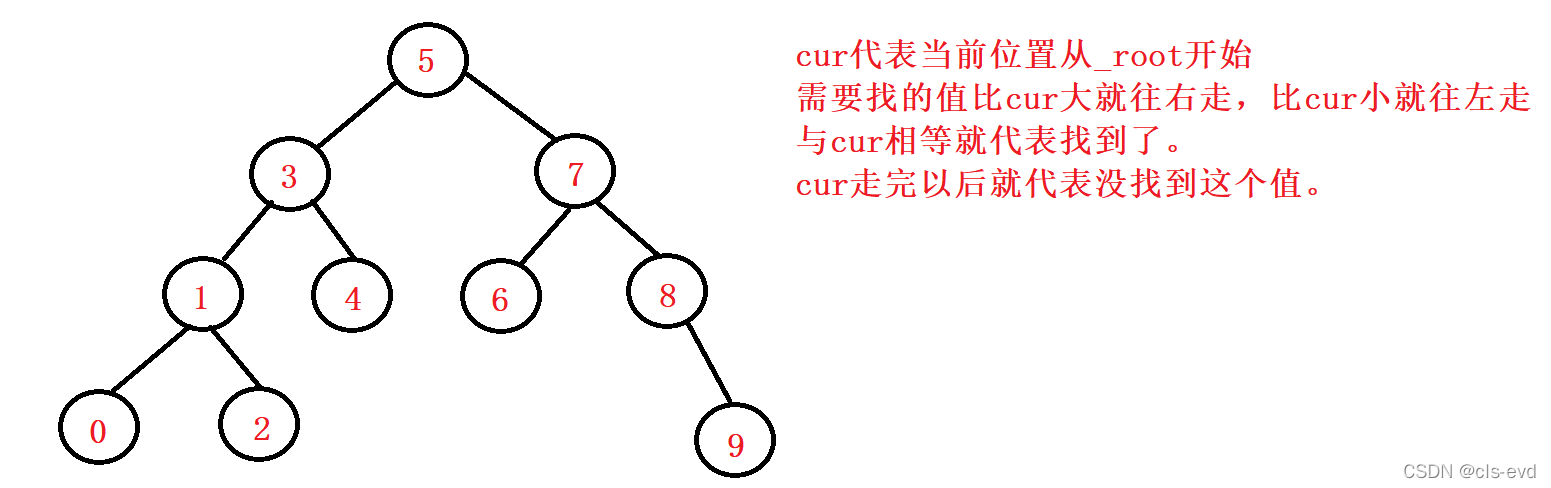
代码实现:
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}?测试结果:
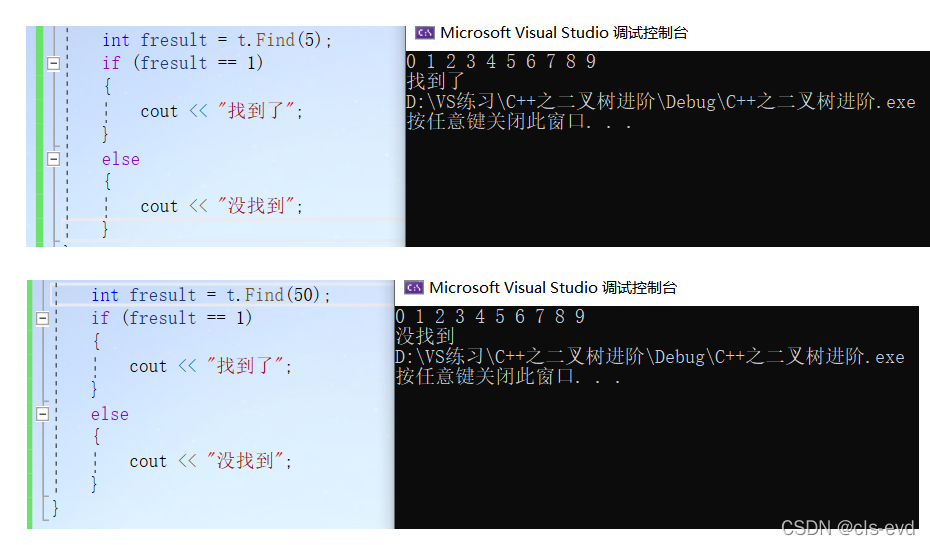
(3)Erase
1.0 删除2 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 把2干掉,将1的右置空。
2.0 删除8??????????????????????????????????????????????????????????????????????????????????????????????????????????????????? ? ? ? ? ? ? ? ? ? ? ? ? 8是左为空,将8干掉后,让8的父亲的右节点指向8的右节点。如果8是右为空,将8干掉后,让8的父亲的右节点指向8的左节点。??
3.0 删除5
? ? ? ? 5有两个孩子,利用替换法删除找一个值替换5,这个值应该做到比左边的大,比右边的小。这个值就应该是左子树的最由节点或者是右子树的最左节点,左子树的最大节点一定是右为空,右子树的最左节点一定是左为空。

代码实现:
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if(key<cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//找到了准备开始删除
//删除有一个孩子或者没有孩子的节点
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //删除有两个孩子的节点
{
//首先找替代节点
//替换节点:右子树的最左节点,
//这个节点的左孩子一定是空(他自己就是最左了),右孩子可能是空可能非空。
Node* minparent = cur;
Node* min = cur->_right;
while (min->_left)
{
minparent = min;
min = min->_left;
}
//找到之后覆盖要删除的节点。
cur->_key = min->_key;
//再将min删除
if (minparent->_left == min)
{
//因为是右子树的最左节点,所以一定是min的右孩子
minparent->_left = min->_right;
}
else
{
minparent->_right = min->_right;
}
delete min;
}
return true;
}
}
return false;
}删除有一个孩子或者没有孩子的节点:
???????cur的左为空的两种情况: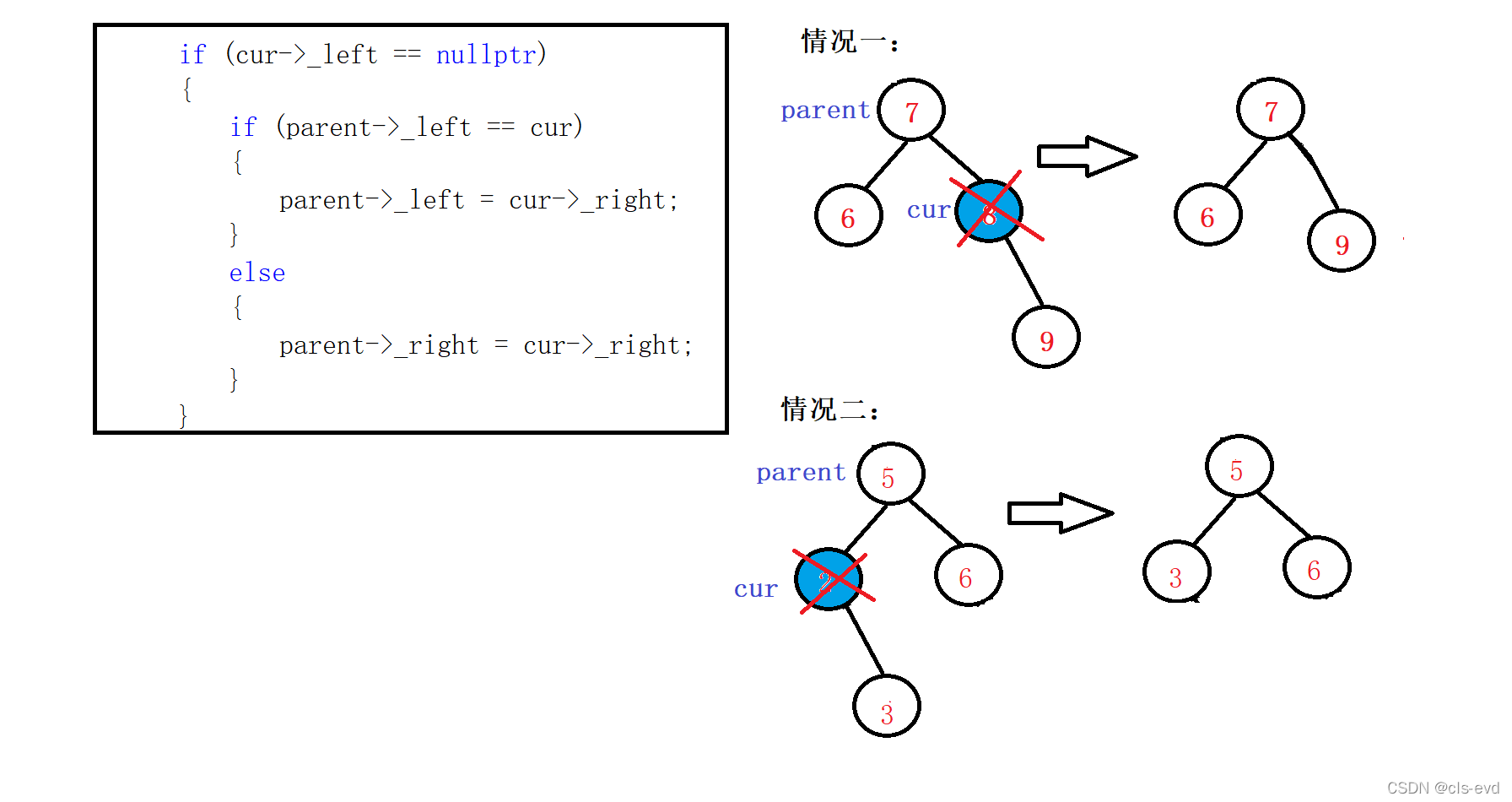
??cur的右为空的两种情况: ?cur左为空,且cur是_root.
?cur左为空,且cur是_root.
 ??cur右为空,且cur是_root.
??cur右为空,且cur是_root.
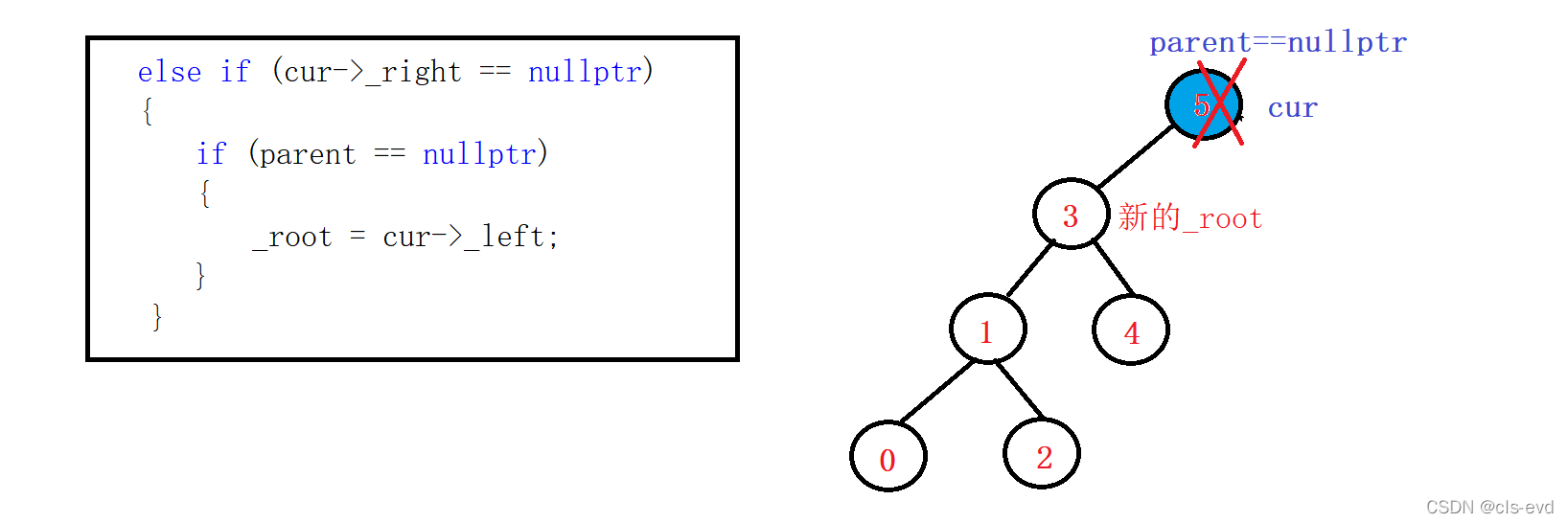
删除有两个孩子的节点:
替换节点:右子树的最左节点,这个节点的左孩子一定是空(他自己就是最左了),右孩子可能是空可能非空。
首先找到替换节点。
删除5:实例?
 ? ? ? ??
? ? ? ??
删除7:实例 ?测试结果:
?测试结果:

Find的递归写法
bool FindR(const K& key)
{
return _FindR(_root, key);
}
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
{
return nullptr;
}
if (key > root->_key)
{
_FindR(root->_right, key);
}
else if (key < root->_left)
{
_FindR(root->_left, key);
}
else
{
return root;
}
}Insert的递归写法
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (key > root->_key) //比他大递归到左边插入
{
return _InsertR(root->_right, key);
}
else if (key < root->_key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}这里的引用非常的巧妙,如果直接是传值,那么该递归就失效了。?

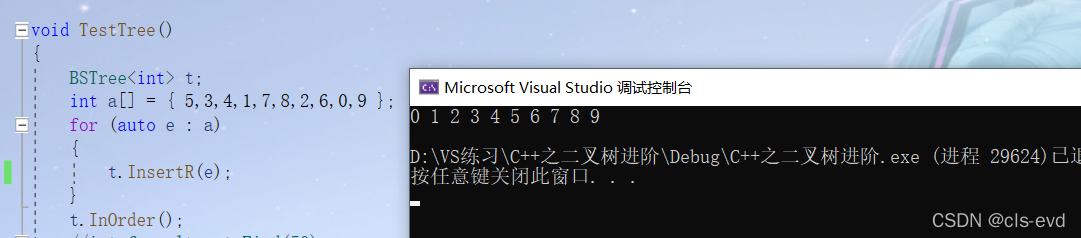
但是Insert是不推荐递归的,如果按照有序的方式插入栈就可能会爆炸!
测试:
Erase的递归实现
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (key > root->_key)
{
return _EraseR(root->_right, key);
}
else if (key < root->_key)
{
return _EraseR(root->_left, key);
}
else
{
//开始删除
Node* del = root;
if (root->_left == nullptr) //该节点的左为空
{
root = root->_right;
}
else if (root->_right == nullptr)//该节点有为空
{
root = root->_left;
}
else //节点左右都不为空
{
//寻找替换节点
Node* min = root->_right;
while (min->_left)
{
min = min->_left;
}
swap(min->_key, root->_key);
//因为这个替换节点在右子树,递归到右子树去删除
return _EraseR(root->_right, key);
//这不能忘了return 要不然里面进去删了del以后,下一行又删除了del就崩溃了
//同一块空间释放了两次
}
delete del;
return true;
}
}eg:删除8的递归展开图及原理解释?
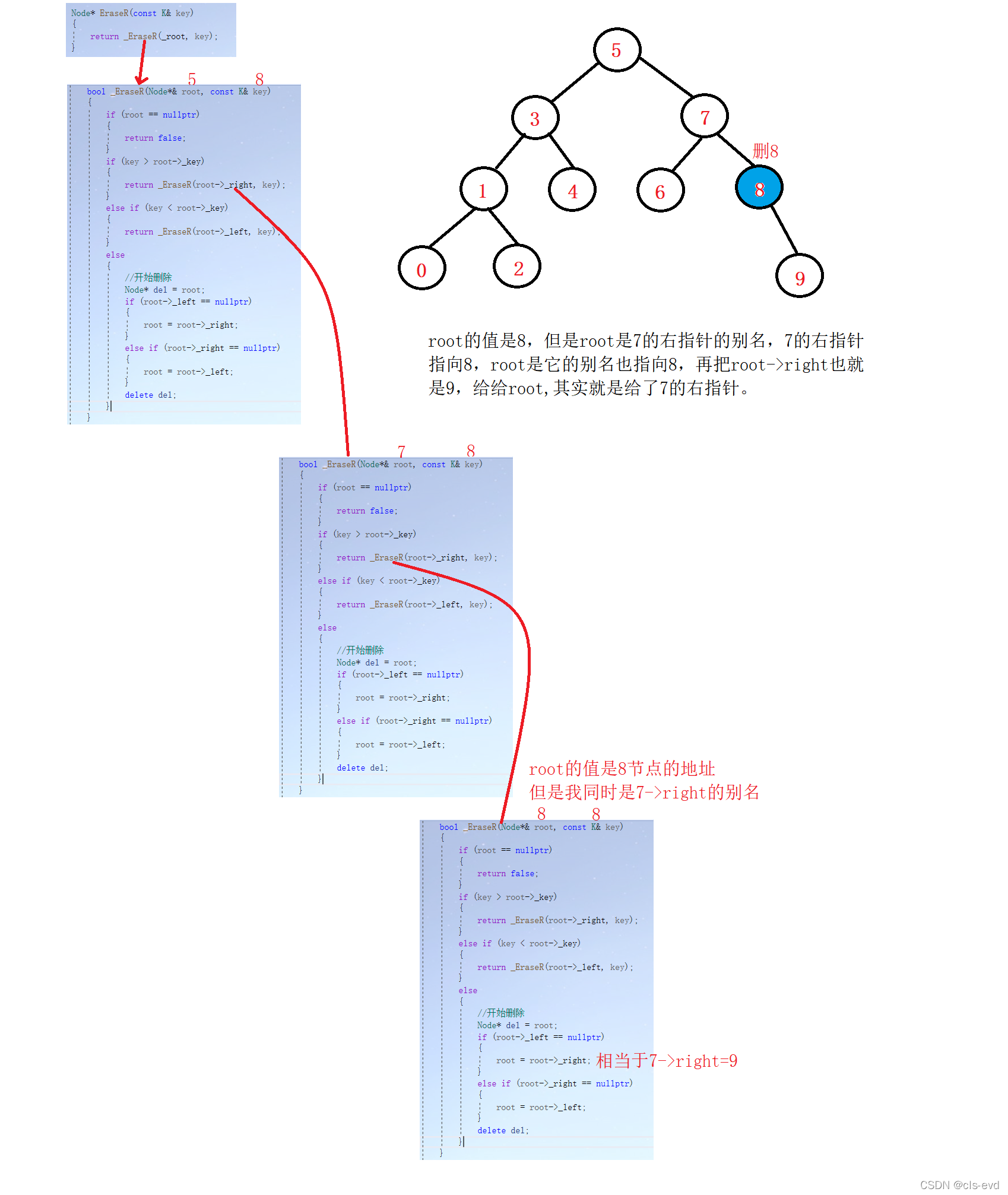
eg:删除5的递归展开图及原理展示?
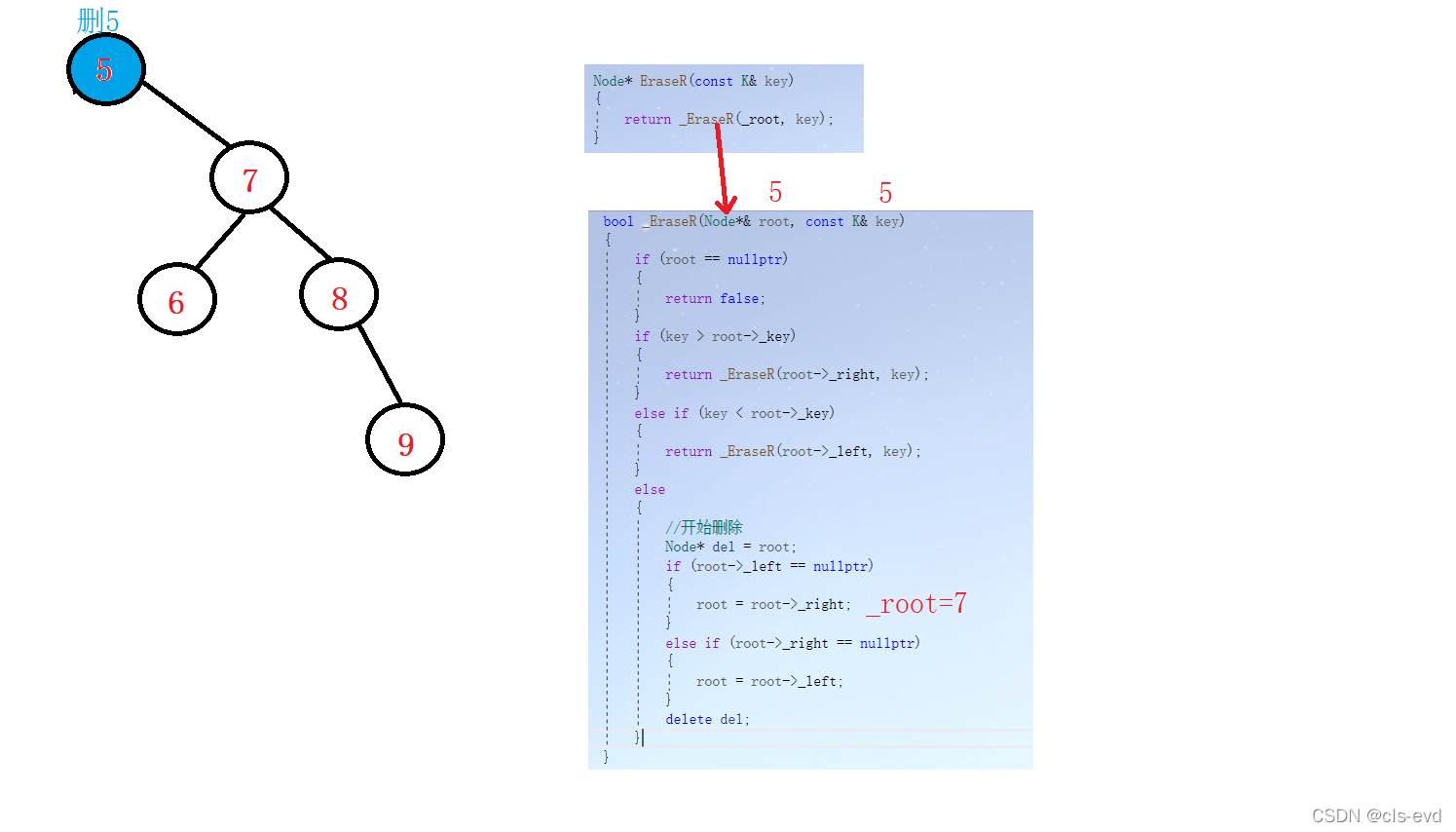
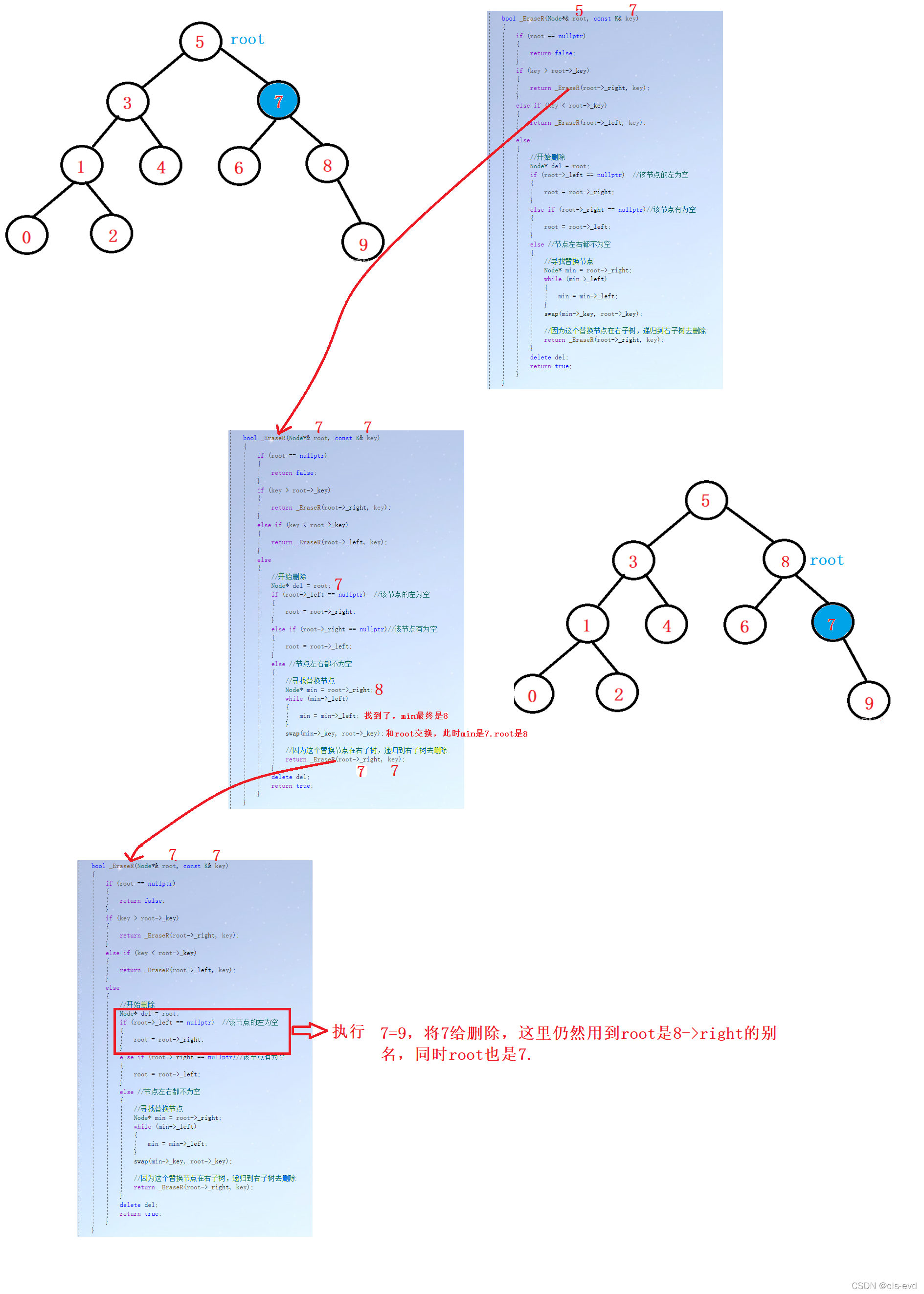
eg:删除7的递归展开图
 ?测试:
?测试:

二叉搜索树实现的完整代码:
#pragma once
#include<iostream>
using namespace std;
template<class K>
//struct BinarySearchTreeNode
struct BSTteeNode //定义结点
{
BSTteeNode<K>* _left;
BSTteeNode<K>* _right;
K _key;
BSTteeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
struct BSTree
{
typedef BSTteeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
bool Insert(const K& key)
{
//如果根为空
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr; //存储cur上一个位置
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else //数据重复返回假
{
return false;
}
}
//走到空了已经,考虑链接
cur = new Node(key);
//不知道应该链接到左边还是右边,在比较一次
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if(key<cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//找到了准备开始删除
//删除有一个孩子或者没有孩子的节点
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //删除有两个孩子的节点
{
//首先找替代节点
//替换节点:右子树的最左节点,
//这个节点的左孩子一定是空(他自己就是最左了),右孩子可能是空可能非空。
Node* minparent = cur;
Node* min = cur->_right;
while (min->_left)
{
minparent = min;
min = min->_left;
}
//找到之后覆盖要删除的节点。
cur->_key = min->_key;
//再将min删除
if (minparent->_left == min)
{
//因为是右子树的最左节点,所以一定是min的右孩子
minparent->_left = min->_right;
}
else
{
minparent->_right = min->_right;
}
delete min;
}
return true;
}
}
return false;
}
//Insert的递归版本
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (key > root->_key) //比他大递归到左边插入
{
return _InsertR(root->_right, key);
}
else if (key < root->_key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
//Find的递归版本
bool FindR(const K& key)
{
return _FindR(_root, key);
}
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
{
return nullptr;
}
if (key > root->_key)
{
_FindR(root->_right, key);
}
else if (key < root->_left)
{
_FindR(root->_left, key);
}
else
{
return root;
}
}
//Erase的递归版本
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (key > root->_key)
{
return _EraseR(root->_right, key);
}
else if (key < root->_key)
{
return _EraseR(root->_left, key);
}
else
{
//开始删除
Node* del = root;
if (root->_left == nullptr) //该节点的左为空
{
root = root->_right;
}
else if (root->_right == nullptr)//该节点有为空
{
root = root->_left;
}
else //节点左右都不为空
{
//寻找替换节点
Node* min = root->_right;
while (min->_left)
{
min = min->_left;
}
swap(min->_key, root->_key);
//因为这个替换节点在右子树,递归到右子树去删除
return _EraseR(root->_right, key);
//这不能忘了return 要不然里面进去删了del以后,下一行又删除了del就崩溃了
//同一块空间释放了两次
}
delete del;
return true;
}
}
private:
Node* _root;
};二叉搜索树的应用
- 以单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
代码实现:
template<class K, class V>
//struct BinarySearchTreeNode
struct BSTteeNode //定义结点
{
BSTteeNode<K,V>* _left;
BSTteeNode<K,V>* _right;
K _key;
V _value;
BSTteeNode(const K& key, const V& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
//key可能是身份证号
//value可能是身份信息 多张票用vector<info> _vinfo
template<class K, class V>
struct BSTree
{
typedef BSTteeNode<K, V> Node;
public:
BSTree()
:_root(nullptr)
{}
bool Insert(const K& key, const V& value)
{
//如果根为空
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node* parent = nullptr; //存储cur上一个位置
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else //数据重复返回假
{
return false;
}
}
//走到空了已经,考虑链接
cur = new Node(key,value);
//不知道应该链接到左边还是右边,在比较一次
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//找到了准备开始删除
//删除有一个孩子或者没有孩子的节点
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //删除有两个孩子的节点
{
//首先找替代节点
//替换节点:右子树的最左节点,
//这个节点的左孩子一定是空(他自己就是最左了),右孩子可能是空可能非空。
Node* minparent = cur;
Node* min = cur->_right;
while (min->_left)
{
minparent = min;
min = min->_left;
}
//找到之后覆盖要删除的节点。
cur->_key = min->_key;
cur->_value = min->_value;
//再将min删除
if (minparent->_left == min)
{
//因为是右子树的最左节点,所以一定是min的右孩子
minparent->_left = min->_right;
}
else
{
minparent->_right = min->_right;
}
delete min;
}
return true;
}
}
return false;
}
private:
Node* _root;
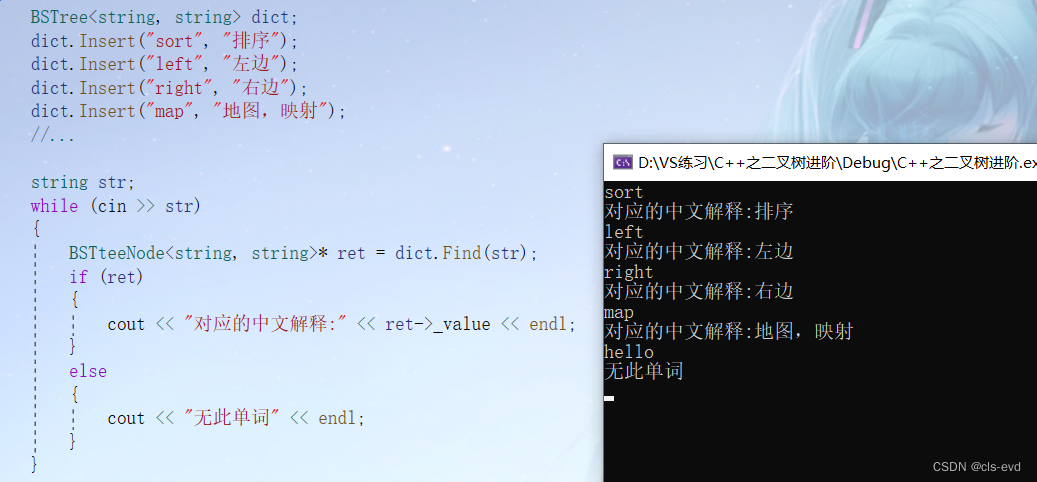
};应用1:简易版字典的实现
void TestBSTree1()
{
BSTree<string, string> dict;
dict.Insert("sort", "排序");
dict.Insert("left", "左边");
dict.Insert("right", "右边");
dict.Insert("map", "地图,映射");
//...
string str;
while (cin >> str)
{
BSTteeNode<string, string>* ret = dict.Find(str);
if (ret)
{
cout << "对应的中文解释:" << ret->_value << endl;
}
else
{
cout << "无此单词" << endl;
}
}
}
?应用2:统计水果出现的次数
void Test2()
{
//统计水果出现的次数
string arr[] = { "苹果","西瓜","苹果","西瓜","苹果","苹果","西瓜","苹果","香蕉","苹果","香蕉","草莓"};
//key是水果名称,value是出现的次数
BSTree<string, int> countTree;
for (auto& str: arr)
{
BSTteeNode<string, int>* ret = countTree.Find(str);
if (ret != nullptr)
{
ret->_value++;
}
else
{
countTree.Insert(str, 1);
}
}
countTree.InOrder();
}
?
