1.链接
http://t.csdn.cn/ezulx//平衡二叉树
AVL树的介绍网上有很多,这里就不作介绍了,这只说AVL的实现,看了80%的文章都在介绍和说明AVL树,似乎介绍实现的很少,所以尝试写写自己的见解,当然还是借鉴了上面那篇文章的实现。当然也有很多自己不好理解的实现代码,但是在看的过程中,自己慢慢体会到了其中的奥妙,能够明白怎么实现了,就自己写实现代码了。
2.AVL的树调整
AVL的调整主要包括对某棵子树(或整棵树)的左旋和右旋。这两个操作,是针对某两个点执行的,对左倾的右旋,对右倾的左旋。
代码的实现方式按照自己的需求写。
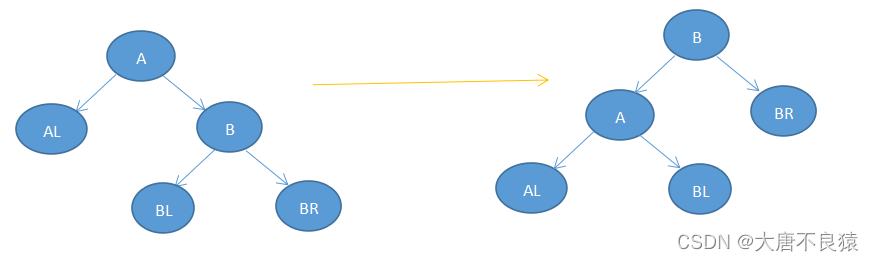
2.1.左旋
左旋的是A结点,leftRotate(A)函数返回的结点结果如右图。
_AVLTreeNodePtr leftRotate(_AVLTreeNodePtr node)
{
_AVLTreeNodePtr nodeRight = node->m_rightChild;
node->m_rightChild = nodeRight->m_leftChild;
nodeRight->m_leftChild = node;
return nodeRight;
}
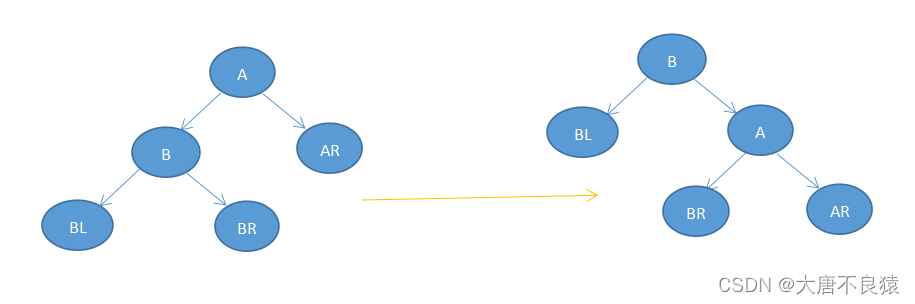
2.2.右旋
右旋的是A结点,rightRotate(A)函数返回的结点结果如右图。
_AVLTreeNodePtr rightRotate(_AVLTreeNodePtr node)
{
_AVLTreeNodePtr nodeLeft = node->m_leftChild;
node->m_leftChild = nodeLeft->m_rightChild;
nodeLeft->m_rightChild = node;
return nodeLeft;
}
3.实现
3.1.结点定义
添加构造函数方便于构造结点。
template <typename _dataType>
struct AVLTreeNode
{
_dataType m_value;
AVLTreeNode* m_leftChild;
AVLTreeNode* m_rightChild;
AVLTreeNode() : m_value(_dataType()), m_leftChild(nullptr), m_rightChild(nullptr) {}
AVLTreeNode(_dataType value, AVLTreeNode* leftChild = nullptr, AVLTreeNode* rightChild = nullptr)
: m_value(value), m_leftChild(leftChild), m_rightChild(rightChild) {}
};
3.2.插入和删除
我看了很多博文,也看了许多的时评,找到了两种实现方法,我第一种能想到的就是先插入/删除再调整,然后在上面的链接中,看到了在插入/删除的过程中调整的方案。
3.2.1.先插入/删除后调整
因为是封装的树,所以提供给外部的插入/删除接口如下,插入和删除的接口中都是先进行插入/删除,再进行调整。
//插入
bool insert(_dataType value)
{
insert(m_root, value);
adjustment(m_root);
return true;
}
//删除
bool remove(_dataType value)
{
remove(m_root, value);
adjustment(m_root);
return true;
}
3.2.1.1.插入数据
这里的设计支持添加重复数据。大于等于根节点的添加在右边,否则添加在左边。
//插入
bool insert(_AVLTreeNodePtr& root, _dataType value)
{
if (root)
{
return (value >= root->m_value) ? insert(root->m_rightChild, value) : insert(root->m_leftChild, value);
}
else
{
root = new AVLTreeNode<_dataType>(value);
return true;
}
}
3.2.1.2.删除数据
支持删除重复数据。
//删除
bool remove(_AVLTreeNodePtr& root, _dataType value)
{
if (root)
{
if (value == root->m_value)
{
if (root->m_rightChild)
{
if (root->m_rightChild->m_leftChild)
{
_AVLTreeNodePtr RMNodeParent = root->m_rightChild;
while (RMNodeParent->m_leftChild->m_leftChild)
{
RMNodeParent = RMNodeParent->m_leftChild;
}
std::swap(root->m_value, RMNodeParent->m_leftChild->m_value);
_AVLTreeNodePtr rNode = RMNodeParent->m_leftChild;
RMNodeParent->m_leftChild = RMNodeParent->m_leftChild->m_rightChild;
delete rNode;
rNode = nullptr;
return remove(root, value);
}
else
{
_AVLTreeNodePtr rNode = root;
root->m_rightChild->m_leftChild = root->m_leftChild;
root = root->m_rightChild;
delete rNode;
rNode = nullptr;
return remove(root, value);
}
}
else
{
_AVLTreeNodePtr rNode = root;
root = root->m_leftChild;
delete rNode;
rNode = nullptr;
return true;
}
}
else if (value > root->m_value)
{
return remove(root->m_rightChild, value);
}
else
{
return remove(root->m_leftChild, value);
}
}
else
{
return false;
}
}
3.2.1.3.判断某个结点是否需要调整
左右孩子高度差大于1就需要调整。
bool needAdjustment(_AVLTreeNodePtr root)
{
if(root == nullptr)
{
return false;
}
size_t leftHeight = height(root->m_leftChild);
size_t rightHeight = height(root->m_rightChild);
if(leftHeight > rightHeight)
{
return leftHeight - rightHeight > 1;
}
else
{
return rightHeight - leftHeight > 1;
}
}
3.2.1.4.查找某个结点是否需要调整
直接看注释。
bool adjustment(_AVLTreeNodePtr& root)
{
if (root)//如果该节点不为空
{
if (needAdjustment(root))//该节点需要调整
{
if (needAdjustment(root->m_leftChild))//如果该节点的左孩子需要调整
{
return adjustment(root->m_leftChild);//调整左孩子
}
else if (needAdjustment(root->m_rightChild))//如果该节点的右孩子需要调整
{
return adjustment(root->m_rightChild);//调整右孩子
}
else
{
bool l = adjustment(root->m_leftChild);//查找左孩子树是否需要调整
bool r = adjustment(root->m_rightChild);//查找右孩子树是否需要调整
return l || r ? true : adjustmentNode(root);//如果左孩子树或者右孩子树已经有调整,则直接返回true,否则调整该结点
}
}
else//该结点不需要调整
{
bool l = adjustment(root->m_leftChild);//查找左孩子树是否需要调整
bool r = adjustment(root->m_rightChild);//查找右孩子树是否需要调整
return l || r;
}
}
else
{
return false;
}
}
3.2.1.5.调整结点
通过比较左右孩子的高度来判断属于哪个类型。左旋和右旋函数在上面
bool adjustmentNode(_AVLTreeNodePtr& root)
{
if (height(root->m_leftChild) > height(root->m_rightChild))
{
if (height(root->m_leftChild->m_leftChild) > height(root->m_leftChild->m_rightChild))//LL
{
root = rightRotate(root);
}
else//LR
{
root->m_leftChild = leftRotate(root->m_leftChild);
root = rightRotate(root);
}
}
else
{
if (height(root->m_rightChild->m_rightChild) > height(root->m_rightChild->m_leftChild))//RR
{
root = leftRotate(root);
}
else//RL
{
root->m_rightChild = rightRotate(root->m_rightChild);
root = leftRotate(root);
}
}
return true;
}
3.2.1.6.实现代码
#pragma once
#ifndef AVLTREENODE_H
#define AVLTREENODE_H
#include <iostream>
template <typename _dataType>
struct AVLTreeNode
{
_dataType m_value;
AVLTreeNode* m_leftChild;
AVLTreeNode* m_rightChild;
AVLTreeNode() : m_value(_dataType()), m_leftChild(nullptr), m_rightChild(nullptr) {}
AVLTreeNode(_dataType value, AVLTreeNode* leftChild = nullptr, AVLTreeNode* rightChild = nullptr)
: m_value(value), m_leftChild(leftChild), m_rightChild(rightChild) {}
};
template <typename _dataType>
class AVLTree
{
using _AVLTreeNodePtr = AVLTreeNode<_dataType>*;
public:
AVLTree()
: m_root(nullptr)
{
}
AVLTree(const AVLTree& avlt)
{
copy(m_root, avlt.m_root);
}
~AVLTree()
{
clear(m_root);
}
AVLTree& operator = (const AVLTree& avlt)
{
clear(m_root);
copy(m_root, avlt.m_root);
return *this;
}
//节点数
size_t size()
{
return size(m_root);
}
//高度
size_t height()
{
return height(m_root);
}
//叶子树
size_t leafCount()
{
return leafCount(m_root);
}
//插入
bool insert(_dataType value)
{
insert(m_root, value);
adjustment(m_root);
return true;
}
//删除
bool remove(_dataType value)
{
remove(m_root, value);
adjustment(m_root);
return true;
}
//先序遍历
void preorderTraverse()
{
preorderTraverse(m_root);
}
//中序遍历
void midorderTraverse()
{
midorderTraverse(m_root);
}
//后序遍历
void postorderTraverse()
{
postorderTraverse(m_root);
}
//清楚
void clear()
{
clear(m_root);
}
bool hasHeightSubMax2()
{
return hasHeightSubMax2(m_root);
}
protected:
void preorderTraverse(_AVLTreeNodePtr root)
{
if (root)
{
std::cout << root->m_value << ", ";
preorderTraverse(root->m_leftChild);
preorderTraverse(root->m_rightChild);
}
}
void midorderTraverse(_AVLTreeNodePtr root)
{
if (root)
{
midorderTraverse(root->m_leftChild);
std::cout << root->m_value << ", ";
midorderTraverse(root->m_rightChild);
}
}
void postorderTraverse(_AVLTreeNodePtr root)
{
if (root)
{
postorderTraverse(root->m_leftChild);
postorderTraverse(root->m_rightChild);
std::cout << root->m_value << ", ";
}
}
bool hasHeightSubMax2(_AVLTreeNodePtr root)
{
if (root)
{
if (needAdjustment(root))
{
return true;
}
else
{
return hasHeightSubMax2(root->m_leftChild) || hasHeightSubMax2(root->m_rightChild);
}
}
else
{
return false;
}
}
//节点数
size_t size(_AVLTreeNodePtr root)
{
return (root) ? size(root->m_leftChild) + size(root->m_rightChild) + 1 : 0;
}
//高度
size_t height(_AVLTreeNodePtr root)
{
return (root) ? std::max(height(root->m_leftChild), height(root->m_rightChild)) + 1 : 0;
}
//叶子数
size_t leafCount(_AVLTreeNodePtr root)
{
if (root)
{
if (root->m_leftChild && root->m_rightChild)
{
return leafCount(root->m_leftChild) + leafCount(root->m_rightChild);
}
else if (root->m_leftChild)
{
return leafCount(root->m_leftChild);
}
else if (root->m_rightChild)
{
return leafCount(root->m_rightChild);
}
else
{
return 1;
}
}
else
{
return 0;
}
}
bool needAdjustment(_AVLTreeNodePtr root)
{
if (root == nullptr)
{
return false;
}
size_t leftHeight = height(root->m_leftChild);
size_t rightHeight = height(root->m_rightChild);
if (leftHeight > rightHeight)
{
return leftHeight - rightHeight > 1;
}
else
{
return rightHeight - leftHeight > 1;
}
}
bool adjustment(_AVLTreeNodePtr& root)
{
if (root)
{
if (needAdjustment(root))
{
if (needAdjustment(root->m_leftChild))
{
return adjustment(root->m_leftChild);
}
else if (needAdjustment(root->m_rightChild))
{
return adjustment(root->m_rightChild);
}
else
{
bool l = adjustment(root->m_leftChild);
bool r = adjustment(root->m_rightChild);
return l || r ? true : adjustmentNode(root);
}
}
else
{
bool l = adjustment(root->m_leftChild);
bool r = adjustment(root->m_rightChild);
return l || r;
}
}
else
{
return false;
}
}
_AVLTreeNodePtr leftRotate(_AVLTreeNodePtr node)
{
_AVLTreeNodePtr nodeRight = node->m_rightChild;
node->m_rightChild = nodeRight->m_leftChild;
nodeRight->m_leftChild = node;
return nodeRight;
}
_AVLTreeNodePtr rightRotate(_AVLTreeNodePtr node)
{
_AVLTreeNodePtr nodeLeft = node->m_leftChild;
node->m_leftChild = nodeLeft->m_rightChild;
nodeLeft->m_rightChild = node;
return nodeLeft;
}
bool adjustmentNode(_AVLTreeNodePtr& root)
{
if (height(root->m_leftChild) > height(root->m_rightChild))
{
if (height(root->m_leftChild->m_leftChild) > height(root->m_leftChild->m_rightChild))//LL
{
root = rightRotate(root);
}
else//LR
{
root->m_leftChild = leftRotate(root->m_leftChild);
root = rightRotate(root);
}
}
else
{
if (height(root->m_rightChild->m_rightChild) > height(root->m_rightChild->m_leftChild))//RR
{
root = leftRotate(root);
}
else//RL
{
root->m_rightChild = rightRotate(root->m_rightChild);
root = leftRotate(root);
}
}
return true;
}
//插入
bool insert(_AVLTreeNodePtr& root, _dataType value)
{
if (root)
{
return (value >= root->m_value) ? insert(root->m_rightChild, value) : insert(root->m_leftChild, value);
}
else
{
root = new AVLTreeNode<_dataType>(value);
return true;
}
}
//删除
bool remove(_AVLTreeNodePtr& root, _dataType value)
{
if (root)
{
if (value == root->m_value)
{
if (root->m_rightChild)
{
if (root->m_rightChild->m_leftChild)
{
_AVLTreeNodePtr RMNodeParent = root->m_rightChild;
while (RMNodeParent->m_leftChild->m_leftChild)
{
RMNodeParent = RMNodeParent->m_leftChild;
}
std::swap(root->m_value, RMNodeParent->m_leftChild->m_value);
_AVLTreeNodePtr rNode = RMNodeParent->m_leftChild;
RMNodeParent->m_leftChild = RMNodeParent->m_leftChild->m_rightChild;
delete rNode;
rNode = nullptr;
return remove(root, value);
}
else
{
_AVLTreeNodePtr rNode = root;
root->m_rightChild->m_leftChild = root->m_leftChild;
root = root->m_rightChild;
delete rNode;
rNode = nullptr;
return remove(root, value);
}
}
else
{
_AVLTreeNodePtr rNode = root;
root = root->m_leftChild;
delete rNode;
rNode = nullptr;
return true;
}
}
else if (value > root->m_value)
{
return remove(root->m_rightChild, value);
}
else
{
return remove(root->m_leftChild, value);
}
}
else
{
return false;
}
}
//清除
void clear(_AVLTreeNodePtr root)
{
if (root)
{
clear(root->m_leftChild);
clear(root->m_rightChild);
delete root;
root = nullptr;
}
}
void copy(_AVLTreeNodePtr& root1, _AVLTreeNodePtr root2)
{
if (root2)
{
root1 = new AVLTreeNode<_dataType>(root2->m_value);
copy(root1->m_leftChild, root2->m_leftChild);
copy(root1->m_rightChild, root2->m_rightChild);
}
}
private:
_AVLTreeNodePtr m_root;
};
#endif // AVLTREENODE_H
3.2.1.7.测试代码
#include <iostream>
#include "avl2.h"
int main()
{
AVLTree<int> rbt;
for (int num = 1; num <= 10000; num++)
{
rbt.insert(num);
}
std::cout << "\n中序遍历:";
rbt.midorderTraverse();
std::cout << "height = " << rbt.height() << std::endl;
std::cout << "----------------------------" << std::endl;
for (int num = 10; num <= 2000; num++)
{
rbt.remove(num);
}
std::cout << "\n中序遍历:";
rbt.midorderTraverse();
std::cout << "height = " << rbt.height() << std::endl;
return 0;
}
3.2.1.8.测试结果
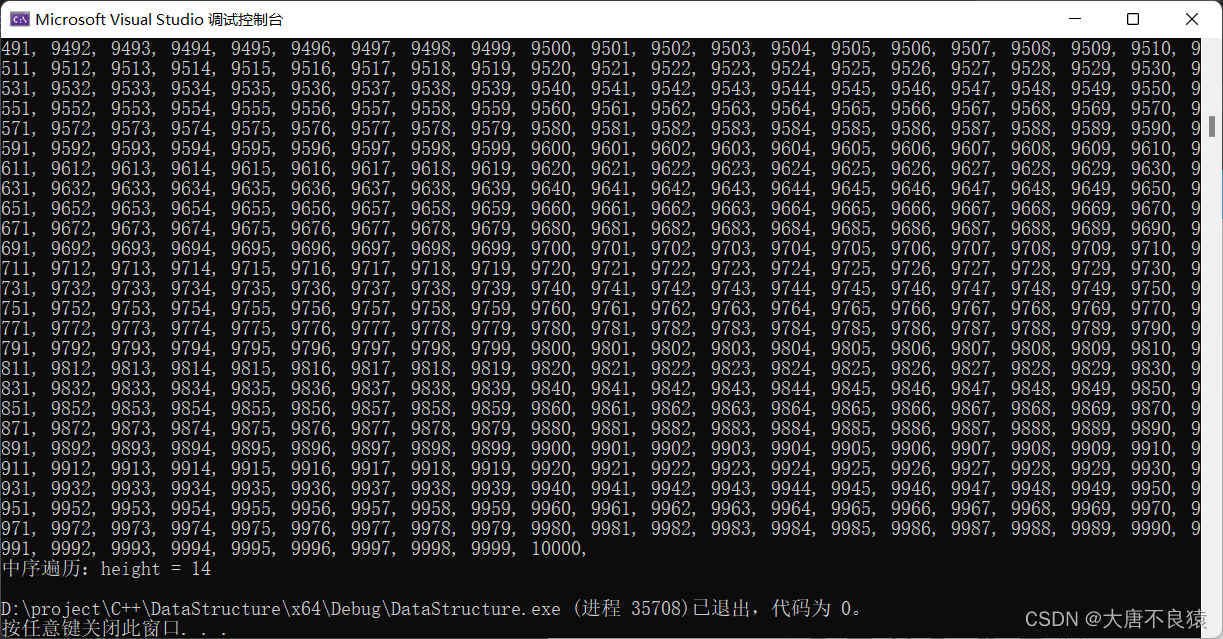
3.2.1.9.总结
有一种实现方式是记录每个结点的高度,(上面链接中的实现方式),不记录的话每次都要求高度,提高了时间复杂度,我写的这个如果结点数十万的话,就很久很久才能走完了。
3.2.2.在插入/删除过程中调整
这种实现方式,我们就添加结点高度这么一个属性,这样提高了运行速度:
//AVL树的结点
template <typename _dataType>
struct AVLTreeNode
{
_dataType m_value; //结点存储的数据,必须可比较
size_t m_height; //该结点在树中的高度,默认高度是1
AVLTreeNode* m_leftChild; //该结点的左孩子
AVLTreeNode* m_rightChild; //该结点的有孩子
AVLTreeNode() : m_value(_dataType()), m_height(1), m_leftChild(nullptr), m_rightChild(nullptr) {}
AVLTreeNode(_dataType value, AVLTreeNode* leftChild = nullptr, AVLTreeNode* rightChild = nullptr)
: m_value(value), m_height(1), m_leftChild(leftChild), m_rightChild(rightChild) {}
};
提供给外部插入/删除接口为:
//插入
void insert(_dataType value)
{
m_root = insert(m_root, value);
}
//删除
void remove(_dataType value)
{
m_root = remove(m_root, value);
}
3.2.2.1.插入
插入之后,调整高度,判断是否需要调整,这就从底向上检查,调整的是最接近新插入的结点的结点,只需调整一次就行。
//插入一个新的数据,支持插入重复数据
_AVLTreeNodePtr insert(_AVLTreeNodePtr root, _dataType value)
{
if (root == nullptr)
{
return new AVLTreeNode<_dataType>(value);
}
else
{
if (value >= root->m_value)
{
root->m_rightChild = insert(root->m_rightChild, value);
}
else
{
root->m_leftChild = insert(root->m_leftChild, value);
}
}
root->m_height = std::max(heightval(root->m_leftChild), heightval(root->m_rightChild)) + 1;
return needAdjustment(root) ? adjust(root) : root;
} //end insert
3.2.2.2.删除
删除的步骤差不多。
//删除一个已有数据,支持删除重复的多个数据
_AVLTreeNodePtr remove(_AVLTreeNodePtr root, _dataType value)
{
if (root == nullptr)
{
return root;
}
else
{
if (value > root->m_value)
{
root->m_rightChild = remove(root->m_rightChild, value);
}
else if(value < root->m_value)
{
root->m_leftChild = remove(root->m_leftChild, value);
}
else
{
if (root->m_leftChild == nullptr || root->m_rightChild == nullptr)
{
_AVLTreeNodePtr node = root;
root = (root->m_leftChild == nullptr) ? root->m_rightChild : root->m_leftChild;
delete node;
node = nullptr;
}
else
{
if (root->m_rightChild->m_leftChild)
{
_AVLTreeNodePtr RMNodeParent = root->m_rightChild;
while (RMNodeParent->m_leftChild->m_leftChild)
{
RMNodeParent = RMNodeParent->m_leftChild;
}
root->m_value = RMNodeParent->m_leftChild->m_value;
_AVLTreeNodePtr rNode = RMNodeParent->m_leftChild;
RMNodeParent->m_leftChild = RMNodeParent->m_leftChild->m_rightChild;
delete rNode;
rNode = nullptr;
}
else
{
_AVLTreeNodePtr rNode = root;
root->m_rightChild->m_leftChild = root->m_leftChild;
root = root->m_rightChild;
delete rNode;
rNode = nullptr;
}
}
root = remove(root, value);
}
if (!root)
{
return nullptr;
}
else
{
root->m_height = std::max(heightval(root->m_leftChild), heightval(root->m_rightChild)) + 1;
return needAdjustment(root) ? adjust(root) : root;
}
}
} //end remove
3.2.2.3.获取结点高度
size_t heightval(_AVLTreeNodePtr root)
{
return (root) ? root->m_height : 0;
}
3.2.2.4.判断是否需要调整
bool needAdjustment(_AVLTreeNodePtr root)
{
return llabs(heightval(root->m_leftChild) - heightval(root->m_rightChild)) > 1;
}
3.2.2.5.左旋
旋转之后要调整高度。
_AVLTreeNodePtr leftRotate(_AVLTreeNodePtr node)
{
_AVLTreeNodePtr nodeRight = node->m_rightChild;
node->m_rightChild = nodeRight->m_leftChild;
nodeRight->m_leftChild = node;
node->m_height = std::max(heightval(node->m_leftChild), heightval(node->m_rightChild)) + 1;
nodeRight->m_height = std::max(heightval(nodeRight->m_leftChild), heightval(nodeRight->m_rightChild)) + 1;
return nodeRight;
} //end leftRotate
3.2.2.6.右旋
旋转之后要调整高度。
_AVLTreeNodePtr rightRotate(_AVLTreeNodePtr node)
{
_AVLTreeNodePtr nodeLeft = node->m_leftChild;
node->m_leftChild = nodeLeft->m_rightChild;
nodeLeft->m_rightChild = node;
node->m_height = std::max(heightval(node->m_leftChild), heightval(node->m_rightChild)) + 1;
nodeLeft->m_height = std::max(heightval(nodeLeft->m_leftChild), heightval(nodeLeft->m_rightChild)) + 1;
return nodeLeft;
} //end rightRotate
3.2.2.7.调整
调整代码是一样的。
_AVLTreeNodePtr adjust(_AVLTreeNodePtr root)
{
if (heightval(root->m_leftChild) > heightval(root->m_rightChild))
{
if (heightval(root->m_leftChild->m_leftChild) > heightval(root->m_leftChild->m_rightChild))//LL
{
root = rightRotate(root);
}
else//LR
{
root->m_leftChild = leftRotate(root->m_leftChild);
root = rightRotate(root);
}
}
else
{
if (heightval(root->m_rightChild->m_rightChild) > heightval(root->m_rightChild->m_leftChild))//RR
{
root = leftRotate(root);
}
else//RL
{
root->m_rightChild = rightRotate(root->m_rightChild);
root = leftRotate(root);
}
}
return root;
} //end adjust
3.2.2.8.实现代码
不多。
#pragma once
#ifndef _AVLTREE_H_
#define _AVLTREE_H_
#include <iostream>
#include <stack>
#include <queue>
#include <unordered_map>
//AVL树的结点
template <typename _dataType>
struct AVLTreeNode
{
_dataType m_value; //结点存储的数据,必须可比较
size_t m_height; //该结点在树中的高度,默认高度是1
AVLTreeNode* m_leftChild; //该结点的左孩子
AVLTreeNode* m_rightChild; //该结点的有孩子
AVLTreeNode() : m_value(_dataType()), m_height(1), m_leftChild(nullptr), m_rightChild(nullptr) {}
AVLTreeNode(_dataType value, AVLTreeNode* leftChild = nullptr, AVLTreeNode* rightChild = nullptr)
: m_value(value), m_height(1), m_leftChild(leftChild), m_rightChild(rightChild) {}
};
template <typename _dataType>
class AVLTree
{
using _AVLTreeNodePtr = AVLTreeNode<_dataType>*;
public:
AVLTree()
: m_root(nullptr)
{
}
AVLTree(const AVLTree& avlt)
{
copy(m_root, avlt.m_root);
}
~AVLTree()
{
clear(m_root);
}
AVLTree& operator = (const AVLTree& avlt)
{
clear(m_root);
copy(m_root, avlt.m_root);
return *this;
}
//节点数
size_t size()
{
return size(m_root);
}
//高度
size_t height()
{
return heightval(m_root);
}
//叶子树
size_t leafCount()
{
return leafCount(m_root);
}
//插入
void insert(_dataType value)
{
m_root = insert(m_root, value);
}
//删除
void remove(_dataType value)
{
m_root = remove(m_root, value);
}
//先序遍历
void preorderTraverse()
{
preorderTraverse(m_root);
}
//中序遍历
void midorderTraverse()
{
midorderTraverse(m_root);
}
//后序遍历
void postorderTraverse()
{
postorderTraverse(m_root);
}
void levelTraversal()
{
std::unordered_map< _AVLTreeNodePtr, int> treemap;
std::queue<_AVLTreeNodePtr> treeNodeStack;
_AVLTreeNodePtr root = m_root;
std::vector<std::vector<int>> nums;
treeNodeStack.push(root);
treemap[root] = 1;
while (!treeNodeStack.empty()) {
root = treeNodeStack.front();
treeNodeStack.pop();
if (treemap[root] > nums.size())
{
nums.push_back(std::vector<int>(1, root->m_value));
}
else
{
nums[treemap[root] - 1].push_back(root->m_value);
}
if (root->m_leftChild) {
treeNodeStack.push(root->m_leftChild);
treemap[root->m_leftChild] = treemap[root] + 1;
}
if (root->m_rightChild) {
treeNodeStack.push(root->m_rightChild);
treemap[root->m_rightChild] = treemap[root] + 1;
}
}
std::cout << std::endl;
for (int i = 0; i < nums.size(); i++)
{
for (int j = 0; j < nums[i].size(); j++)
{
std::cout << nums[i][j] << ", ";
}
std::cout << std::endl;
}
}
//清除
void clear()
{
clear(m_root);
}
bool hasHeightSubMax2()
{
return m_root ? hasHeightSubMax2(m_root->m_leftChild, m_root->m_rightChild) : true;
}
protected:
bool hasHeightSubMax2(_AVLTreeNodePtr left, _AVLTreeNodePtr right)
{
if (left || right)
{
if (llabs(height(left) - height(right)) > 1)
{
return true;
}
else
{
if (left && right)
{
return hasHeightSubMax2(left->m_leftChild, left->m_rightChild)
|| hasHeightSubMax2(right->m_leftChild, right->m_rightChild);
}
else if (left)
{
return hasHeightSubMax2(left->m_leftChild, left->m_rightChild);
}
else
{
return hasHeightSubMax2(right->m_leftChild, right->m_rightChild);
}
}
}
else
{
return false;
}
}
//节点数
size_t size(_AVLTreeNodePtr root)
{
return (root) ? size(root->m_leftChild) + size(root->m_rightChild) + 1 : 0;
}
//高度
size_t height(_AVLTreeNodePtr root)
{
return (root) ? std::max(height(root->m_leftChild), height(root->m_rightChild)) + 1 : 0;
}
//叶子数
size_t leafCount(_AVLTreeNodePtr root)
{
if (root)
{
if (root->m_leftChild && root->m_rightChild)
{
return leafCount(root->m_leftChild) + leafCount(root->m_rightChild);
}
else if (root->m_leftChild)
{
return leafCount(root->m_leftChild);
}
else if (root->m_rightChild)
{
return leafCount(root->m_rightChild);
}
else
{
return 1;
}
}
else
{
return 0;
}
}
size_t heightval(_AVLTreeNodePtr root)
{
return (root) ? root->m_height : 0;
}
bool needAdjustment(_AVLTreeNodePtr root)
{
return llabs(heightval(root->m_leftChild) - heightval(root->m_rightChild)) > 1;
}
_AVLTreeNodePtr leftRotate(_AVLTreeNodePtr node)
{
_AVLTreeNodePtr nodeRight = node->m_rightChild;
node->m_rightChild = nodeRight->m_leftChild;
nodeRight->m_leftChild = node;
node->m_height = std::max(heightval(node->m_leftChild), heightval(node->m_rightChild)) + 1;
nodeRight->m_height = std::max(heightval(nodeRight->m_leftChild), heightval(nodeRight->m_rightChild)) + 1;
return nodeRight;
} //end leftRotate
_AVLTreeNodePtr rightRotate(_AVLTreeNodePtr node)
{
_AVLTreeNodePtr nodeLeft = node->m_leftChild;
node->m_leftChild = nodeLeft->m_rightChild;
nodeLeft->m_rightChild = node;
node->m_height = std::max(heightval(node->m_leftChild), heightval(node->m_rightChild)) + 1;
nodeLeft->m_height = std::max(heightval(nodeLeft->m_leftChild), heightval(nodeLeft->m_rightChild)) + 1;
return nodeLeft;
} //end rightRotate
_AVLTreeNodePtr adjust(_AVLTreeNodePtr root)
{
if (heightval(root->m_leftChild) > heightval(root->m_rightChild))
{
if (heightval(root->m_leftChild->m_leftChild) > heightval(root->m_leftChild->m_rightChild))//LL
{
root = rightRotate(root);
}
else//LR
{
root->m_leftChild = leftRotate(root->m_leftChild);
root = rightRotate(root);
}
}
else
{
if (heightval(root->m_rightChild->m_rightChild) > heightval(root->m_rightChild->m_leftChild))//RR
{
root = leftRotate(root);
}
else//RL
{
root->m_rightChild = rightRotate(root->m_rightChild);
root = leftRotate(root);
}
}
return root;
} //end adjust
//插入一个新的数据,支持插入重复数据
_AVLTreeNodePtr insert(_AVLTreeNodePtr root, _dataType value)
{
if (root == nullptr)
{
return new AVLTreeNode<_dataType>(value);
}
else
{
if (value >= root->m_value)
{
root->m_rightChild = insert(root->m_rightChild, value);
}
else
{
root->m_leftChild = insert(root->m_leftChild, value);
}
}
root->m_height = std::max(heightval(root->m_leftChild), heightval(root->m_rightChild)) + 1;
return needAdjustment(root) ? adjust(root) : root;
} //end insert
//删除一个已有数据,支持删除重复的多个数据
_AVLTreeNodePtr remove(_AVLTreeNodePtr root, _dataType value)
{
if (root == nullptr)
{
return root;
}
else
{
if (value > root->m_value)
{
root->m_rightChild = remove(root->m_rightChild, value);
}
else if(value < root->m_value)
{
root->m_leftChild = remove(root->m_leftChild, value);
}
else
{
if (root->m_leftChild == nullptr || root->m_rightChild == nullptr)
{
_AVLTreeNodePtr node = root;
root = (root->m_leftChild == nullptr) ? root->m_rightChild : root->m_leftChild;
delete node;
node = nullptr;
}
else
{
if (root->m_rightChild->m_leftChild)
{
_AVLTreeNodePtr RMNodeParent = root->m_rightChild;
while (RMNodeParent->m_leftChild->m_leftChild)
{
RMNodeParent = RMNodeParent->m_leftChild;
}
root->m_value = RMNodeParent->m_leftChild->m_value;
_AVLTreeNodePtr rNode = RMNodeParent->m_leftChild;
RMNodeParent->m_leftChild = RMNodeParent->m_leftChild->m_rightChild;
delete rNode;
rNode = nullptr;
}
else
{
_AVLTreeNodePtr rNode = root;
root->m_rightChild->m_leftChild = root->m_leftChild;
root = root->m_rightChild;
delete rNode;
rNode = nullptr;
}
}
root = remove(root, value);
}
if (!root)
{
return nullptr;
}
else
{
root->m_height = std::max(heightval(root->m_leftChild), heightval(root->m_rightChild)) + 1;
return needAdjustment(root) ? adjust(root) : root;
}
}
} //end remove
//先序遍历
void preorderTraverse(_AVLTreeNodePtr root)
{
if (root)
{
std::cout << root->m_value << ", ";
preorderTraverse(root->m_leftChild);
preorderTraverse(root->m_rightChild);
}
}
//中序遍历
void midorderTraverse(_AVLTreeNodePtr root)
{
if (root)
{
midorderTraverse(root->m_leftChild);
std::cout << root->m_value << ", ";
midorderTraverse(root->m_rightChild);
}
}
//后序遍历
void postorderTraverse(_AVLTreeNodePtr root)
{
if (root)
{
postorderTraverse(root->m_leftChild);
postorderTraverse(root->m_rightChild);
std::cout << root->m_value << ", ";
}
}
//清除
void clear(_AVLTreeNodePtr root)
{
if (root)
{
clear(root->m_leftChild);
clear(root->m_rightChild);
delete root;
root = nullptr;
}
}
void copy(_AVLTreeNodePtr& root1, _AVLTreeNodePtr root2)
{
if (root2)
{
root1 = new AVLTreeNode<_dataType>(root2->m_value);
copy(root1->m_leftChild, root2->m_leftChild);
copy(root1->m_rightChild, root2->m_rightChild);
}
}
private:
_AVLTreeNodePtr m_root;
};
#endif // !_AVLTREE_H_
3.2.2.9.测试代码
#include <iostream>
#include "avltree.h"
int main()
{
AVLTree<int> rbt;
for (int num = 1; num <= 1000000; num++)
{
rbt.insert(num);
}
std::cout << "\n中序遍历:";
rbt.midorderTraverse();
std::cout << "height = " << rbt.height() << std::endl;
std::cout << "----------------------------" << std::endl;
for (int num = 10; num <= 2000; num++)
{
rbt.remove(num);
}
std::cout << "\n中序遍历:";
rbt.midorderTraverse();
std::cout << "height = " << rbt.height() << std::endl;
return 0;
}
3.2.2.10.输出结果
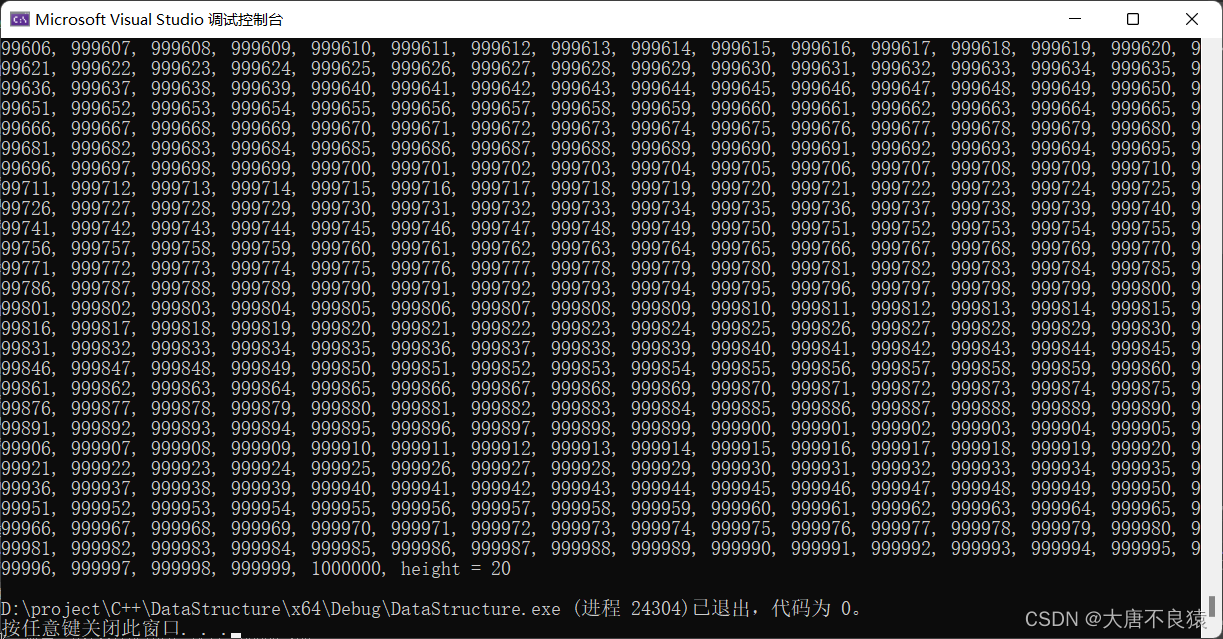
3.2.2.10.总结
1000000个结点,很快啊,只是全部遍历有点慢而已,插入和删除很快。
4.总结
建议多看视频,多看文章,B站上面的视频挺好的,刚开始也许不明白,但书读百遍,其意自现,我看了十几篇文章和七八个视频,当然有断断续续的看,有时间就看一点点,最后就知道怎么去实现了,实现只是在语言上有区别,思想没区别,而且语言相同,也只是写的方式不一样,也许有的语言可能比较方便。有的可能写起来比较简单,而有些复杂。
如果不知道思想,那建议多看几遍原理文章再找实现代码,或自己尝试写。
点赞加关注。
不懂可以评论处或私信,必回。
