文章目录
F.Sorting Pancakes
题意:
给你
n
(
n
≤
250
)
n(n\leq 250)
n(n≤250)个整数的序列
a
(
∑
a
i
≤
250
)
a(\sum a_i\leq250)
a(∑ai?≤250),你可以用
1
1
1的花费将
a
i
?
1
a_i-1
ai??1,使
a
i
+
1
a_{i+1}
ai+1?或
a
i
?
1
?
+
1
a_{i-1}\text{ }+1
ai?1??+1,问最小用多少的花费可将序列变为不上升序列
思路:
由于本题数据范围极小,于是想到费用流,但是由于最终变换出来的序列未知,所以无法实现
于是考虑对于每一个
a
i
a_i
ai?,最终其变为
b
i
b_i
bi?,
a
a
a的前缀和为
s
a
sa
sa,
b
b
b的前缀和为
s
b
sb
sb
如果写过糖果传递,一道与本题类似的题目,不难知道,最终的结果为
∑
∣
s
a
i
?
s
b
i
∣
\sum |sa_i-sb_i|
∑∣sai??sbi?∣
证明如下:
令
c
i
=
a
i
?
b
i
c_i=a_i-b_i
ci?=ai??bi?。在位置
1
1
1,我们需要
∣
c
1
∣
|c_1|
∣c1?∣次操作,如果
c
1
<
0
c_1<0
c1?<0表示位置
1
1
1向
2
2
2拿了
∣
c
1
∣
|c_1|
∣c1?∣个,反之,表示给了
c
1
c_1
c1?个
当到了位置
2
2
2,此时位置
2
2
2的数字应该是
a
2
+
a
1
?
b
1
a_2+a_1-b_1
a2?+a1??b1?,还应该操作
a
2
+
a
1
?
b
1
?
b
2
a_2+a_1-b_1-b_2
a2?+a1??b1??b2?来向位置
3
3
3多退少补
于是以此类推
i
=
1
????????????????????????????????????????????????
a
1
?
b
1
i
=
2
????????????????????????????????
a
1
?
b
1
+
a
2
?
b
2
i
=
3
???????????????
a
1
?
b
1
+
a
2
?
b
2
+
a
3
?
b
3
.
.
.
i=1 \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }a_1-b_1\\i=2 \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }a_1-b_1+a_2-b_2\\ \\i=3 \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }a_1-b_1+a_2-b_2+a_3-b_3 \\...
i=1????????????????????????????????????????????????a1??b1?i=2????????????????????????????????a1??b1?+a2??b2?i=3???????????????a1??b1?+a2??b2?+a3??b3?...
答案为
∑
∣
s
a
i
?
s
b
i
∣
\sum |sa_i-sb_i|
∑∣sai??sbi?∣
本题的正确解法为
D
P
DP
DP
定义
d
p
{
i
,
j
,
k
}
dp\{i,j,k\}
dp{i,j,k}表示在前
i
i
i个数中,前
i
i
i位之和为
j
j
j,第
i
i
i位上的数字为
k
k
k,此时前
i
i
i位数字需要的操作次数
如果第
i
?
1
i-1
i?1位数字为
p
p
p
d
p
[
i
]
[
j
]
[
k
]
=
d
p
[
i
?
1
]
[
j
?
k
]
[
p
]
+
a
b
s
(
s
a
i
?
s
b
i
)
dp[i][j][k]=dp[i-1][j-k][p]+abs(sa_i-sb_i)
dp[i][j][k]=dp[i?1][j?k][p]+abs(sai??sbi?)
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=2e5+7;
int f[255][255][255];
int a[255],sum[255];
int main()
{
memset(f,0x3f,sizeof(f));
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i];
if(n==1)
{
puts("0");return 0;
}
int ans=inf;
for(int i=0;i<=m;i++) f[1][i][i]=abs(a[1]-i);
for(int i=2;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int pre=0;pre<=j;pre++)
{
for(int k=0;k<=pre&&k+pre<=j;k++)
{
f[i][j][k]=min(f[i][j][k],f[i-1][j-k][pre]+abs(sum[i]-j));
if(i==n&&j==m) ans=min(ans,f[i][j][k]);
}
}
}
}
printf("%d\n",ans);
}
在此基础上还可以继续优化
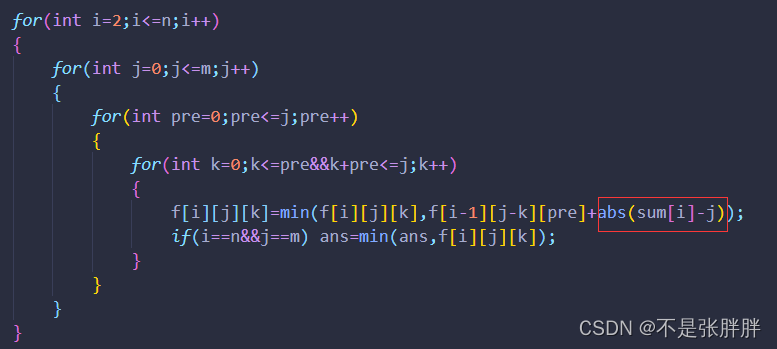
由于转移
d
p
{
i
,
j
,
k
}
dp\{i,j,k\}
dp{i,j,k}时,只与
∣
s
a
i
?
s
b
i
∣
|sa_i-sb_i|
∣sai??sbi?∣和
d
p
{
i
?
1
,
j
?
k
,
p
}
dp\{i-1,j-k,p\}
dp{i?1,j?k,p}有关,所以可以预处理
d
p
{
i
?
1
,
j
?
k
,
p
}
dp\{i-1,j-k,p\}
dp{i?1,j?k,p}最小后缀,来少一维循环,时间复杂度
O
(
n
3
)
O(n^3)
O(n3)
