[数据结构与算法]基于PGC相位生成载波调制及其解调算法实例分析

相较于其他类型的光纤传感器，目前人们普遍认为干涉型光纤传感器是最有发展前途的。干涉型光纤传感器属于相位调制型光纤传感器，它是以光纤中光的相位变化来表示被测信息，首先需要对光束进行干涉得到干涉信号，再对得到的干涉信号进行解调得到相位信息。无论此时传感器感知的被测信息是哪种物理现象：磁场、声场、还是温度、位移等，在理论上，干涉型光纤传感器都具有很高的灵敏度和分辨率，结构灵活多样，适用场合广泛。其基本传感原理为:当被测信息量作用于光纤，使得光纤内传播的光波的相位发生变化，再使用相位生成载波调制解调（phase generated carrier-PGC）这种相干解调技术将相位变化转换为光强变化，从而检测出待测的信息量。

一、PGC相位生成载波调制实现原理分析

如图所示外调制方式的PGC系统，干涉输出信号可以表示为

载波信号为$C\cos {\omega }_{0}t$，$\phi \left(t\right)$为待测信号和环境漂移共同引起的相位变化。$C\cos {\omega }_{0}t+\phi \left(t\right)$处于相位上，故将其看作相位变化，事实上载波信号和待测信号处于同等地位，由于载波频率远远高于待测信号，故可认为它载着待测信号，这就体现了相位载波的含义。

对式(1)进行贝塞尔函数展开得

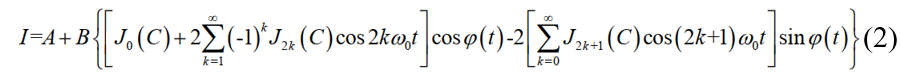
由式(2)可知，干涉输出信号I，当$\phi \left(t\right)=0$时，信号I中只存在${\omega }_0$的偶次谐波项；当$\phi \left(t\right)=\pi /2$时，信号I中只存在${\omega }_0$的奇次谐波项。$\phi \left(t\right)$可表示为

其中，$D\cos {\omega }_{s}t$为待测信号幅度， ${\phi }_0\left(t\right)$为环境噪声引起的相位变化。同理，$\cos \omega (t)$、$\sin \omega \left(t\right)$按贝塞尔函数展开

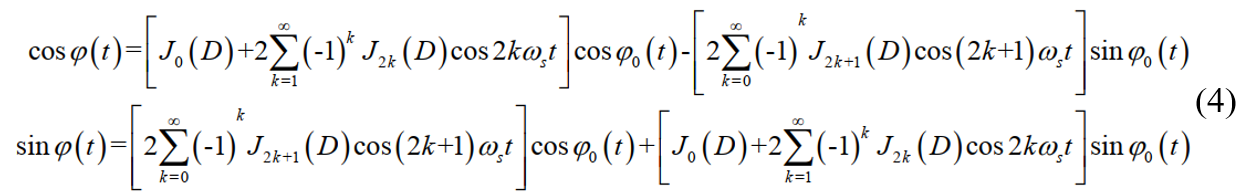
由式(4)可以看出，当${\phi }_0\left(t\right)=k\pi \begin{array}{cc}& (k=012?)\end{array}$时，输出干涉信号频谱中，偶（奇）次角频率${\omega }_s$出现在偶（奇）次角频率${\omega }_0$的两侧；当${\phi }_0\left(t\right)=k\pi +\pi /2\begin{array}{cc}& (k=012?)\end{array}$时，频谱上偶（奇）次角频率${\omega }_s$出现在奇（偶）次角频率${\omega }_0$的两侧，待测信号的信息包含在奇（偶）次角频率${\omega }_0$的两侧的边带频谱中，它们或以${\omega }_0$偶次角频率，或以${\omega }_0$奇次角频率为中心。从而实现了相位生成载波调制。

未加载波调制前，当$\phi \left(t\right)=k\pi \begin{array}{cc}& (k=012?)\end{array}$时，$\cos \omega t=\pm 1$；$\phi \left(t\right)=k\pi +\pi /2\begin{array}{cc}& (k=012?)\end{array}$时，$\cos \omega t=0$。此时干涉信号将发生消隐或畸变，无法从中解调将待测信号。根据以上分析，加入载波信号后，即使出现$\phi \left(t\right)=k\pi$或$\phi \left(t\right)=k\pi +\pi /2$也不会发生信号的消隐或畸变，从而实现抗相位衰落。这就是进行相位生成载波调制的原因和意义所在。

二、PGC解调算法原理分析及相关参数选取

传统的PGC解调算法分为微分交叉相乘（DCM）算法和反正切（Arctan）算法两种。以下将分别对两种解调算法进行详细分析，并分别对两种算法中的一些参数的选取原则进行详细的理论分析，如最佳相位调制度的选取、系统最低采样频率及系统解调动态范围上限等。

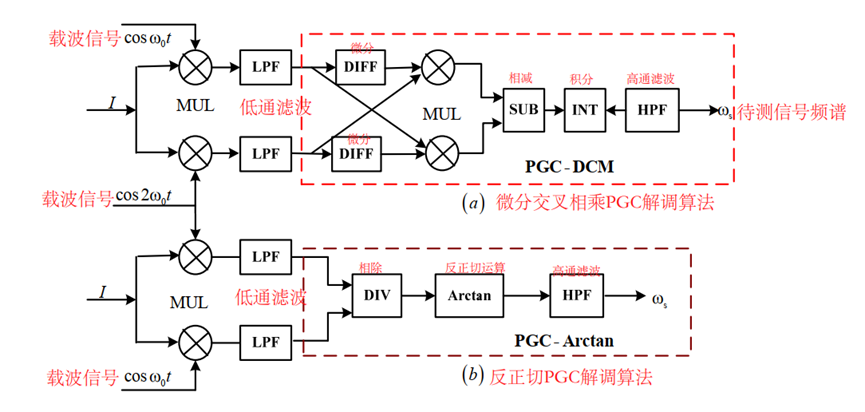
2.1 微分交叉相乘DCM解调算法原理

DCM 解调算法的思路是将干涉信号分别与单倍频和二倍频混频低通滤波后，得到一对相互正交的余弦项和正弦项，然后再经过微分交叉相乘相减、积分、高通滤波后实现待测信号的解调。具体过程如下：干涉信号分别与幅度分别为G、H，角频率为${\omega }_0$和$2{\omega }_0$的载波混频、低通滤波后得到

经过微分交叉相乘相减积分处理后的信号为

再通过高通滤波器得到了待测信号，即DCM算法解调输出为

待测信号被解调出来，只是幅值变化了一个系数$B^{2}GH{J}_1\left(C\right)J_2\left(C\right)$ 。为了减小输出结果对贝塞尔函数的依赖关系，通过选择适当的载波信号幅度即相位调制度C，使得 $J_1\left(C\right)J_2\left(C\right)$取得极大值，且当C值稍有变化时系统解调输出幅值变化不大，再可以通过幅度补偿实现待测信号的完全解调。

2.2 Arctan 解调算法

Arctan 算法与 DCM 算法相同之处在于：二者都是分别与单倍频和二倍频混频低通滤波后得到两个相互正交的余弦项和正弦项。不同之处在于：反正切算法是将得到的两个正交项进行除法运算得到正切信号，然后对正切信号进行反正切算法，最后经过高通滤波实现信号的解调。

具体分析过程如下：干涉信号与载波混频低通后得到的正交项

对两式相除后得到
求反正切再经高通滤波后得到

实现对待测信号的解调。

三、实例验证

3.1 Arctan反正切解调算法验证

首先分别模拟生成调制信号，与待测信号，并对待测信号添加噪声后进行调制，得到的调制信号如下图所示：

采用反正切解调算法进行解调，结果如下图所示：

该Matlab程序资源，可从下方获取

https://download.csdn.net/download/qq_36584460/85322776
下载后如有程序运行问题，请及时联系博主。

3.2 微分交叉相乘DCM解调算法实例演示

首先分别模拟生成调制信号，与待测信号，并对待测信号添加噪声后进行调制，得到的调制信号如下图所示：

采用微分交叉相乘DCM解调算法进行解调，结果如下图所示：

该Matlab程序资源，可从下方获取：

https://download.csdn.net/download/qq_36584460/85322781

下载后如有程序运行问题，请及时联系博主。

四、Labview用户界面

最后，开发了基于PGC相位生成载波调制及其解调的labview用户界面，如有需要，可私信博主。

五、参考文献

王燕. 干涉型光纤传感器及PGC解调技术研究, 天津理工大学, (2014).

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖