1、平衡二叉树
????????平衡二叉树(Self-Balancing Binary Search Tree 或 Height-Balanced Binary Search Tree)是树的一种特殊的结构。平衡二叉树的组成条件是必须是二叉排序树,且高度平衡。
- ? 二叉排序树?
一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
(2)若右子树不空,则右子树上所有节点的值均大于它的根节点的值;
(3)左、右子树也分别为二叉排序树;
【注】:没有键值相等的节点。
- 高度平衡
(1)一棵空树;
(2)或它的左子树和右子树都是平衡二叉树;
(3)且左子树和右子树的深度差的绝对值不超过1。
【注】:二叉树上节点的左子树深度减去右子树深度的值称为平衡因子BF(Balance Factor)。
2、平衡二叉树的操作
? 当插入或删除元素时,会破坏二叉树的平衡。通过以下4种操作,可以恢复平衡:
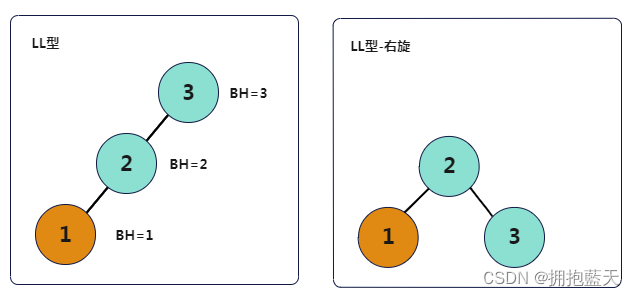
LL型:插入左节点的左子树,右旋。
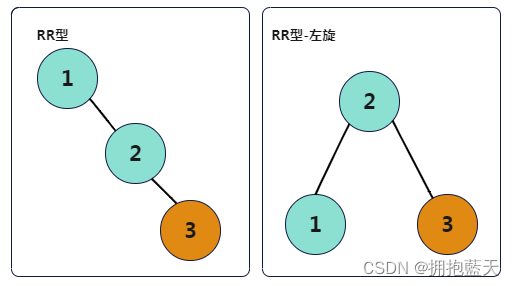
RR型:插入右节点的右子树,左旋。
?
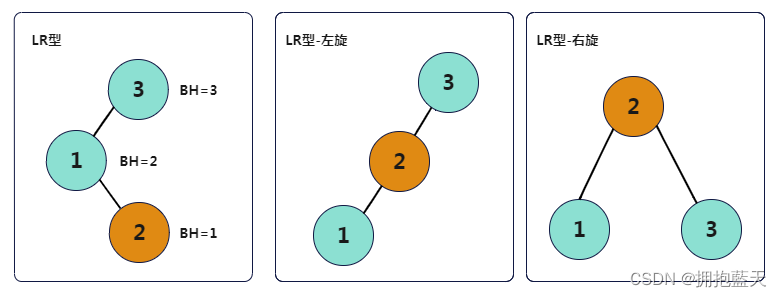
LR型:插入左节点的右子树,先左旋,再右旋。
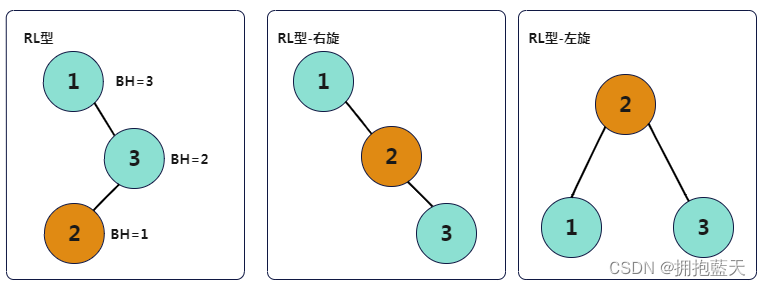
RL型:插入右节点的左子树,先右旋,再左旋。
?3、测试代码
#include <stdio.h>
#include <malloc.h>
#include <string.h>
#include <stdlib.h>
typedef struct BinaryNode{
int iValue;
int iHeight;
struct BinaryNode *pstLeft;
struct BinaryNode *pstRight;
}BINARY_NODE_S;
int getNodeHeight(BINARY_NODE_S *pstNode)
{
if(NULL == pstNode)
{
return 0;
}
else
{
return pstNode->iHeight;
}
}
int getNodeMaxHeight(BINARY_NODE_S *pstNode)
{
int iLeftHeight;
int iRightHeight;
iLeftHeight = getNodeHeight(pstNode->pstLeft);
iRightHeight = getNodeHeight(pstNode->pstRight);
return iLeftHeight > iRightHeight ? iLeftHeight : iRightHeight;
}
BINARY_NODE_S *rotateRight(BINARY_NODE_S *pstRoot)
{
BINARY_NODE_S *pstNode;
pstNode = pstRoot->pstLeft;
pstRoot->pstLeft = pstNode->pstRight;
pstNode->pstRight = pstRoot;
pstRoot->iHeight = getNodeMaxHeight(pstRoot) + 1;
pstNode->iHeight = getNodeMaxHeight(pstNode) + 1;
return pstNode;
}
BINARY_NODE_S *rotateLeft(BINARY_NODE_S *pstRoot)
{
BINARY_NODE_S *pstNode;
pstNode = pstRoot->pstRight;
pstRoot->pstRight = pstNode->pstLeft;
pstNode->pstLeft = pstRoot;
pstRoot->iHeight = getNodeMaxHeight(pstRoot) + 1;
pstNode->iHeight = getNodeMaxHeight(pstNode) + 1;
return pstNode;
}
BINARY_NODE_S *rotateLeftRight(BINARY_NODE_S *pstRoot)
{
pstRoot->pstLeft = rotateLeft(pstRoot->pstLeft);
return rotateRight(pstRoot);
}
BINARY_NODE_S *rotateRightLeft(BINARY_NODE_S *pstRoot)
{
pstRoot->pstRight = rotateRight(pstRoot->pstRight);
return rotateLeft(pstRoot);
}
BINARY_NODE_S *addNode(BINARY_NODE_S *pstRoot, int iValue)
{
int iLeftHeight;
int iRightHeight;
if(NULL == pstRoot)
{
pstRoot = (BINARY_NODE_S *)malloc(sizeof(BINARY_NODE_S));
pstRoot->iValue = iValue;
pstRoot->iHeight = 1;
pstRoot->pstLeft = NULL;
pstRoot->pstRight = NULL;
}
else if(iValue < pstRoot->iValue)
{
pstRoot->pstLeft = addNode(pstRoot->pstLeft, iValue);
pstRoot->iHeight = getNodeMaxHeight(pstRoot) + 1;
iLeftHeight = getNodeHeight(pstRoot->pstLeft);
iRightHeight = getNodeHeight(pstRoot->pstRight);
if(2 == iLeftHeight - iRightHeight)
{
if(iValue < pstRoot->pstLeft->iValue)
{
printf("Left-Left: Right rotate.\n");
pstRoot = rotateRight(pstRoot);
}
else
{
printf("Left-Righ: Left and right rotate.\n");
pstRoot = rotateLeftRight(pstRoot);
}
}
else
{
printf("Left add.\n");
}
}
else
{
pstRoot->pstRight = addNode(pstRoot->pstRight, iValue);
pstRoot->iHeight = getNodeMaxHeight(pstRoot) + 1;
iLeftHeight = getNodeHeight(pstRoot->pstLeft);
iRightHeight = getNodeHeight(pstRoot->pstRight);
if(-2 == iLeftHeight - iRightHeight)
{
if(iValue > pstRoot->pstRight->iValue)
{
printf("Right-Right: Left rotate.\n");
pstRoot = rotateLeft(pstRoot);
}
else
{
printf("Right-Left: Right and left rotate.\n");
pstRoot = rotateRightLeft(pstRoot);
}
}
else
{
printf("Right add.\n");
}
}
return pstRoot;
}
/* 释放树:后序 */
void deInitTree(BINARY_NODE_S *pstRoot)
{
if(NULL != pstRoot)
{
deInitTree(pstRoot->pstLeft);
deInitTree(pstRoot->pstRight);
free(pstRoot);
}
}
/* 遍历树:前序 */
void scanTreePre(BINARY_NODE_S *pstRoot)
{
if(NULL != pstRoot)
{
printf("%d ", pstRoot->iValue);
scanTreePre(pstRoot->pstLeft);
scanTreePre(pstRoot->pstRight);
}
}
/* 遍历树:中序 */
void scanTreeIn(BINARY_NODE_S *pstRoot)
{
if(NULL != pstRoot)
{
scanTreeIn(pstRoot->pstLeft);
printf("%d ", pstRoot->iValue);
scanTreeIn(pstRoot->pstRight);
}
}
/* 遍历树:后序 */
void scanTreePost(BINARY_NODE_S *pstRoot)
{
if(NULL != pstRoot)
{
scanTreePost(pstRoot->pstLeft);
scanTreePost(pstRoot->pstRight);
printf("%d ", pstRoot->iValue);
}
}
/* 创建树 */
BINARY_NODE_S *InitTree(void)
{
int auiDate[] ={3,2,1,4,5,6,7,10,9,8};
BINARY_NODE_S *pstRoot = NULL;
for(int i=0; i<sizeof(auiDate)/sizeof(auiDate[0]); ++i)
{
printf("\n====== Add: %d\n", auiDate[i]);
pstRoot = addNode(pstRoot, auiDate[i]);
printf("Tree: ");
scanTreePre(pstRoot);
printf("\n");
}
return pstRoot;
}
int main()
{
BINARY_NODE_S *pstRoot;
pstRoot = InitTree();
printf("\nPre: ");
scanTreePre(pstRoot);
printf("\n");
printf("In: ");
scanTreeIn(pstRoot);
printf("\n");
printf("Post: ");
scanTreePost(pstRoot);
printf("\n");
deInitTree(pstRoot);
return 0;
}
?4、测试log
====== Add: 3
Tree: 3
====== Add: 2
Left add.
Tree: 3 2
====== Add: 1
Left add.
Left-Left: Right rotate.
Tree: 2 1 3
====== Add: 4
Right add.
Right add.
Tree: 2 1 3 4
====== Add: 5
Right add.
Right-Right: Left rotate.
Right add.
Tree: 2 1 4 3 5
====== Add: 6
Right add.
Right add.
Right-Right: Left rotate.
Tree: 4 2 1 3 5 6
====== Add: 7
Right add.
Right-Right: Left rotate.
Right add.
Tree: 4 2 1 3 6 5 7
====== Add: 10
Right add.
Right add.
Right add.
Tree: 4 2 1 3 6 5 7 10
====== Add: 9
Left add.
Right-Left: Right and left rotate.
Right add.
Right add.
Tree: 4 2 1 3 6 5 9 7 10
====== Add: 8
Right add.
Left add.
Right-Left: Right and left rotate.
Right add.
Tree: 4 2 1 3 7 6 5 9 8 10
Pre: 4 2 1 3 7 6 5 9 8 10
In: 1 2 3 4 5 6 7 8 9 10
Post: 1 3 2 5 6 8 10 9 7 4
?5、最终创建二叉树
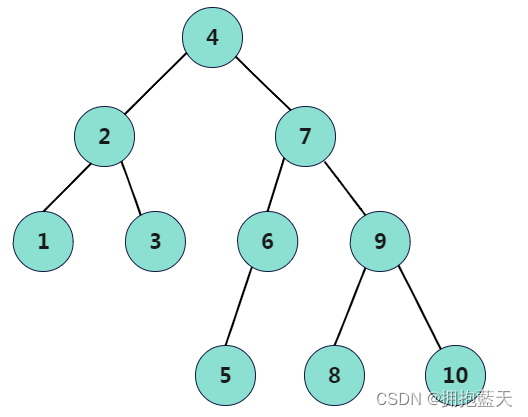
6、算法分析
- 搜索时间效率为O(log n);
- 频繁的插入和删除,会引起频繁的旋转,导致效率下降;