目录
题目
????????给你一棵二叉树的根节点 root ,找出并返回满足要求的节点数,要求节点的值等于其 子树 中值的 平均值 。
注意:
n 个元素的平均值可以由 n 个元素 求和 然后再除以 n ,并 向下舍入 到最近的整数。
root 的 子树 由 root 和它的所有后代组成。
?
示例 1:
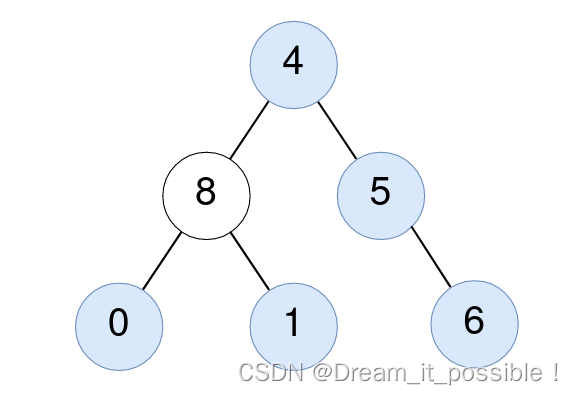
输入:root = [4,8,5,0,1,null,6]
输出:5
解释:
对值为 4 的节点:子树的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。
对值为 5 的节点:子树的平均值 (5 + 6) / 2 = 11 / 2 = 5 。
对值为 0 的节点:子树的平均值 0 / 1 = 0 。
对值为 1 的节点:子树的平均值 1 / 1 = 1 。
对值为 6 的节点:子树的平均值 6 / 1 = 6 。
示例 2:
输入:root = [1]
输出:1
解释:对值为 1 的节点:子树的平均值 1 / 1 = 1。
提示:
树中节点数目在范围 [1, 1000] 内
0 <= Node.val <= 1000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-nodes-equal-to-average-of-subtree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
解题关键
1.? 求解每个节点的所有子节点的和,包含自身节点。
2.? 求解每个节点的所有子节点的个数,包含自身节点。
3.? ?采用后序遍历算法模型,将每一个节点和子节点的看做后序遍历的一个整体。
4.? ?后序遍历,采用递归解法。
后序遍历算法
? ? ? ? 打印按照左、右、中的顺序输出,通过递归实现:
public static void postTraverseTree(TreeNode root) {
if (root == null) {
return;
}
if (root.left != null)
postTraverseTree(root.left);
if (root.right != null)
postTraverseTree(root.right);
System.out.println(root.val);
}? ? ? ? 定义一个数组:? arg1 为当前节点的子树+本身的值和,arg2为当前节点+子树的个数和,arg3为满足平均值的节点个数。
? ? ? ? 计算每次递归的子节点和、子节点个数然后重新赋值到int[0]和int[1]里,为下次递归计算子节点和、子节点个数做准备。Int[2]为满足条件的节点数,最终值为题目需要的结果。
private int[] dfs(TreeNode root) {
if (root == null) {
// arg1 为当前节点的子树+本身的值和,arg2为当前节点+子树的个数和,arg3为满足平均值的节点个数。
return new int[]{0, 0, 0};
}
int[] arrLeft = dfs(root.left);
int[] arrRight = dfs(root.right);
// 获取到子树节点总和
int sum = arrLeft[0] + arrRight[0] + root.val;
// 获取子节点个数,含本身
int nums = arrLeft[1] + arrRight[1] + 1;
int avg = sum / nums;
int target = arrLeft[2] + arrRight[2];
// 如果满足条件,那么target++, 并重新赋值到数组里。
if (avg == root.val) {
target++;
}
return new int[]{sum, nums, target};
}完整代码?
package leetcode100.BTree;
import java.util.Deque;
import java.util.Queue;
import java.util.Stack;
import java.util.concurrent.LinkedBlockingDeque;
import java.util.concurrent.LinkedBlockingQueue;
/**
* @Desc:
* @Author: bingbing
* @Date: 2022/5/8 0008 15:54
* 给你一棵二叉树的根节点 root ,找出并返回满足要求的节点数,要求节点的值等于其 子树 中值的 平均值 。
* <p>
* 注意:
* <p>
* n 个元素的平均值可以由 n 个元素 求和 然后再除以 n ,并 向下舍入 到最近的整数。
* root 的 子树 由 root 和它的所有后代组成。
* <p>
* <p>
* 示例 1:
* <p>
* <p>
* 输入:root = [4,8,5,0,1,null,6]
* 输出:5
* 解释:
* 对值为 4 的节点:子树的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。
* 对值为 5 的节点:子树的平均值 (5 + 6) / 2 = 11 / 2 = 5 。
* 对值为 0 的节点:子树的平均值 0 / 1 = 0 。
* 对值为 1 的节点:子树的平均值 1 / 1 = 1 。
* 对值为 6 的节点:子树的平均值 6 / 1 = 6 。
* 示例 2:
* <p>
* <p>
* 输入:root = [1]
* 输出:1
* 解释:对值为 1 的节点:子树的平均值 1 / 1 = 1。
*/
public class AverageSubTreeProblem6057 {
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
public TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "TreeNode{" +
"val=" + val +
'}';
}
}
/**
* @param root 根节点
* @return 满足节点个数
*/
public int averageOfSubtree0(TreeNode root) {
int target = 0;
if (root.left == null && root.right == null) {
return 1;
}
// 节点栈
Deque<TreeNode> queue = new LinkedBlockingDeque<>();
// // 子节点和栈
// Deque<In>
// 节点总个数
int rootSubTreeSums = 1;
// 节点总和
int treeSums = root.val;
while (!queue.isEmpty()) {
TreeNode node = queue.peek();
// 子树和
int subTreeSums = 0;
if (node.right != null) {
queue.add(node.right);
// subTreeSums += node.right.val;
// rootSubTreeSums++;
}
if (node.left != null) {
queue.add(node.left);
// subTreeSums += node.left.val;
// rootSubTreeSums++;
}
// treeSums += rootSubTreeSums;
// if (subTreeSums / subTreeSums == node.val) {
//
// }
}
// if ((treeSums / rootSubTreeSums) == root.val) {
// target++;
// }
return target;
}
public int averageOfSubtree(TreeNode root) {
return dfs(root)[2];
}
private int[] dfs(TreeNode root) {
if (root == null) {
return new int[]{0, 0, 0};
}
int[] arrLeft = dfs(root.left);
int[] arrRight = dfs(root.right);
int sum = arrLeft[0] + arrRight[0] + root.val;
int nums = arrLeft[1] + arrRight[1] + 1;
int avg = sum / nums;
int target = arrLeft[2] + arrRight[2];
if (avg == root.val) {
target++;
}
return new int[]{sum, nums, target};
}
/**
* 后序遍历算法
*
* @param root
*/
public static void postTraverseTree(TreeNode root) {
if (root == null) {
return;
}
if (root.left != null)
postTraverseTree(root.left);
if (root.right != null)
postTraverseTree(root.right);
System.out.println(root.val);
}
public static void main(String[] args) {
AverageSubTreeProblem6057 subTreeProblem6057 = new AverageSubTreeProblem6057();
TreeNode root = new TreeNode(1, new TreeNode(2, new TreeNode(4, null, new TreeNode(6, null, null)), new TreeNode(5, null, null)), new TreeNode(3, null, null));
// 后序遍历
postTraverseTree(root);
int nums = subTreeProblem6057.averageOfSubtree(root);
System.out.println("结果为: " + nums);
}
}
?提交结果:
时间复杂度和空间复杂度?
? ? ? ? 由于是后序遍历算法,时间复杂度为O(N), 调用系统栈空间复杂度为O(N)。
