原文链接:LeetCode热题Top100 | 简单
1.两数之和(1)
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1]
func twoSum1(nums []int, target int) []int {
for i, v := range nums{
for j := i + 1; j < len(nums); j++ {
sum := v + nums[j]
if sum == target {
return []int{i, j}
}
}
}
return nil
}
func twoSum2(nums []int, target int) []int {
mapTemp := make(map[int]int, len(nums))
for i, v := range nums {
if j, ok := mapTemp[target-v]; ok {
return []int{j, i}
}
mapTemp[v] = i
}
return nil
}
func main() {
nums := []int{2, 7, 11, 15}
target := 9
result1 := twoSum1(nums, target)
fmt.Println(result1)
result2 := twoSum2(nums, target)
fmt.Println(result2)
}
2.有效的括号(20)
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
示例 1:
输入:s = "()[]{}"
输出:true
示例 2:
输入:s = "{[]}"
输出:true
示例 3:
输入:s = "([)]"
输出:false
func isValid(s string) bool {
if len(s)%2 == 1 {
return false
}
mapTemp := map[byte]byte{
')': '(',
']': '[',
'}': '{',
}
var stack []byte
for i := 0; i < len(s); i++ {
if v, ok := mapTemp[s[i]]; ok {
if len(stack) == 0 || stack[len(stack)-1] != v {
return false
}
stack = stack[:len(stack)-1]
} else {
stack = append(stack, s[i])
}
}
return len(stack) == 0
}
func main() {
s := "()[]{}"
b := isValid(s)
fmt.Println(b)
}
3.合并两个有序链表(21)
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例1:
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
type ListNode struct {
Val int
Next *ListNode
}
func mergeTwoLists1(l1 *ListNode, l2 *ListNode) *ListNode {
if l1 == nil {
return l2
}
if l2 == nil {
return l1
}
var result *ListNode
if l1.Val <= l2.Val {
result = l1
result.Next = mergeTwoLists1(l1.Next, l2)
} else {
result = l2
result.Next = mergeTwoLists1(l1, l2.Next)
}
return result
}
func mergeTwoLists2(l1 *ListNode, l2 *ListNode) *ListNode {
nodeTemp := &ListNode{}
current := nodeTemp
for l1 != nil && l2 != nil {
if l1.Val < l2.Val {
current.Next = l1
l1 = l1.Next
} else {
current.Next = l2
l2 = l2.Next
}
current = current.Next
}
if l1 != nil {
current.Next = l1
} else {
current.Next = l2
}
return nodeTemp.Next
}
func main() {
var h1 = new(ListNode)
h1.Val = 1
var h2 = new(ListNode)
h2.Val = 2
var h3 = new(ListNode)
h3.Val = 4
h1.Next = h2
h2.Next = h3
h3.Next = nil
var h11 = new(ListNode)
h11.Val = 1
var h22 = new(ListNode)
h22.Val = 3
var h33 = new(ListNode)
h33.Val = 4
h11.Next = h22
h22.Next = h33
h33.Next = nil
result2 := mergeTwoLists2(h1, h11)
fmt.Println(result2)
}
4.最大子序和(53)
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6
示例 2:
输入:nums = [1]
输出:1
func maxSubArray(nums []int) int {
max := nums[0]
for i := 1; i < len(nums); i++ {
if nums[i-1]+nums[i] > nums[i] {
nums[i] += nums[i-1]
}
if max < nums[i] {
max = nums[i]
}
}
return max
}
func main() {
nums := []int{-2, 1, -3, 4, -1, 2, 1, -5, 4}
result := maxSubArray(nums)
fmt.Println(result)
}
5.爬楼梯(70)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
func climbStairs1(n int) int {
if n == 1 {
return 1
}
if n == 2 {
return 2
}
return climbStairs1(n-1) + climbStairs1(n-2)
}
func climbStairs2(n int) int {
memo := make([]int, n+1, n+1)
return climbStairsMemo(n, memo)
}
func climbStairsMemo(n int, memo []int) int {
if memo[n] > 0 {
return memo[n]
}
if n == 1 {
memo[n] = 1
} else if n == 2 {
memo[n] = 2
} else {
memo[n] = climbStairsMemo(n-1, memo) + climbStairsMemo(n-2, memo)
}
return memo[n]
}
func climbStairs3(n int) int {
p, q, r := 0, 0, 1
for i := 0; i < n; i++ {
p = q
q = r
r = p + q
}
return r
}
func main() {
n := 10
result1 := climbStairs1(n)
fmt.Println(result1)
result2 := climbStairs2(n)
fmt.Println(result2)
result3 := climbStairs3(n)
fmt.Println(result3)
}
6.二叉树的中序遍历(94)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func inorderTraversal1(root *TreeNode) (res []int) {
var inorder func(node *TreeNode)
inorder = func(node *TreeNode) {
if node != nil {
inorder(node.Left)
res = append(res, node.Val)
inorder(node.Right)
}
return
}
inorder(root)
return
}
func inorderTraversal2(root *TreeNode) (res []int) {
var stack []*TreeNode
for root != nil || len(stack) > 0 {
for root != nil {
stack = append(stack, root)
root = root.Left
}
root = stack[len(stack)-1]
stack = stack[:len(stack)-1]
res = append(res, root.Val)
root = root.Right
}
return
}
func main() {
var root = new(TreeNode)
var root1 = new(TreeNode)
var root2 = new(TreeNode)
root.Val = 1
root.Left = nil
root.Right = root1
root1.Val = 2
root1.Right = nil
root1.Left = root2
root2.Val = 3
root2.Left = nil
root2.Right = nil
a := inorderTraversal1(root)
fmt.Println(a)
b := inorderTraversal2(root)
fmt.Println(b)
}
7.对称二叉树(101)
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个[1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func isSymmetric1(root *TreeNode) bool {
return check(root, root)
}
func check(p, q *TreeNode) bool {
if p == nil && q == nil {
return true
}
if p == nil || q == nil {
return false
}
return p.Val == q.Val && check(p.Left, q.Right) && check(p.Right, q.Left)
}
func isSymmetric2(root *TreeNode) bool {
u, v := root, root
var queue []*TreeNode
queue = append(queue, u)
queue = append(queue, v)
for len(queue) > 0 {
u, v = queue[0], queue[1]
queue = queue[2:]
if u == nil && v == nil {
continue
}
if u == nil || v == nil {
return false
}
if u.Val != v.Val {
return false
}
queue = append(queue, u.Left)
queue = append(queue, v.Right)
queue = append(queue, u.Right)
queue = append(queue, v.Left)
}
return true
}
func main() {
var n1 = new(TreeNode)
var n2 = new(TreeNode)
var n3 = new(TreeNode)
var n4 = new(TreeNode)
var n5 = new(TreeNode)
var n6 = new(TreeNode)
var n7 = new(TreeNode)
n1.Val = 1
n2.Val = 2
n3.Val = 2
n4.Val = 3
n5.Val = 4
n6.Val = 4
n7.Val = 3
n1.Left = n2
n1.Right = n3
n2.Left = n4
n2.Right = n5
n3.Left = n6
n3.Right = n7
result1 := isSymmetric1(n1)
fmt.Println(result1)
result2 := isSymmetric2(n1)
fmt.Println(result2)
}
8.二叉树的最大深度(104)
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明:叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度3
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func max(a, b int) int {
if a < b {
return b
}
return a
}
func maxDepth(root *TreeNode) int {
if root == nil {
return 0
}
return max(maxDepth(root.Left), maxDepth(root.Right)) + 1
}
func maxDepth1(root *TreeNode) int {
if root == nil {
return 0
}
var queue []*TreeNode
queue = append(queue, root)
ans := 0
for len(queue) > 0 {
sz := len(queue)
for sz > 0 {
node := queue[0]
queue = queue[1:]
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
sz--
}
ans++
}
return ans
}
func main() {
var root = new(TreeNode)
var root1 = new(TreeNode)
var root2 = new(TreeNode)
var root3 = new(TreeNode)
var root4 = new(TreeNode)
root.Val = 3
root.Left = root1
root.Right = root2
root1.Val = 9
root2.Val = 20
root2.Left = root3
root2.Right = root4
root3.Val = 15
root4.Val = 7
fmt.Println(maxDepth(root))
fmt.Println(maxDepth1(root))
}
9.买卖股票的最佳时机(121)
给定一个数组 prices ,它的第i 个元素prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
func maxProfit(prices []int) int {
maxNum := 0
tempMaxNum := 0
min := prices[0]
for i := 1; i < len(prices); i++ {
if prices[i] < min {
min = prices[i]
}
tempMaxNum = prices[i] - min
if tempMaxNum > maxNum {
maxNum = tempMaxNum
}
}
return maxNum
}
func main() {
prices := []int{7, 1, 5, 3, 6, 4}
fmt.Println(maxProfit(prices))
pricess := []int{7, 6, 4, 3, 1, 0}
fmt.Println(maxProfit(pricess))
fmt.Println(math.MaxInt64)
fmt.Println(math.MinInt64)
}
10.只出现一次的数字(136)
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例2:
输入: [4,1,2,1,2]
输出: 4
func singleNumber(nums []int) int {
repeate := make(map[int]bool)
for i := 0; i < len(nums); i++ {
_, exist := repeate[nums[i]]
if exist {
repeate[nums[i]] = true
} else {
repeate[nums[i]] = false
}
}
for i := 0; i < len(nums); i++ {
if repeate[nums[i]] == false {
return nums[i]
}
}
return 0
}
func singleNumber1(nums []int) int {
repeate := make(map[int]bool)
final := 0
for i := 0; i < len(nums); i++ {
if _, exist := repeate[nums[i]]; !exist {
repeate[nums[i]] = true
final += nums[i]
} else {
final -= nums[i]
}
}
return final
}
func singleNumber2(nums []int) int {
s := 0
for i:=0; i<len(nums); i++ {
s = s ^ nums[i]
}
return s
}
func main() {
a := []int{4, 1, 2, 1, 2}
fmt.Println(singleNumber(a))
fmt.Println(singleNumber1(a))
fmt.Println(singleNumber2(a))
}
11.环形链表(141)
给一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。
为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。
注意:pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
示例:
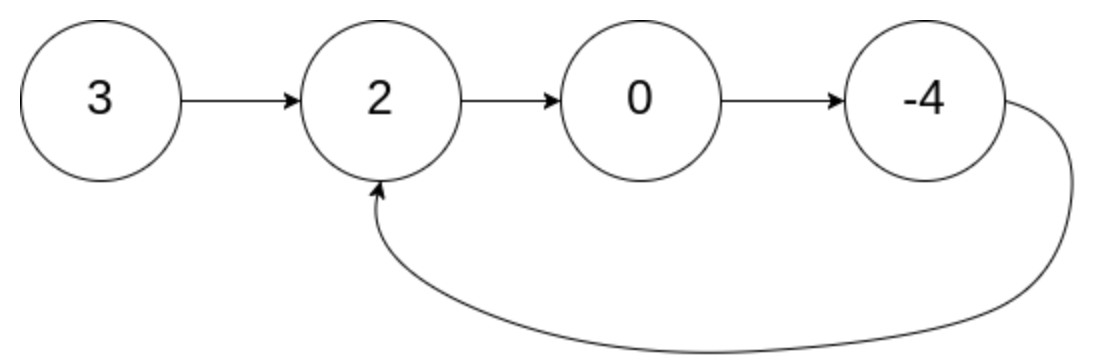
输入:head = [3,2,0,-4],pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点
type ListNode struct {
Val int
Next *ListNode
}
func hasCycle1(head *ListNode) bool {
tempMap := map[*ListNode]struct{}{}
for head != nil {
if _, ok := tempMap[head]; ok {
return true
}
tempMap[head] = struct{}{}
head = head.Next
}
return false
}
func hasCycle2(head *ListNode) bool {
if head == nil || head.Next == nil {
return false
}
slow, fast := head, head.Next
for slow != fast {
if fast == nil || fast.Next == nil {
return false
}
slow = slow.Next
fast = fast.Next.Next
}
return true
}
func main() {
node1 := new(ListNode)
node2 := new(ListNode)
node3 := new(ListNode)
node4 := new(ListNode)
node1.Val = 3
node1.Next = node2
node2.Val = 2
node2.Next = node3
node3.Val = 0
node3.Next = node4
node4.Val = -4
node4.Next = node2
cycle1 := hasCycle1(node1)
fmt.Println(cycle1)
cycle2 := hasCycle2(node1)
fmt.Println(cycle2)
}
12.最小栈(155)
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop()—— 删除栈顶的元素。
top()—— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
思路:
对于栈来说,如果一个元素 a 在入栈时,栈里有其它的元素 b, c, d,那么无论这个栈在之后经历了什么操作,
只要 a 在栈中,b, c, d 就一定在栈中,因为在 a 被弹出之前,b, c, d 不会被弹出。
因此,在操作过程中的任意一个时刻,只要栈顶的元素是 a,那么就可以确定栈里面现在的元素一定是 a, b, c, d。
那么,可以在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时,如果栈顶元素是 a,
就可以直接返回存储的最小值 m
type MinStack struct {
stack []int
minStack []int
}
func Constructor() MinStack {
return MinStack{
stack: []int{},
minStack: []int{math.MaxInt64},
}
}
func (this *MinStack) Push(x int) {
this.stack = append(this.stack, x)
top := this.minStack[len(this.minStack)-1]
this.minStack = append(this.minStack, min(x, top))
}
func (this *MinStack) Pop() {
this.stack = this.stack[:len(this.stack)-1]
this.minStack = this.minStack[:len(this.minStack)-1]
}
func (this *MinStack) Top() int {
return this.stack[len(this.stack)-1]
}
func (this *MinStack) GetMin() int {
return this.minStack[len(this.minStack)-1]
}
func min(x, y int) int {
if x < y {
return x
}
return y
}
func main() {
}
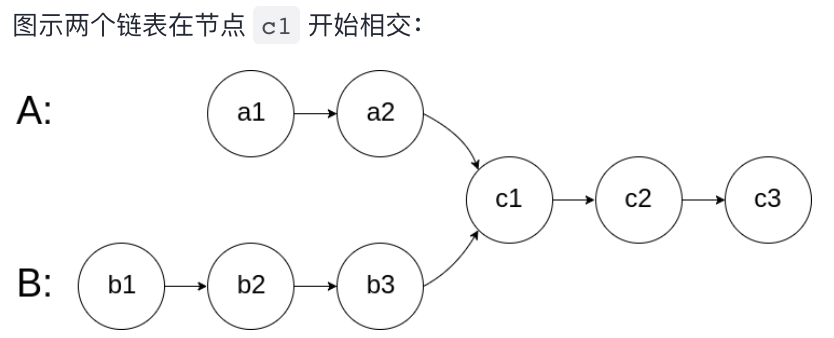
13.相交链表(160)
给两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点,
如果两个链表不存在相交节点,返回 null。
题目保证整个链式结构中不存在环,且函数返回结果后,链表必须保持其原始结构
设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案
type ListNode struct {
Val int
Next *ListNode
}
func getIntersectionNode1(headA, headB *ListNode) *ListNode {
tempMap := map[*ListNode]bool{}
for tmp := headA; tmp != nil; tmp = tmp.Next {
tempMap[tmp] = true
}
for tmp := headB; tmp != nil; tmp = tmp.Next {
if tempMap[tmp] {
return tmp
}
}
return nil
}
func getIntersectionNode2(headA, headB *ListNode) *ListNode {
if headA == nil || headB == nil {
return nil
}
pa, pb := headA, headB
for pa != pb {
if pa == nil {
pa = headB
} else {
pa = pa.Next
}
if pb == nil {
pb = headA
} else {
pb = pb.Next
}
}
return pa
}
func main() {
}
14.多数元素(169)
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于? n/2 ?的元素。
可以假设数组是非空的,并且给定的数组总是存在多数元素。
设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题
示例1:
输入:[3,2,3]
输出:3
示例2:
输入:[2,2,1,1,1,2,2]
输出:2
func majorityElement1(nums []int) int {
tempMap := map[int]int{}
max := math.MinInt
final := 0
for _, v := range nums {
if _, ok := tempMap[v]; ok {
tempMap[v]++
} else {
tempMap[v] = 1
}
}
for k, v := range tempMap {
if v > max {
max = v
final = k
}
}
return final
}
func majorityElement2(nums []int) int {
sort.Ints(nums)
return nums[len(nums)/2]
}
func majorityElement3(nums []int) int {
for {
randIndex := rand.Intn(len(nums))
candidate := nums[randIndex]
count := 0
for i := 0; i < len(nums); i++ {
if nums[i] == candidate {
count++
if count > len(nums)/2 {
return nums[i]
}
}
}
}
}
func majorityElement4(nums []int) int {
count := 0
candidate := 0
for i := 0; i < len(nums); i++ {
if count == 0 {
candidate = nums[i]
}
if candidate == nums[i] {
count++
} else {
count--
}
}
return candidate
}
func main() {
s := []int{2, 2, 1, 1, 1, 2, 2}
fmt.Println(majorityElement1(s))
fmt.Println(majorityElement2(s))
fmt.Println(majorityElement3(s))
fmt.Println(majorityElement4(s))
}
15.反转链表(206)
给一个单链表的头节点 head ,请你反转链表,并返回反转后的链表
例如:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
输入:head = []
输出:[]
type ListNode struct {
Val int
Next *ListNode
}
func reverseList1(head *ListNode) *ListNode {
var nPrev *ListNode
nNow := head
for nNow != nil {
tempNode := nNow.Next
nNow.Next = nPrev
nPrev = nNow
nNow = tempNode
}
return nPrev
}
func reverseList2(head *ListNode) *ListNode {
if head == nil || head.Next == nil {
return head
}
newHead := reverseList2(head.Next)
head.Next.Next = head
head.Next = nil
return newHead
}
func main() {
node1 := new(ListNode)
node2 := new(ListNode)
node3 := new(ListNode)
node4 := new(ListNode)
node5 := new(ListNode)
node1.Val = 1
node1.Next = node2
node2.Val = 2
node2.Next = node3
node3.Val = 3
node3.Next = node4
node4.Val = 4
node4.Next = node5
node5.Val = 5
b := reverseList1(node1)
for b != nil {
fmt.Println(b.Val)
b = b.Next
}
}
16.翻转二叉树(226)
给一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点
例如:
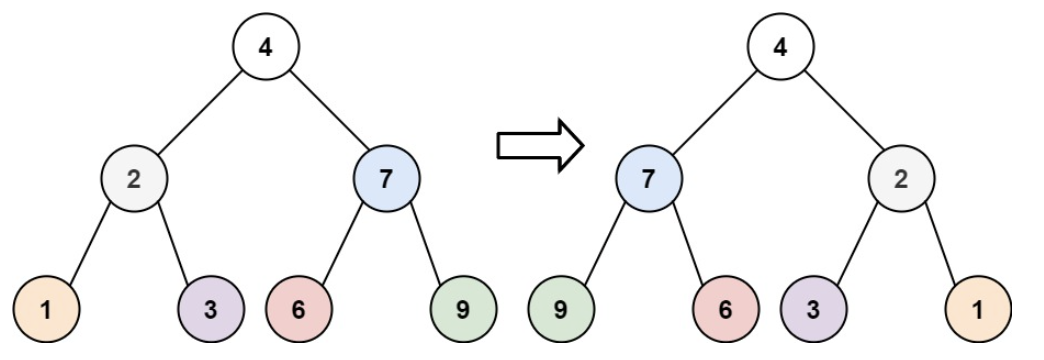
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
输入:root = []
输出:[]
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func invertTree1(root *TreeNode) *TreeNode {
if root == nil {
return nil
}
var queue []*TreeNode
queue = append(queue, root)
for len(queue) > 0 {
tempA := queue[0]
queue = queue[1:]
tempData := tempA.Left
tempA.Left = tempA.Right
tempA.Right = tempData
if tempA.Left != nil {
queue = append(queue, tempA.Left)
}
if tempA.Right != nil {
queue = append(queue, tempA.Right)
}
}
return root
}
func invertTree2(root *TreeNode) *TreeNode {
if root == nil {
return nil
}
left := invertTree2(root.Left)
right := invertTree2(root.Right)
root.Left = right
root.Right = left
return root
}
func main() {
}
17.回文链表(234)
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true,否则,返回 false
能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题
示例1:
输入:head = [1,2,2,1]
输出:true
输入:head = [1,2]
输出:false
type ListNode struct {
Val int
Next *ListNode
}
func isPalindrome1(head *ListNode) bool {
var reverseList func(head *ListNode) *ListNode
reverseList = func(head *ListNode) *ListNode {
var prev, cur *ListNode = nil, head
for cur != nil {
nextTmp := cur.Next
cur.Next = prev
prev = cur
cur = nextTmp
}
return prev
}
var endOfFirstHalf func(head *ListNode) *ListNode
endOfFirstHalf = func(head *ListNode) *ListNode {
fast := head
slow := head
for fast.Next != nil && fast.Next.Next != nil {
fast = fast.Next.Next
slow = slow.Next
}
return slow
}
if head == nil {
return true
}
firstHalfEnd := endOfFirstHalf(head)
secondHalfStart := reverseList(firstHalfEnd.Next)
p1 := head
p2 := secondHalfStart
result := true
for result && p2 != nil {
if p1.Val != p2.Val {
result = false
}
p1 = p1.Next
p2 = p2.Next
}
firstHalfEnd.Next = reverseList(secondHalfStart)
return result
}
func isPalindrome2(head *ListNode) bool {
var vals []int
for ; head != nil; head = head.Next {
vals = append(vals, head.Val)
}
n := len(vals)
for i, v := range vals[:n/2] {
if v != vals[n-1-i] {
return false
}
}
return true
}
func main() {
node1 := new(ListNode)
node2 := new(ListNode)
node3 := new(ListNode)
node4 := new(ListNode)
node1.Val = 1
node1.Next = node2
node2.Val = 2
node2.Next = node3
node3.Val = 2
node3.Next = node4
node4.Val = 1
fmt.Println(isPalindrome1(node1))
fmt.Println(isPalindrome2(node1))
}
18.移动零(283)
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
func moveZeroes1(nums []int) {
length := len(nums)
if length == 0 || length == 1 {
return
}
prev, cur := 0, 1
for cur < length && prev != cur {
for nums[prev] != 0 && prev < cur {
prev++
}
if nums[prev] == 0 && nums[cur] == 0 {
cur++
}
if cur < length && nums[prev] == 0 && nums[cur] != 0 {
tempData := nums[prev]
nums[prev] = nums[cur]
nums[cur] = tempData
prev++
cur++
} else {
cur++
}
}
}
func moveZeroes2(nums []int) {
left, right, n := 0, 0, len(nums)
for right < n {
if nums[right] != 0 {
nums[left], nums[right] = nums[right], nums[left]
left++
}
right++
}
}
func main() {
nums := []int{0, 1, 0, 3, 12}
moveZeroes1(nums)
fmt.Println(nums)
}
19.比特位计数(338)
给你一个整数 n ,对于0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,
返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
func countBits1(n int) []int {
var onesCount func(x int) int
onesCount = func(x int) (ones int) {
for ; x > 0; x &= x - 1 {
ones++
}
return
}
bits := make([]int, n+1)
for i := range bits {
bits[i] = onesCount(i)
}
return bits
}
func countBits2(n int) []int {
bits := make([]int, n+1)
highBit := 0
for i := 1; i <= n; i++ {
if i&(i-1) == 0 {
highBit = i
}
bits[i] = bits[i-highBit] + 1
}
return bits
}
func countBits3(n int) []int {
bits := make([]int, n+1)
for i := 1; i <= n; i++ {
bits[i] = bits[i>>1] + i&1
}
return bits
}
func countBits4(n int) []int {
bits := make([]int, n+1)
for i := 1; i <= n; i++ {
bits[i] = bits[i&(i-1)] + 1
}
return bits
}
func main() {
n := 10
fmt.Println(countBits1(n))
fmt.Println(countBits2(n))
fmt.Println(countBits3(n))
fmt.Println(countBits4(n))
}
20.找到所有数组中消失的数字(448)
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。
请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗?
示例 1:
输入:nums = [4,3,2,7,8,2,3,1]
输出:[5,6]
示例 2:
输入:nums = [1,1]
输出:[2]
func findDisappearedNumbers(nums []int) []int {
n := len(nums)
for _, v := range nums {
v = (v - 1) % n
nums[v] += n
}
var ans []int
for i, v := range nums {
if v <= n {
ans = append(ans, i+1)
}
}
return ans
}
func main() {
nums := []int{4, 3, 2, 7, 8, 2, 3, 1}
fmt.Println(findDisappearedNumbers(nums))
}
21.汉明距离(461)
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4
输出:2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
示例 2:
输入:x = 3, y = 1
输出:1
func hammingDistance1(x int, y int) int {
return bits.OnesCount(uint(x ^ y))
}
func hammingDistance2(x int, y int) int {
var ans int
for s := x ^ y; s > 0; s >>= 1 {
ans += s & 1
}
return ans
}
func hammingDistance3(x int, y int) int {
var ans int
for s := x ^ y; s > 0; s &= s - 1 {
ans++
}
return ans
}
func main() {
x := 1
y := 4
fmt.Println(hammingDistance1(x, y))
fmt.Println(hammingDistance2(x, y))
fmt.Println(hammingDistance3(x, y))
}
22.二叉树的直径(543)
给定一棵二叉树,你需要计算它的直径长度。
一棵二叉树的直径长度是任意两个结点路径长度中的最大值。
这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回3, 它的长度是路径 [4,2,1,3] 或者[5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func max(a, b int) int {
if a < b {
return b
}
return a
}
func diameterOfBinaryTree(root *TreeNode) int {
var ans = 1
var depth func(root *TreeNode) int
depth = func(root *TreeNode) int {
if root == nil {
return 0
}
l := depth(root.Left)
r := depth(root.Right)
ans = max(l+r+1, ans)
return max(l, r) + 1
}
depth(root)
return ans - 1
}
23.合并二叉树(217)
给两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会),
你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,
那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
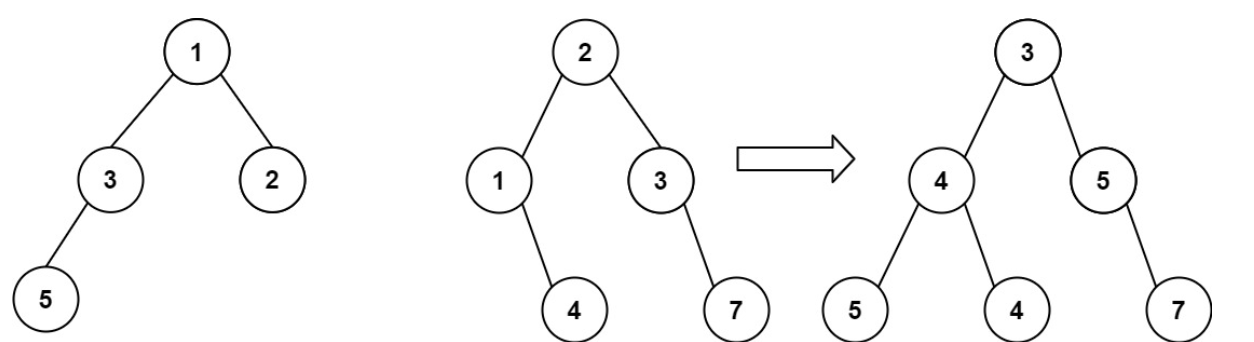
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2]
输出:[2,2]
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func mergeTrees1(root1 *TreeNode, root2 *TreeNode) *TreeNode {
if root1 == nil {
return root2
}
if root2 == nil {
return root1
}
root1.Val += root2.Val
root1.Left = mergeTrees1(root1.Left, root2.Left)
root2.Right = mergeTrees1(root1.Right, root2.Right)
return root1
}
func mergeTrees2(root1 *TreeNode, root2 *TreeNode) *TreeNode {
if root1 == nil {
return root2
}
if root2 == nil {
return root1
}
merged := &TreeNode{Val: root1.Val + root2.Val}
queue := []*TreeNode{merged}
queue1 := []*TreeNode{root1}
queue2 := []*TreeNode{root2}
for len(queue1) > 0 && len(queue2) > 0 {
node := queue[0]
queue = queue[1:]
node1 := queue1[0]
queue1 = queue1[1:]
node2 := queue2[0]
queue2 = queue2[1:]
left1, right1 := node1.Left, node1.Right
left2, right2 := node2.Left, node2.Right
if left1 != nil || left2 != nil {
if left1 != nil && left2 != nil {
left := &TreeNode{Val: left1.Val + left2.Val}
node.Left = left
queue = append(queue, left)
queue1 = append(queue1, left1)
queue2 = append(queue2, left2)
} else if left1 != nil {
node.Left = left1
} else {
node.Left = left2
}
}
if right1 != nil || right2 != nil {
if right1 != nil && right2 != nil {
right := &TreeNode{Val: right1.Val + right2.Val}
node.Right = right
queue = append(queue, right)
queue1 = append(queue1, right1)
queue2 = append(queue2, right2)
} else if right1 != nil {
node.Right = right1
} else {
node.Right = right2
}
}
}
return merged
}
func main() {
}
|




