背景

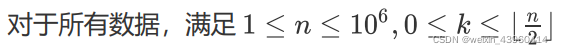
在这里插入图片描述

题面

在这里插入图片描述

题解

初步转换，我们得把序列前面的 1 同后面的 2 配对，最大化配对数。

然后，我们可以通过调整法，使得最优方案配对连线不交叉。在不交叉的条件下，我们可以找到一种贪心构造方案，就是从左到右进行“括号匹配”，把 1 当左括号，2 当右括号。若右括号失配则直接丢弃，左括号最终失配也丢弃，成功匹配的括号对数就是答案。

接下来我们不妨先考虑只有右括号失配的方案数。

$k$ 直接提供了失配右括号的总数 $x$ ，我们把左括号看作 $+ 1$ ，右括号看作 $? 1$ ，最终的序列总和就是 $? x$ 。由此，还可以得到一个必要条件：每一个前缀都不小于 $? x$ 。

不难发现此必要条件也是充分条件：考虑前缀和在整数上是连续变化的，每出现一个失配右括号，前缀最小值都会 $? 1$ ，否则，前面一定可以找到一个与之匹配的左括号。

所以，只有右括号失配的方案数等于 总和为 $? x$ 、前缀和均 $\geq-x$ 的仅含 ${-1,1\}$ 序列个数。

应用卡塔兰数和组合数的结论，不难得出表达式为 $C_n^{k}-C_n^{k-1}$ 。

我们再考虑存在左括号失配的情况。一个左括号失配等价于后缀和贡献最小值，但这样不好想。

我们其实可以将只有右括号失配的情况调整为所有情况。要把一个失配右括号变成失配左括号，前提条件是右边的失配右括号全部变成了失配左括号。

也就是说，我们只有 $x + 1$ 种调整方案（包括不动），乘上去就好了。

综上，
$way_k=(C_n^{k}-C_n^{k-1})\cdot (n-2k+1)$

硬算 $O (n)$ 。

CODE

#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#pragma GCC optimize(2)
using namespace std;
#define MAXN 1000005
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
int xchar() {
	static const int maxn = 1000000;
	static char b[maxn];
	static int pos = 0,len = 0;
	if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
	if(pos == len) return -1;
	return b[pos ++];
}
// #define getchar() xchar()
LL read() {
	LL f = 1,x = 0;int s = getchar();
	while(s < '0' || s > '9') {if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
	while(s >= '0' && s <= '9') {x = (x<<1) + (x<<3) + (s^48);s = getchar();}
	return f*x;
}
void putpos(LL x) {if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
	if(!x) {putchar('0');return ;}
	if(x<0) putchar('-'),x = -x;
	return putpos(x);
}
void AIput(LL x,int c) {putnum(x);putchar(c);}

const int MOD = 998244353;
int n,m,s,o,k;
int fac[MAXN],inv[MAXN],invf[MAXN];
int C(int n,int m) {
	if(m < 0 || m > n) return 0;
	return fac[n] *1ll* invf[n-m] % MOD * invf[m] % MOD;
}
int f(int k) {
	int x = n - k*2;
	return (C(n,k) +MOD- C(n,k-1)) %MOD *1ll* (x+1) % MOD;
}
int main() {
	freopen("merchant.in","r",stdin);
	freopen("merchant.out","w",stdout);
	int tp = read();
	n = read();
	fac[0]=fac[1]=inv[0]=inv[1]=invf[0]=invf[1]=1;
	for(int i = 2;i <= n;i ++) {
		fac[i] = fac[i-1] *1ll* i % MOD;
		inv[i] = (MOD - inv[MOD%i]) *1ll* (MOD/i) % MOD;
		invf[i] = invf[i-1] *1ll* inv[i] % MOD;
	}
	if(tp == 1) {
		k = read();
		return AIput(f(k),'\n'),0;
	}
	int ans = 0;
	for(int i = 0,pw = 1;(i<<1) <= n;i ++,pw = pw*233ll%MOD) {
		(ans += f(i) *1ll* pw % MOD) %= MOD;
	}
	AIput(ans,'\n');
	return 0;
}