00 写在前面
二叉树的遍历分为两种,递归和迭代。
递归是不好想但是实现简单的那种,迭代则是符合思考模式却不好实现的那种。
这次总结一下递归,迭代和统一迭代三种方法。
01 二叉树遍历
首先需要知道的是二叉树的遍历顺序,包括前序、中序和后序。这三种遍历的区别在于根节点的位置。
前序遍历是中左右,中序遍历是左中右,后续遍历是左右中。
另外还需要复习一下二叉树节点的结构:
struct TreeNode{
int val;
TreeNode *left;
TreeNode *right;
};
和链表差不多。
02 二叉树递归遍历
递归需要特别注意三个点:
- 函数的参数和返回值
- 递归终止的条件
- 每层的逻辑
前序遍历
先构造函数,输出遍历后的节点,不需要返回值
void PreOrder(TreeNode* cur,vector<int> &vec){
if(cur==NULL)return;
vec.push_back(cur->val);//中节点
PreOrder(cur->left,vec);//左孩子
PreOrder(cur->right,vec);//右孩子
}
首先把中节点存入,再递归遍历左孩子和右孩子。形成中左右的顺序。
这里不使用vector存也可以,直接输出。
中序遍历
中序遍历只需要修改一下遍历顺序即可。形成左中右的顺序。
void InOrder(TreeNode* cur,vector<int> &vec){
if(cur==NULL)return;
PreOrder(cur->left,vec);//左孩子
vec.push_back(cur->val);//中节点
PreOrder(cur->right,vec);//右孩子
}
后序遍历
后序遍历也只需要修改一下遍历顺序即可。形成左右中的顺序。
void PostOrder(TreeNode* cur,vector<int> &vec){
if(cur==NULL)return;
PreOrder(cur->left,vec);//左孩子
PreOrder(cur->right,vec);//右孩子
vec.push_back(cur->val);//中节点
}
03 二叉树的迭代遍历
递归遍历很好实现,只需要改动遍历顺序,而迭代实现起来就要复杂一些了。
迭代法实现的具体做法是使用栈来完成遍历操作。
我们可以在遍历时把节点存入,再按照想要遍历的顺序弹出。
前序遍历
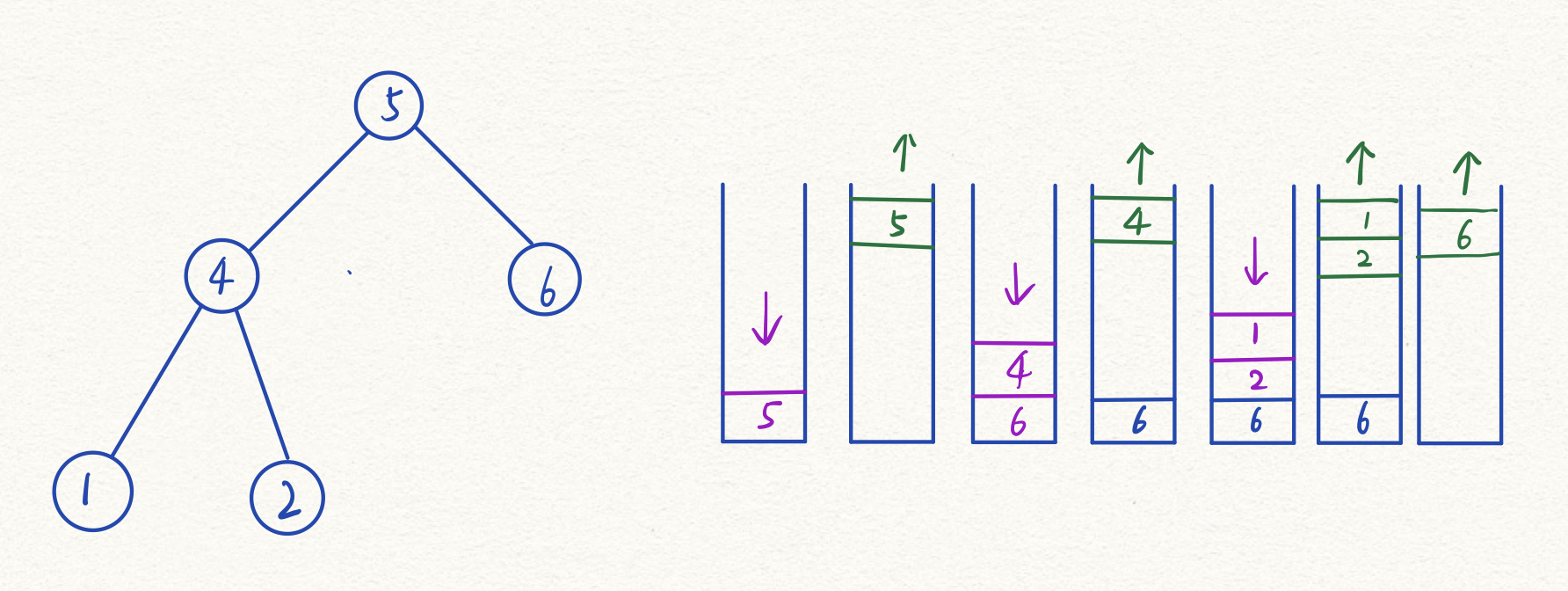
前序遍历是中左右的顺序,因为要使用栈,所以进栈时应该是右左。
先将当前节点入栈,然后弹出,再将它的右子树和左子树入栈,弹出左子树,再将其右子树和左子树入栈…最后按顺序弹出。
vector<int> PreOrder(TreeNode *root){
stack<TreeNode*>st;//遍历栈
vector<int>result;//用于存放结果的vector
if(root==NULL)return result;
st.push(root);//先把根入栈
while(!st.empty()){
TreeNode *node=st.top();//中节点,记录后弹出,再找左右子树
st.pop();
result.push_back(node->val);
if(node->right)st.push(node->right);//先入右子树,这样右子树后出。
if(node->left)st.push(node->left);//后入左子树,这样左子树先出。
}
}
中序遍历
中序遍历有一个不同的点,导致它不可以通过前序遍历改改顺序来实现。
我们仔细想想,中序遍历的顺序是左中右,这意味着我们一开始就要到达最左下角并将其弹出,而这时如果使用栈就会无法实现。
所以中序遍历需要额外的指针来进行遍历,栈只负责处理节点。
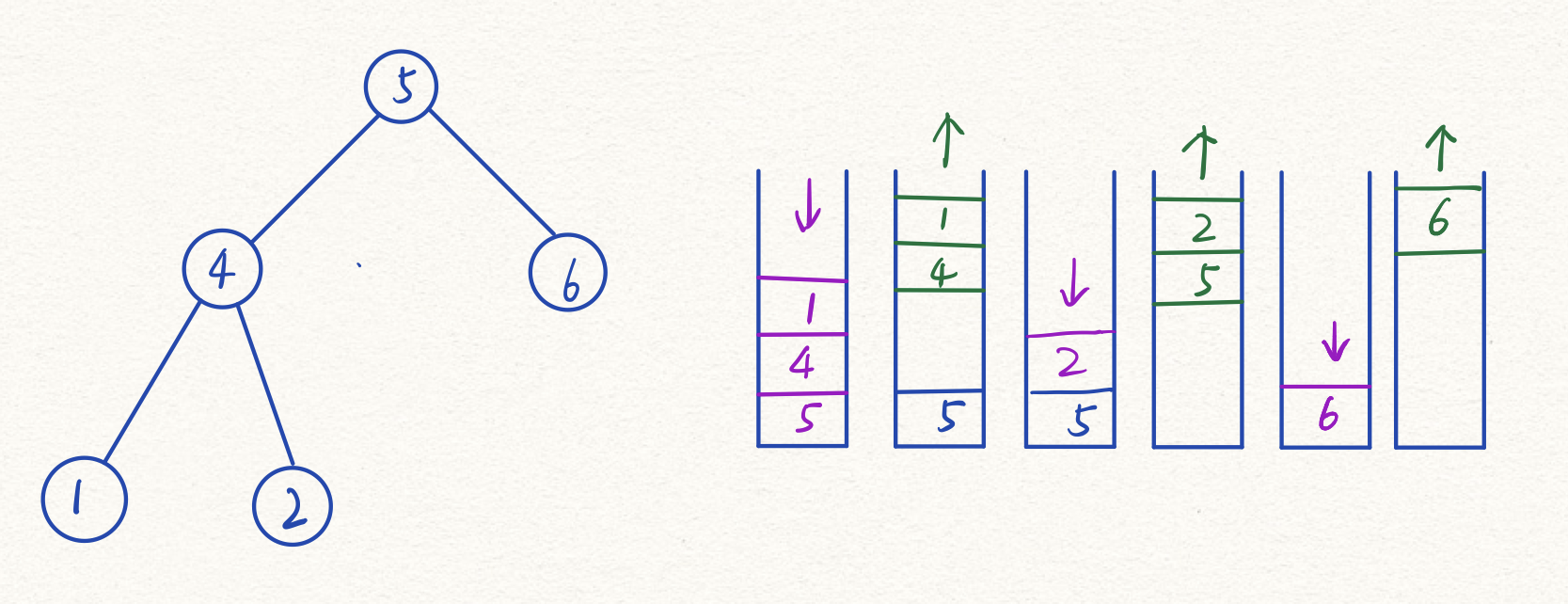
vector<int> InOrder(TreeNode *root){
stack<TreeNode*>st;//遍历栈
vector<int>result;//用于存放结果的vector
TreeNode *cur=root;//遍历指针,先指向根
while(cur!=NULL||!st.empty()){
if(cur!=NULL){//先要走到最底层,将沿途节点存入栈
st.push(cur);
cur=cur->left;
}
else{//到达底层,开始弹出,并且将右子树入栈,如果没有就返回上一层父节点,因为父节点已经入栈了。
cur=st.top();
st.pop();
result.push_back(cur->val);
cur=cur->right;
}
}
return result;
}
这里使用cur是否为空来进行分支判断的设计比较巧妙。
后序遍历
后序遍历的顺序是左右中,如果想要优化结构不使用cur,可以这样实现:先实现先序遍历的中左右顺序,我们可以再调整为中右左,最后将数组反转就可以得到左右中的顺序了。
vector<int> PostOrder(TreeNode *root){
stack<TreeNode*>st;//遍历栈
vector<int>result;//用于存放结果的vector
if(root==NULL)return result;
st.push(root);
while(!st.empty()){
TreeNode * node=st.top();
st.pop();
result.push_back(node->val);
if(node->left)st.push(node->left);//要想实现先右后左,进栈时需要先左后右。
if(node->right)st.push(node->right);
}
reverse(result.begin(),result.end());
return result;
}
04 二叉树的统一迭代
从上面的迭代遍历我们可以看出,迭代并不能像递归一样修改遍历顺序实现。
但是还是有一种方法可以统一二叉树迭代的写法的,那就是使用空指针。
中序遍历
看一个中序遍历的例子,正确顺序为14256
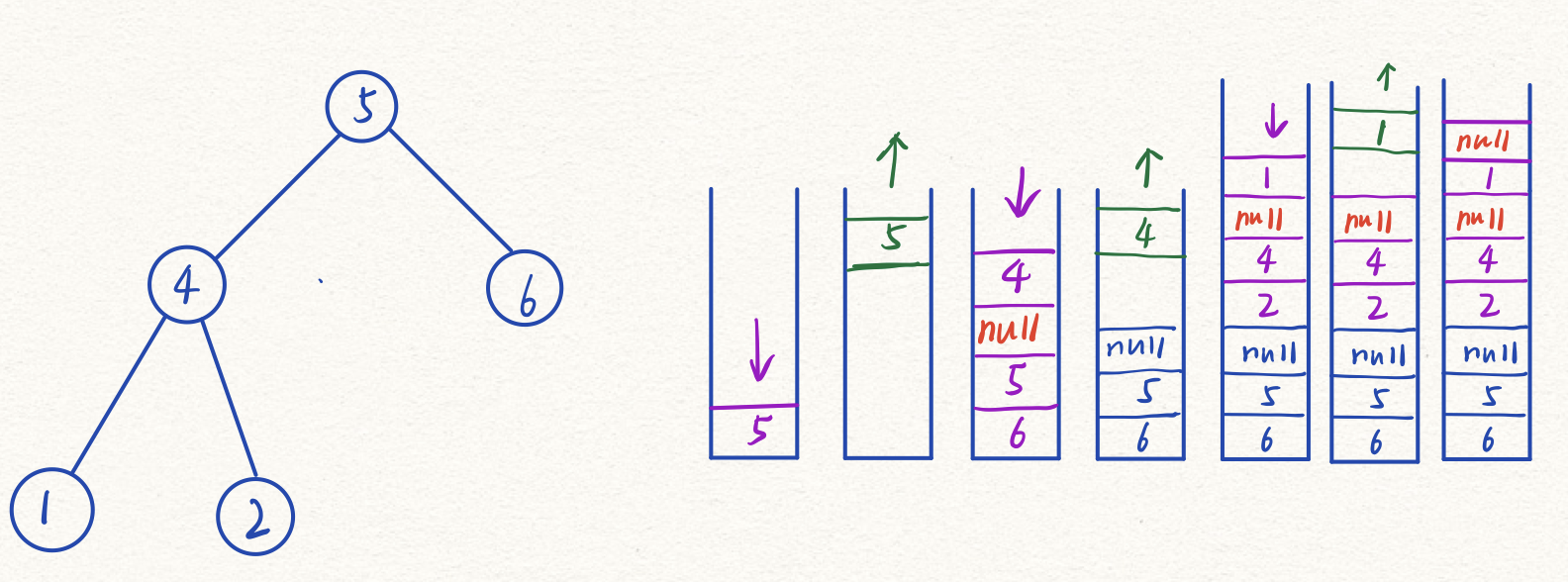
先把根节点入栈,然后在遍历中先弹出目前节点,再按照右中左的顺序入栈(因为中序是左中右)
这里的null是在中节点添加后入栈的,代表此时中节点已经被访问但是没有进行处理。
按此顺序处理后我们可以看到此时栈里面的顺序就是最后的结果了,当然到这里还没有结束。
遇到空节点时,取出非空的栈顶元素,然后计入结果。
vector<int> InOrder(TreeNode * root){
vector<int>result;
stack<TreeNode*>st;
if(root==NULL)return result;
st.push(root);//根节点入栈
while(!st.empty()){
TreeNode *node=st.top();
if(node!=NULL){
st.pop();//先弹出防止重复操作
if(node->right)
st.push(node->right);//右孩子入栈
st.push(node);//中节点入栈
st.push(NULL);//添加null标记
if(node->left)
st.push(node->left);//左孩子入栈
}
else{//遇到空节点的操作
st.pop();//首先把空节点弹出
node=st.top();//取正确的栈顶
st.pop();
result.push_back(node->val);
}
}
return result;
}
用这种方法就可以统一前序中序和后序遍历了。
前序遍历
前序遍历是中左右,按照入栈顺序为右左中。
vector<int> InOrder(TreeNode * root){
vector<int>result;
stack<TreeNode*>st;
if(root==NULL)return result;
st.push(root);//根节点入栈
while(!st.empty()){
TreeNode *node=st.top();
if(node!=NULL){
st.pop();//先弹出防止重复操作
if(node->right)
st.push(node->right);//右孩子入栈
if(node->left)
st.push(node->left);//左孩子入栈
st.push(node);//中节点入栈
st.push(NULL);//添加null标记
}
else{//遇到空节点的操作
st.pop();//首先把空节点弹出
node=st.top();//取正确的栈顶
st.pop();
result.push_back(node->val);
}
}
return result;
}
后序遍历
后序遍历是左右中,按照入栈顺序为中右左。
vector<int> InOrder(TreeNode * root){
vector<int>result;
stack<TreeNode*>st;
if(root==NULL)return result;
st.push(root);//根节点入栈
while(!st.empty()){
TreeNode *node=st.top();
if(node!=NULL){
st.pop();//先弹出防止重复操作
st.push(node);//中节点入栈
st.push(NULL);//添加null标记
if(node->right)
st.push(node->right);//右孩子入栈
if(node->left)
st.push(node->left);//左孩子入栈
}
else{//遇到空节点的操作
st.pop();//首先把空节点弹出
node=st.top();//取正确的栈顶
st.pop();
result.push_back(node->val);
}
}
return result;
}
if(node->left)
st.push(node->left);//左孩子入栈
}
else{//遇到空节点的操作
st.pop();//首先把空节点弹出
node=st.top();//取正确的栈顶
st.pop();
result.push_back(node->val);
}
}
return result;
}
