[数据结构与算法]数据结构之并查集

1. 并查集（Union Find）

也叫做不相交集合（Disjoint Set）

• 核心操作：

1. 查找（Find）：查找元素所在的集合；
2. 合并（Union）：将两个元素所在的集合合并为一个集合；

1.1 存储方式

假设并查集处理的数据都是整性，可以使用整性数组来存储数据。

• 存储结构
  
• 逻辑结构
  

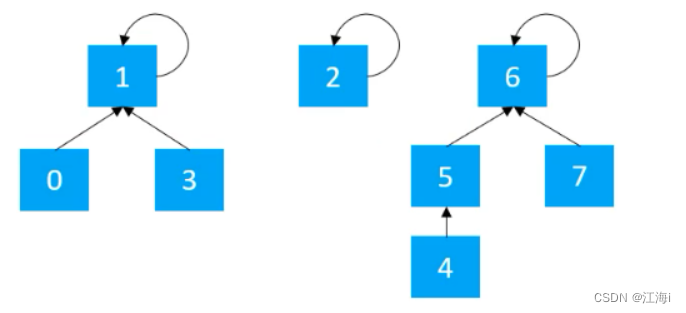
可以看出：（0、1、3）是一个集合；（4、5、6、7）是一个集合；2自己一个集合。

1.2 抽象类设计

/**
 * @Description UnionFind 抽象类
 * @date 2022/5/9 20:28
 */
public abstract class AbstractUnionFind {

    protected int[] parents;

    public AbstractUnionFind(int capacity) {
        // 判断容量是否符合要求
        if (capacity < 0){
            throw new IllegalArgumentException("Capacity must >= 1");
        }
        // 创建基于容量大小的数组
        parents = new int[capacity];

        // 指向自己 让自己作为一个单独的集合
        for (int i = 0; i < parents.length; i++) {
            parents[i] = i;
        }
    }

    /**
     * 检测索引是否合法
     * @param index
     */
    protected void rangeCheck(int index){
        if (index >= parents.length || index < 0){
            throw new IndexOutOfBoundsException("Index must less than array's length ");
        }
    }

    /**
     * 查找 v 的 所属集合（根节点）
     * @param v
     * @return
     */
    public abstract int find(int v);

    /**
     * 合并 v1 v2 的所属集合
     * @param v1
     * @param v2
     */
    public abstract void union(int v1, int v2);

     /**
     * 判断 v1 v2 是否属于同一个集合
     * @param v1
     * @param v2
     * @return
     */
    public boolean isSame(int v1, int v2){
        return find(v1) == find(v2);
    }
}

1.3 初始化

在执行初始化的时候，将值的父节点指向自己表示自己为一个单独的集合。

    private int[] parents;

    public QuickFind(int capacity) {
        // 判断容量是否符合要求
        if (capacity < 0){
            throw new IllegalArgumentException("Capacity must >= 1");
        }
        // 创建基于容量大小的数组
        parents = new int[capacity];

        // 指向自己 让自己作为一个单独的集合
        for (int i = 0; i < parents.length; i++) {
            parents[i] = i;
        }
    }

1.4 Quick Find方式实现并查集

1.4.1 union

union(v1, v2)将v1集合的所有元素都指向v2集合的根节点。

• 初始化之后：
• union(1, 0)：将1指向0的根节点。
  
• union(1,2)：将1所指向节点的所有原始的根节点都改为2的根节点
• 代码实现：

    @Override
    public void union(int v1, int v2) {
        // 获取两个值所在的集合（根节点值）
        int p1 = find(v1);
        int p2 = find(v2);
        // 如果根节点相同 就表示位于同一个集合中不需要合并
        if (p1 == p2) return;

        // 遍历数组中所有的元素，如果根节点与 v1 相同的都改为 v2 的根节点
        for (int i = 0; i < parents.length; i++) {
            if (parents[i] == p1){
                parents[i] = p2;
            }
        }
    }

1.4.2 find

直接返回数组中存储的根节点即可。

    /**
     * 检测索引是否合法
     * @param index
     */
    private void rangeCheck(int index){
        if (index >= parents.length || index < 0){
            throw new IndexOutOfBoundsException("Index must less than array's length ");
        }
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        // 因为这里直接指向的就是根节点，所以直接返回即可
        return parents[v];
    }

1.4.3 总结

1. union()的时间复杂度为O(n)；
2. find()的时间复杂度为O(1)。

1.5 QuickUnion

1.5.1 union

union(v1, v2)将v1集合的根节点都指向v2集合的根节点。

• 初始化之后：
• union(1, 0)：将1的根节点指向0的根节点：
  
• union(1,2)：将1的根节点指向2的根节点：
  
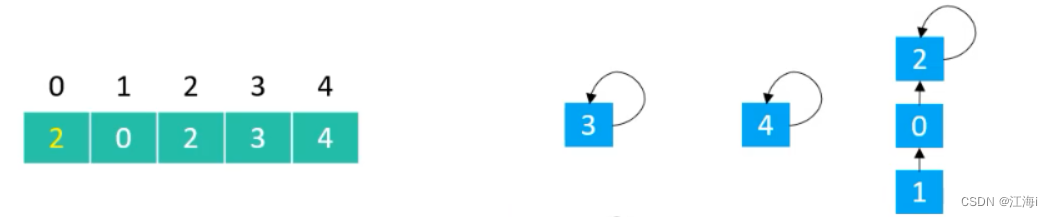
• union(4,1)：将4的根节点指向1的根节点：
  

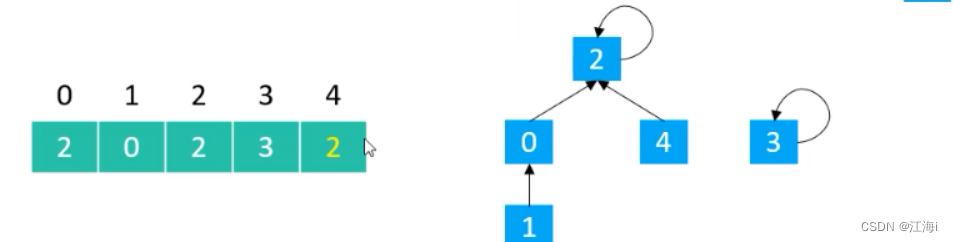
    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) return;
        // 将当前节点的父节点改为要修改的节点的父节点
        parents[p1] = p2;
    }

1.5.2 find

    @Override
    public int find(int v) {
        rangeCheck(v);
        // 一直往上找 知道当前元素的父节点是自己就表示为根节点
        while (v != parents[v]){
            v = parents[v];
        }
        return v;
    }

1.5.3 优化

在进行union()时，可以会出现树不平很的情况，甚至有可能会退化成链表。

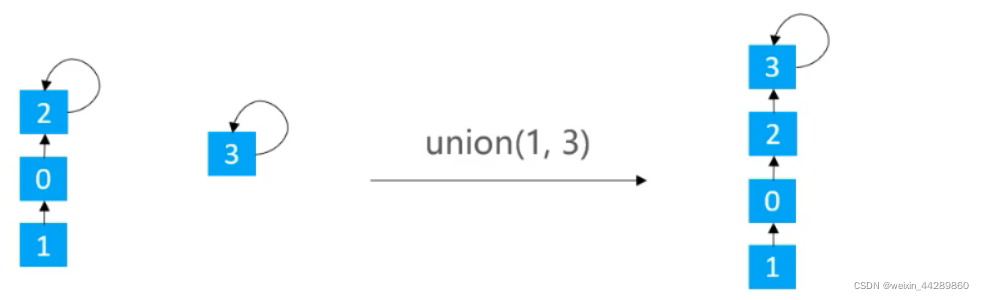
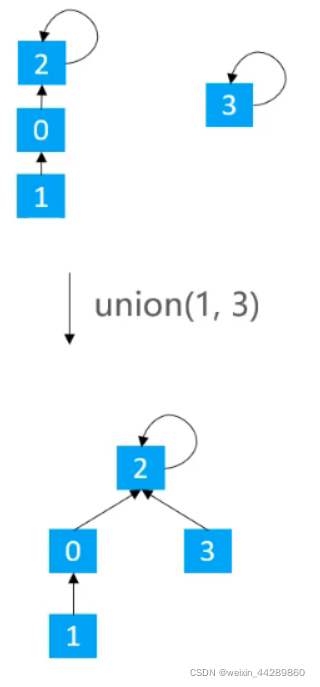
1.5.3.1 基于size的优化

元素少的树嫁接到元素多的树上。

/**
 * @Description QuickUnion size 优化版本
 * @date 2022/5/9 20:48
 */
public class QuickUnionSize extends AbstractUnionFind{

    // 记录当前元素的数量
    private int[] sizes;

    public QuickUnionSize(int capacity) {
        super(capacity);
        sizes = new int[capacity];
        // 将当前元素的数量默认为 1
        for (int i = 0; i < sizes.length; i++) {
            sizes[i] = 1;
        }
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        // 一直往上找 知道当前元素的父节点是自己就表示为根节点
        while (v != parents[v]){
            v = parents[v];
        }
        return v;
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) return;
        // 将数量少的嫁接到数量多的上面
        if (sizes[p1] < sizes[p2]){
            parents[p1] = p2;
            sizes[p2] += sizes[p1];
        }else {
            parents[p2] = p1;
            sizes[p1] += sizes[p2];
        }
    }
}

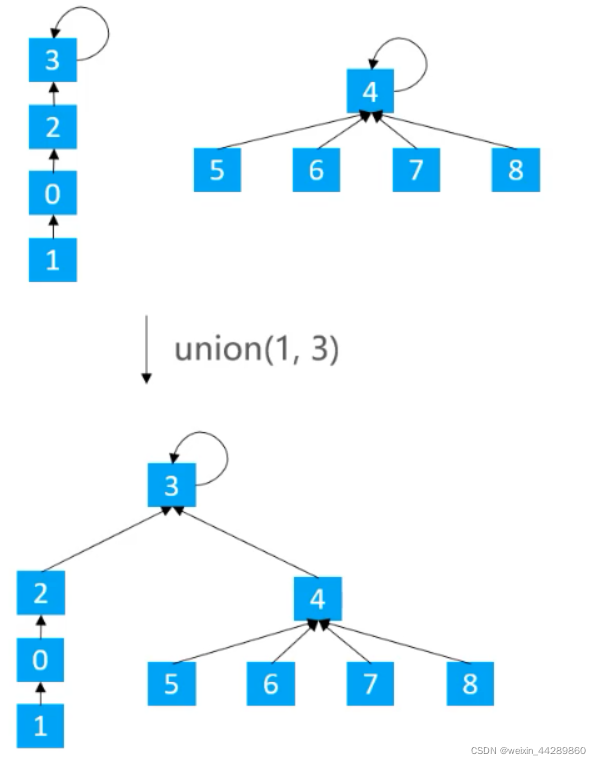
1.5.3.2 基于rank的优化

矮的树嫁接到高的树上。

/**
 * @Description QuickUnion rank 优化版本
 * @date 2022/5/9 20:48
 */
public class QuickUnionRank extends AbstractUnionFind{

    // 记录 '树' 的高度
    private int[] ranks;

    public QuickUnionRank(int capacity) {
        super(capacity);
        ranks = new int[capacity];
        // 将当前 ‘树’ 的高度默认为 1
        for (int i = 0; i < ranks.length; i++) {
            ranks[i] = 1;
        }
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        // 一直往上找 知道当前元素的父节点是自己就表示为根节点
        while (v != parents[v]){
            v = parents[v];
        }
        return v;
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) return;
        // 将矮的树嫁接到高的树上
        if (ranks[p1] < ranks[p2]){
            parents[p1] = p2;
        }else if (ranks[p1] > ranks[p2]){
            parents[p2] = p1;
        }else {
            parents[p1] = p2;
            ranks[p2] += 1;
        }
    }
}

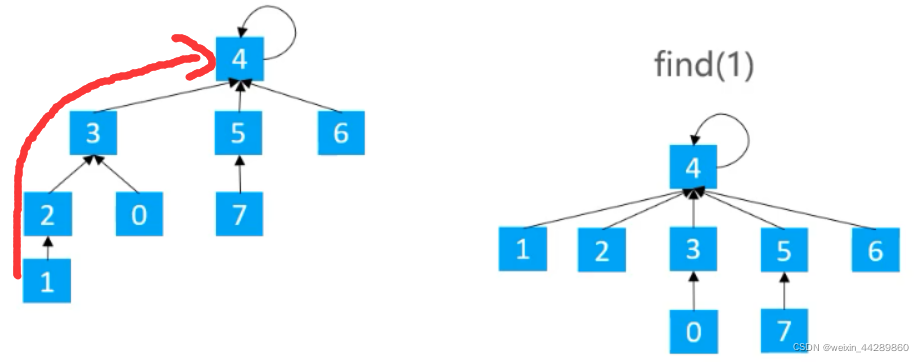
1.5.3.3 基于rank的优化 —— 路径压缩

在find()时，将路径上的所有节点都指向根节点，从而降低树的高度。

/**
 * @Description rank优化 —— 路径压缩
 * @date 2022/5/9 21:11
 */
public class QuickUnionPC extends AbstractUnionFind{
    // 记录 '树' 的高度
    private int[] ranks;

    public QuickUnionPC(int capacity) {
        super(capacity);
        ranks = new int[capacity];
        // 将当前 ‘树’ 的高度默认为 1
        for (int i = 0; i < ranks.length; i++) {
            ranks[i] = 1;
        }
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        // 递归调用 只要当前元素的父节点不是自己就一直往上并且赋值为根节点
        if (v != parents[v]){
            parents[v] = find(parents[v]);
        }
        return parents[v];
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) return;
        // 将矮的树嫁接到高的树上
        if (ranks[p1] < ranks[p2]){
            parents[p1] = p2;
        }else if (ranks[p1] > ranks[p2]){
            parents[p2] = p1;
        }else {
            parents[p1] = p2;
            ranks[p2] += 1;
        }
    }
}

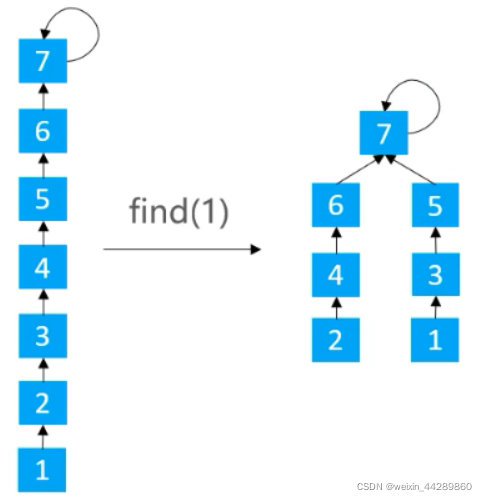
1.5.3.4 基于rank的优化 —— 路径分裂

find()时，使路径上的每个节点都指向其祖父节点。

/**
 * @Description rank优化 —— 路径减半
 * @date 2022/5/9 21:11
 */
public class QuickUnionPS extends AbstractUnionFind{
    // 记录 '树' 的高度
    private int[] ranks;

    public QuickUnionPS(int capacity) {
        super(capacity);
        ranks = new int[capacity];
        // 将当前 ‘树’ 的高度默认为 1
        for (int i = 0; i < ranks.length; i++) {
            ranks[i] = 1;
        }
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        // 让元素的父节点改为祖父节点
        while (v != parents[v]){
            int p = parents[v];
            parents[v] = parents[parents[v]];
            v = p;
        }
        return parents[v];
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) return;
        // 将矮的树嫁接到高的树上
        if (ranks[p1] < ranks[p2]){
            parents[p1] = p2;
        }else if (ranks[p1] > ranks[p2]){
            parents[p2] = p1;
        }else {
            parents[p1] = p2;
            ranks[p2] += 1;
        }
    }
}

1.5.3.5 基于rank的优化 —— 路径减半

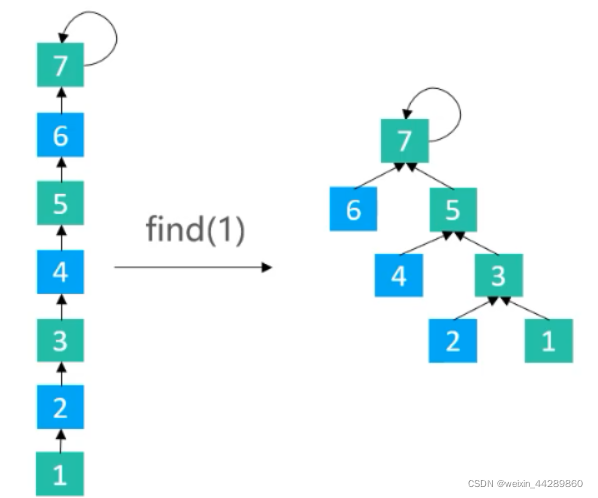
find()时，使路径上每隔一个节点就指向其祖父节点。

/**
 * @Description rank优化 —— 路径减半
 * @date 2022/5/9 21:11
 */
public class QuickUnionPV extends AbstractUnionFind{
    // 记录 '树' 的高度
    private int[] ranks;

    public QuickUnionPV(int capacity) {
        super(capacity);
        ranks = new int[capacity];
        // 将当前 ‘树’ 的高度默认为 1
        for (int i = 0; i < ranks.length; i++) {
            ranks[i] = 1;
        }
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        // 让元素的父节点改为祖父节点
        while (v != parents[v]){
            parents[v] = parents[parents[v]];
            v = parents[v];
        }
        return v;
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) return;
        // 将矮的树嫁接到高的树上
        if (ranks[p1] < ranks[p2]){
            parents[p1] = p2;
        }else if (ranks[p1] > ranks[p2]){
            parents[p2] = p1;
        }else {
            parents[p1] = p2;
            ranks[p2] += 1;
        }
    }
}

1.5.4 总结

• 优化之前的：

1. union()的时间复杂度为O(n)；
2. find()的时间复杂度为O(n)。

• 使用 rang或者size在添加以下三个中的一个路径分裂、路径减半、路径压缩之后：可以使两个操作的均摊时间复杂度优化为：O(α(n))其中α(n) < 5。
• 建议使用QuickUnion基于Rank优化再添加路径分裂或者路径减半。

1.6 自定义类型

1. 使用方法将自定义类型转为整型（比如生成哈希值，但要保证哈希值不相同）。
2. 链表 + map

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖