[数据结构与算法]算法 二叉树 AVL树

AVL树的定义

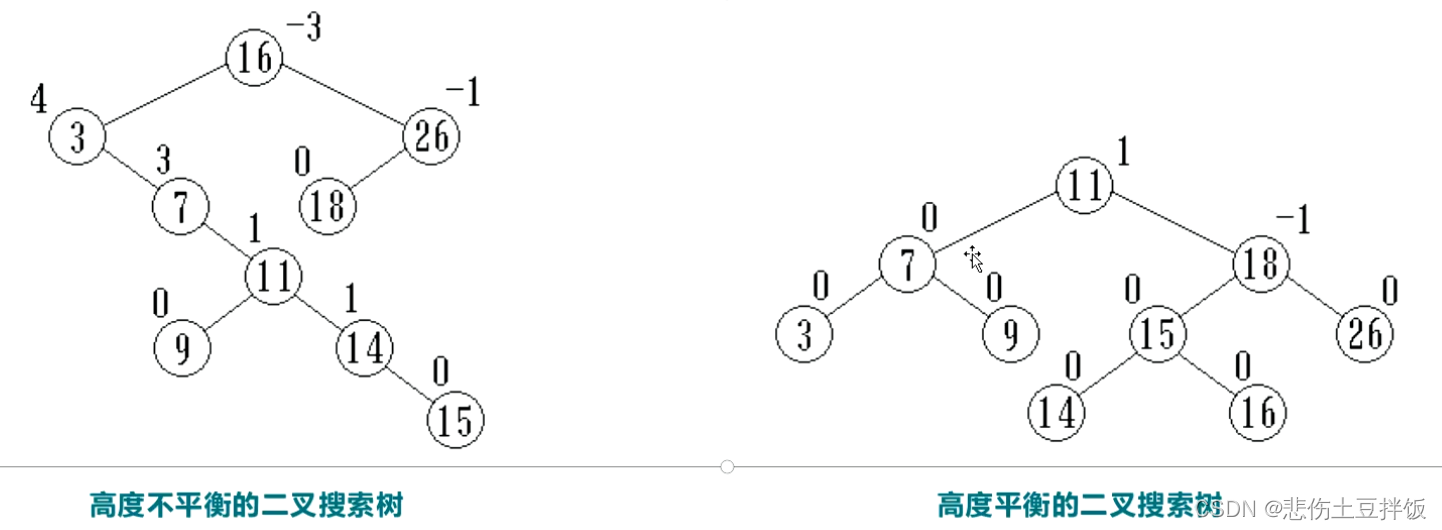
一颗AVL树或者是空树，或者是具有下列性质的二叉搜索树：它的左子树和右子树都是AVL树，且左子树和右子树的高度只差绝对值不超过 1

结点的平衡因子 balance

• 每个结点附加一个数字，给出该结点右子树的高度减去左子树的高度所得的高度差，这个数字即为结点的平衡因子balance
• 根据AVL 树的定义，任一结点的平衡因子只能取 -1、0 和 1
• 如果一个结点的平衡因子的绝对值大于1，则这颗二叉搜索树就失去了平衡，不再是AVL树
• 如果一棵二叉搜索树是高度平衡的，它就成为AVL树，如果它有 n 个结点，其高度可保持在O(log₂n)，平均搜索长度也可保持在O(log₂n)

AVL树的结构

typedef int KeyType;
typedef struct AVLNode
{
	KeyType key;
	struct AVLNode* leftchild;
	struct AVLNode* parent;
	struct AVLNode* rightchild;
	int balance;  //-1 0 1
}AVLNode, * AVLTree;

AVL树的插入

在向一颗本来是高度平衡（0，1，-1）的AVL树中插入一个新结点和在BST树一样，区别是，如果树中某个结点的平衡因子的绝对值 [balance] > 1，则出现了不平衡，需要做平衡化处理，使得树中各结点重新平衡化

平衡化旋转

• 如果在一棵平衡的二叉搜索树中插入一个新结点，造成了不平衡。此时必须调整树的结构，使之平衡化
• 平衡化旋转有两类：
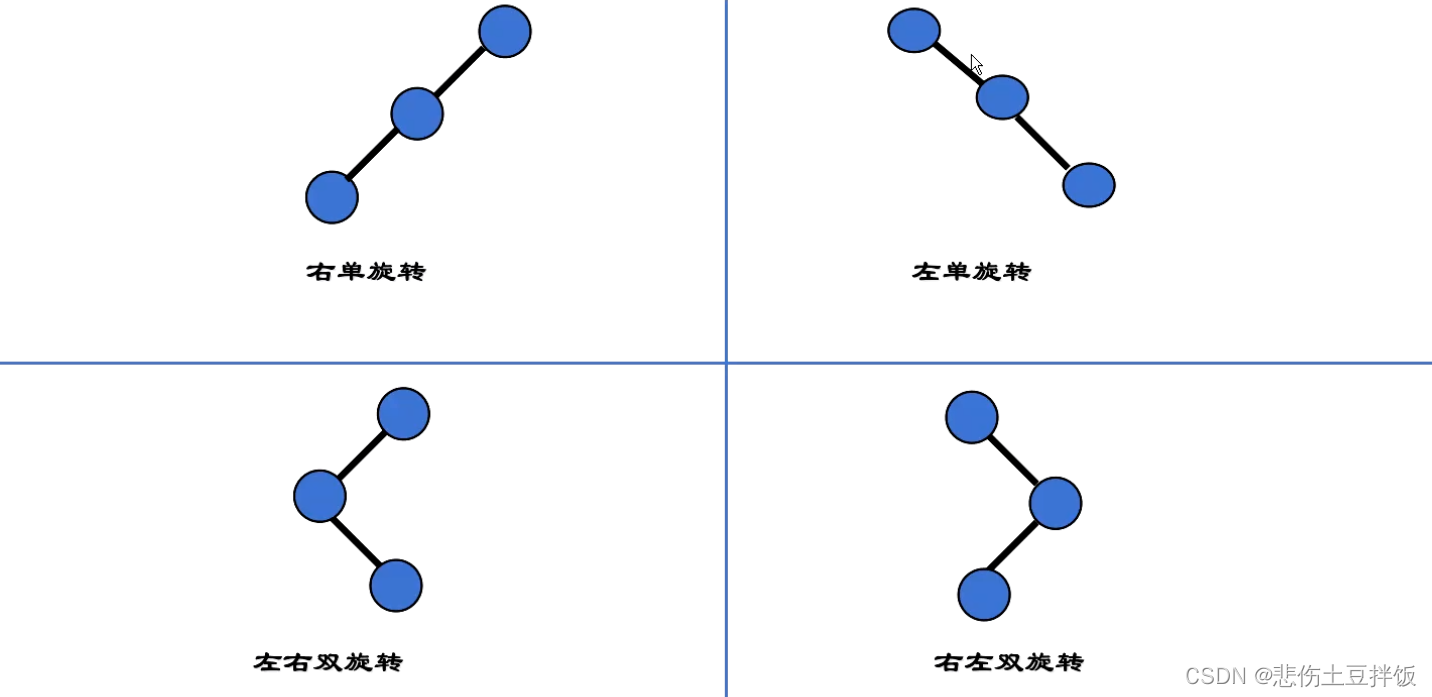
  1. 单旋转（左旋和右旋）
  2. 双旋转（左平衡和右平衡）
• 每插入一个新结点时，AVL树中相关结点的平衡状态会发生改变，因此，在插入一个新结点后，需要从插入位置沿通向根的路径回溯，检查各结点的平衡因子（左、右子树的高度差）
• 如果在某一结点发现高度不平衡，停止回溯
• 从发生不平衡的结点起，沿刚才回溯的路径取直接下两层的结点
• 如果在三个结点处于一条直线上，则采用单旋转进行平衡化，单旋转可按其方向分为左单旋转和右单旋转，其中一个是另一个的镜像，其方向与不平衡的形状相关
• 如果这三个结点处于一条折线上，则采用双旋转进行平衡化，双旋转分为先左后右和先右后左两类

左单旋转

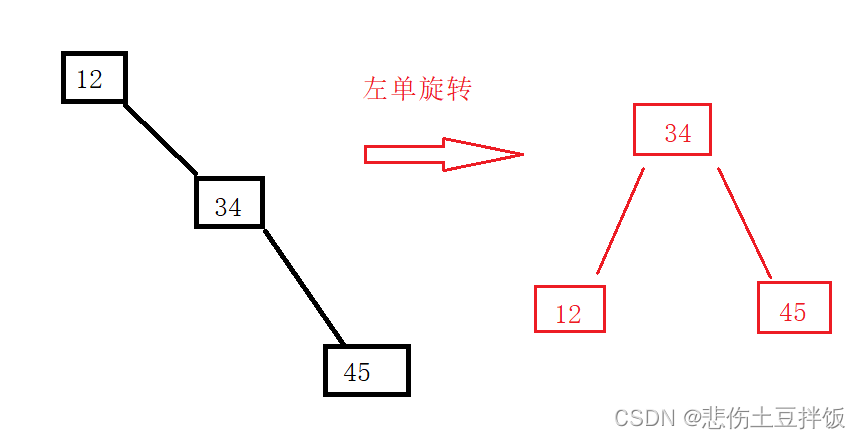
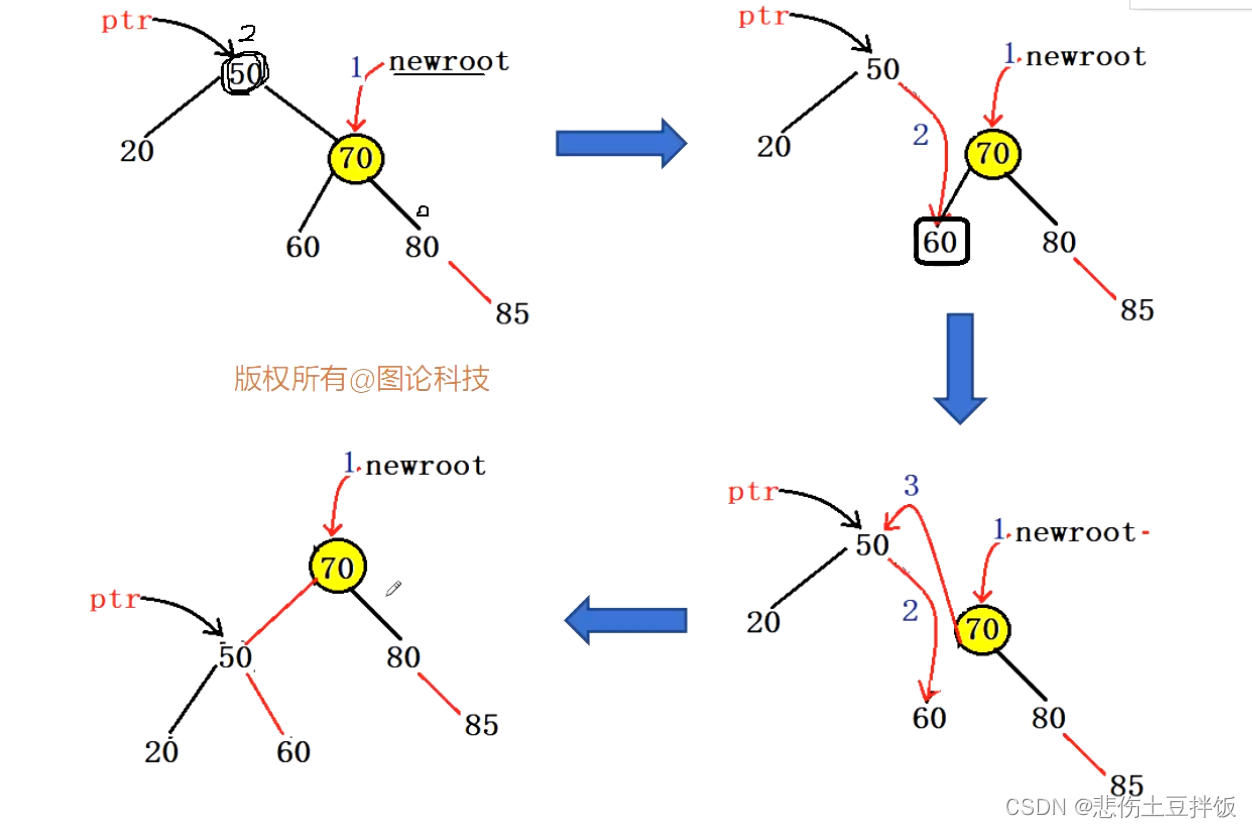
根据上图，当我们插入了结点85，70平衡因子变为1，50平衡因子变为2，失去平衡性；

• 那么将结点50作为ptr指针，将其进行旋转 ，使得ptr的右节点指向结点60，
• 令结点70的左子树指向结点50，继而规整成一个新的结点

void RotateLeft(AVLTree& tree, AVLNode* ptr)
{
	AVLNode* newroot = ptr->rightchild; //a
	newroot->parent = ptr->parent;   //1 切换父节点
	
	ptr->rightchild = newroot->leftchild;//b
	if (newroot->leftchild != nullptr)
	{
		newroot->leftchild->parent = ptr;//2
	}

	newroot->leftchild = ptr;   //c
	if (ptr == tree)
	{
		tree = newroot;
	}
	else
	{
		if (ptr->parent->leftchild == ptr)
		{
			ptr->parent->leftchild = newroot;
		}
		else
		{
			ptr->parent->rightchild = newroot;
		}
	}
	ptr->parent = newroot;  //3
}

这三句代码分别对应：
结点50右子树指向结点70左子树结点60，接着将结点70左子树指向结点50

右单旋转

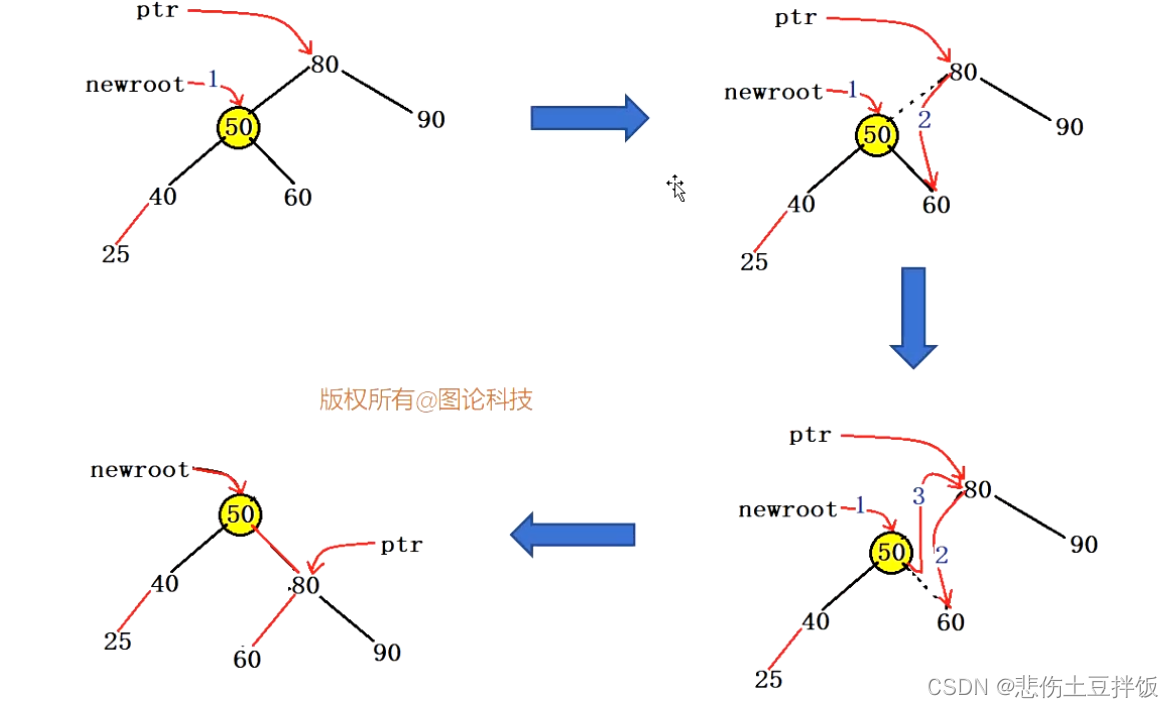
void RotateRight(AVLTree& tree, AVLNode* ptr)
{
	AVLNode* newroot = ptr->leftchild;
	newroot->parent = ptr->parent;

	if (newroot->rightchild  != nullptr)
	{
		newroot->rightchild->parent = ptr;
	}
	ptr->leftchild = newroot->rightchild;

	newroot->rightchild = ptr;
	if (ptr == tree)
	{
		tree = newroot;
	}
	else
	{
		if (ptr->parent->leftchild == ptr)
		{
			ptr->parent->leftchild = newroot;
		}
		else
		{
			ptr->parent->rightchild = newroot;
		}
	}

	ptr->parent = newroot;
}

与左单旋转类似，仅需要对其进行相对变形

左双旋转

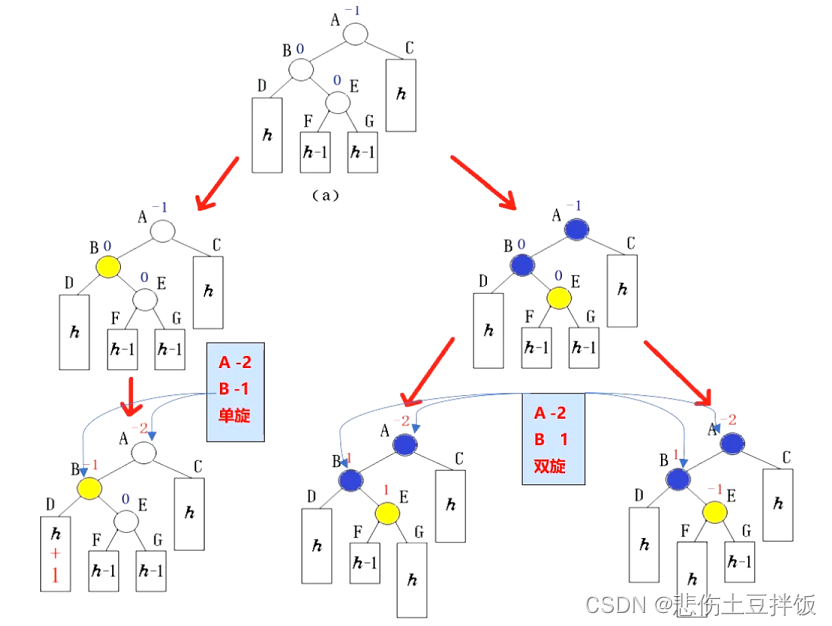
当我们在插入过程中，出现上面的情况，当我们新的结点插入F，或者G无论哪一个结点，出现了A->B->E 这样的一个折线，那么我们就需要进行双旋转进行二叉树的平衡

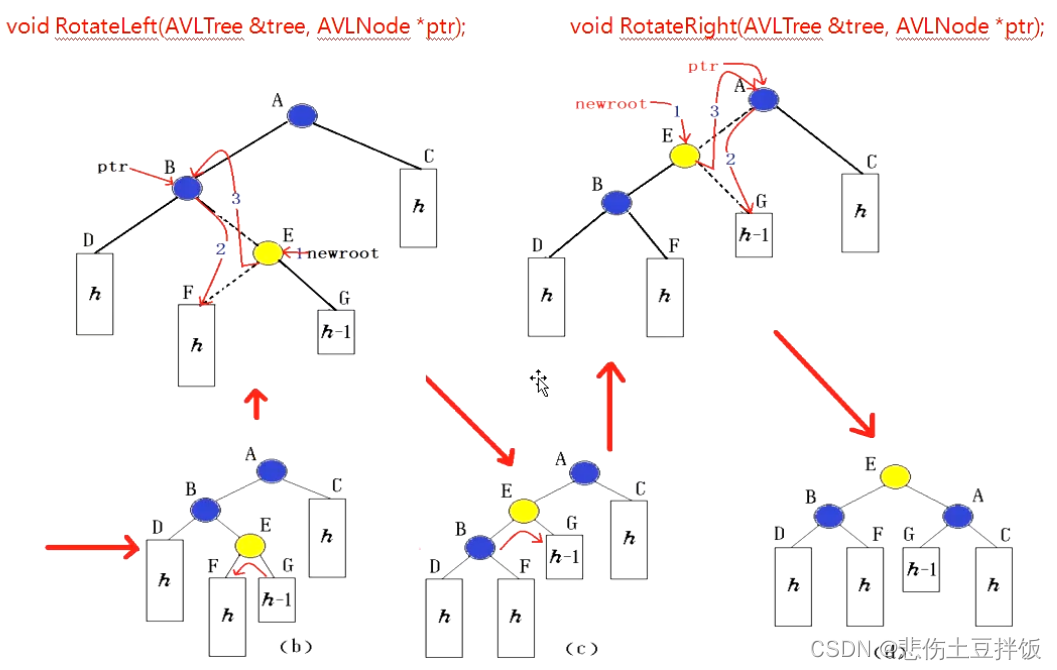
加入我们在F进行插入，E的平衡因子变为-1，B的平衡因子变为1，A的平衡因子变为-2，进行双旋转，首先以 B 作为 ptr 进行左单旋转，变为图(c ) 再将 A 作为 ptr E为旋转点进行右单旋转变为图(d)

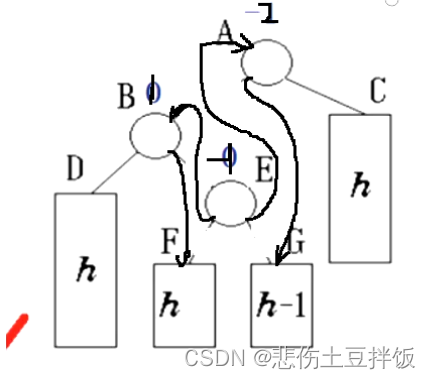
插入 insert

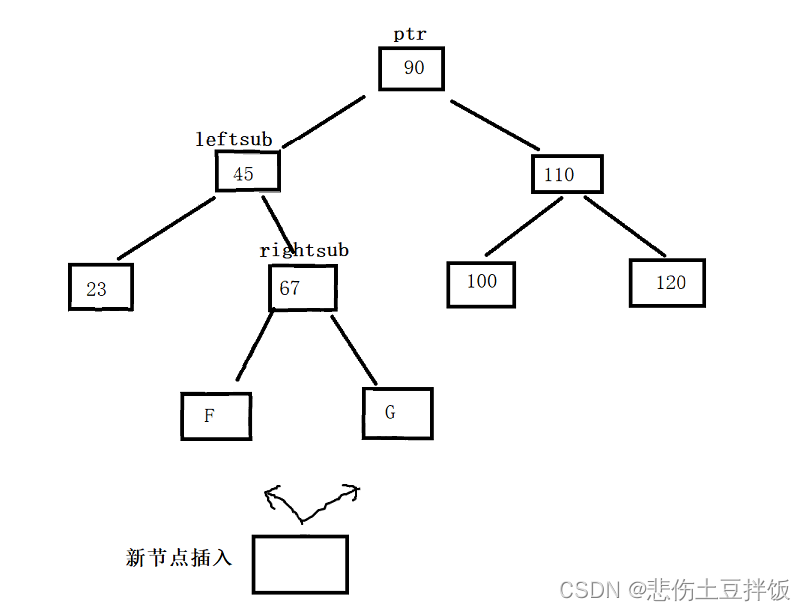
AVL树的插入与BST树的插入相似，但是需要进行高度平衡，继而要进行左右单旋转与左右双旋转，通过旋转还平衡二叉树，以及通过平衡因子的操作旋转，上图为左双旋转的实例，无论新节点插入F,或者G都需要进行左双旋转，因为ptr、leftsub、rightsub 组成了一个折线

typedef int KeyType;
typedef struct AVLNode
{
	KeyType key;
	struct AVLNode* leftchild;
	struct AVLNode* parent;
	struct AVLNode* rightchild;
	int balance;  //-1 0 1
}AVLNode, * AVLTree;


AVLNode* Buynode(KeyType kx)
{
	AVLNode* s = (AVLNode*)malloc(sizeof(AVLNode));
	if (s == NULL) exit(1);
	memset(s, 0, sizeof(AVLNode));
	s->key = kx;
	s->balance = 0;
	return s;
}
AVLNode* MakeRoot(KeyType kx)
{
	AVLNode* s = Buynode(kx);
	s->key = kx;
	return s;
}
void RotateLeft(AVLTree& tree, AVLNode* ptr)
{
	AVLNode* newroot = ptr->rightchild;
	newroot->parent = ptr->parent;

	if (newroot->leftchild != nullptr)
	{
		newroot->leftchild->parent = ptr;
	}
	ptr->rightchild = newroot->leftchild;

	newroot->leftchild = ptr;
	if (ptr == tree)
	{
		tree = newroot;
	}
	else
	{
		if (ptr->parent->leftchild == ptr)
		{
			ptr->parent->leftchild = newroot;
		}
		else
		{
			ptr->parent->rightchild = newroot;
		}
	}

	ptr->parent = newroot;
}
void RotateRight(AVLTree& tree, AVLNode* ptr)
{
	AVLNode* newroot = ptr->leftchild;
	newroot->parent = ptr->parent;
	ptr->leftchild = newroot->rightchild;
	if (newroot->rightchild != nullptr)
	{
		newroot->rightchild->parent = ptr;
	}
	
	newroot->rightchild = ptr;
	if (ptr == tree)
	{
		tree = newroot;
	}
	else
	{
		if (ptr->parent->leftchild == ptr)
		{
			ptr->parent->leftchild = newroot;
		}
		else
		{
			ptr->parent->rightchild = newroot;
		}
	}

	ptr->parent = newroot;
}
void RightBalance(AVLTree& tree, AVLNode* ptr)  //右双旋转  左双旋的镜像
{	
	AVLNode* rightsub = ptr->rightchild, * leftsub = nullptr;
	switch (rightsub->balance)
	{
	case 0: cout << "right balance" << endl; break;
	case 1:   
		ptr->balance = 0;
		rightsub->balance = 0;
		RotateLeft(tree, ptr);//左上右下的一条斜线 进行左单旋   下面左双旋的时候同理
		break;
	case -1:   
		leftsub = rightsub->leftchild;
		switch (leftsub->balance)
		{
		case -1: 
			rightsub->balance = 1 ; 
			ptr->balance = 0;     
			break;
		case 1: 
			rightsub->balance = 0;
			ptr->balance = -1;  
			break;
		case 0:   
			rightsub->balance = 0;
			ptr->balance = 0;
			break;
		}  
		leftsub->balance = 0; 
		RotateRight(tree, rightsub);
		RotateLeft(tree, ptr);  
		break;
	}
}
void LeftBalance(AVLTree& tree, AVLNode* ptr)
{
	//传入的ptr是平衡因子为-2的结点
	AVLNode* leftsub = ptr->leftchild, * rightsub = nullptr;
						//  根节点的左边 折线的中间节点
	switch (leftsub->balance)
	{
	case 0: cout << "left balance" << endl; break;
	case -1:   //向左延申的直线
		ptr->balance = 0;
		leftsub->balance = 0;
		RotateRight(tree, ptr); 
		break;
	case 1:    //一条折线 左双旋转
		rightsub = leftsub->rightchild;
		//根节点左边的右边，折线的下面节点
		switch (rightsub->balance)
		{
		case -1:  //插入在左边
			leftsub->balance = 0; //原本ptr的左孩子 现在也是ptr的左孩子
			ptr->balance = 1;     //ptr做双旋后变为了右孩子
			break;
		case 1:   //插入在右边
			leftsub->balance = -1;
			ptr->balance = 0;
			break;
		case 0:   //左双旋转后为0
			leftsub->balance = 0;
			ptr->balance = 0;
			break;
		}
		rightsub->balance = 0; //最终作根的结点，树两边高度相同
		RotateLeft(tree, leftsub);//左单旋转  ptr(最上面节点)是折线中间节点
		RotateRight(tree, ptr);   //右单旋转  ptr 是折线上面节点
		break;
	}
}
void PassBalance(AVLTree& tree, AVLNode* p)
{
	AVLNode* pa = p->parent;
	bool tall = true; //判断高度是否变化
	for (; pa != nullptr && tall;)
	{
		if (pa->leftchild == p) //判断左孩子或右孩子
		{
			switch (pa->balance)
			{
			case 0: pa->balance = -1; break;
			case 1: pa->balance = 0; tall = false;  break;
			case -1: 
				LeftBalance(tree, pa);
				tall = false;
				break;
			}
		}
		else
		{
			switch (pa->balance)
			{
			case 0: pa->balance = 1; break;
			case -1: pa->balance = 0; tall = false; break;
			case 1:
				RightBalance(tree, pa);
				tall = false;
				break;
			}
		}
		p = pa;
		pa = p->parent;
	}
}
bool Insert(AVLNode*& tree, KeyType kx)
{
	if (tree == nullptr)
	{
		tree = MakeRoot(kx);
		return true;
	}
	AVLNode* pa = nullptr;
	AVLNode* p = tree;
	while (p != nullptr && p->key != kx)
	{
		pa = p;
		p = kx < p->key ? p->leftchild : p->rightchild;
	}
	if (p != nullptr && p->key == kx) return false;
	p = Buynode(kx);
	p->parent = pa;
	if (kx < pa->key)
	{
		pa->leftchild = p;
	}
	else
	{
		pa->rightchild = p;
	}
	PassBalance(tree, p); //回溯
	return true;
}
void InOrder(AVLNode* ptr)
{
	if (ptr != nullptr)
	{
		InOrder(ptr->leftchild);
		cout << ptr->key << " " << ptr->balance << endl;
		InOrder(ptr->rightchild);
	}
}


int main()
{
	int ar[] = { 12,23,34,45,56,67,78,89,90,100 };
	AVLTree root = nullptr;
	for (auto& x : ar)
	{
		cout << Insert(root, x) << endl;
	}
	InOrder(root);
	cout << endl;
	return 0;
}

AVL 树的删除

如果被删除的节点 x 最多只有一个子女，那么问题比较简单，如果被删除节点 x 右两个子女，首先搜索 x 在中序次序下的直接前驱 y （同样可以找直接后继）；再把节点 y 的内容传送给结点 x ，现在问题转移到删除结点 y ，把结点 y 当作被删除的结点 x

将结点 x 从树中删去，因为结点 x 最多右一个子女，那么我们可以简单地把 x 的双亲结点中原来指向 x 的指针改指到这个子女结点；如果结点 x 没有子女，x 双亲结点的相应指针置为 NULL，然后将原来以结点 x 为根的子树的高度减 1

• 必须沿 x 通过向根路径反向追踪高度的变化对路经上各个结点的影响
• 用一个布尔遍历 shorter 来指向子树的高度是否被缩短，在每个结点上要做的操作取决于 shorter 的值和结点的 balance 有时还要依赖子女的 balance
• 布尔变量 shorter 的值初始化为 True，然后对于从 x 的双亲到根的路径上的各个结点 p，在shorter 保持为 True 时执行下面的操作，如果 shorter 变成 False，算法终止

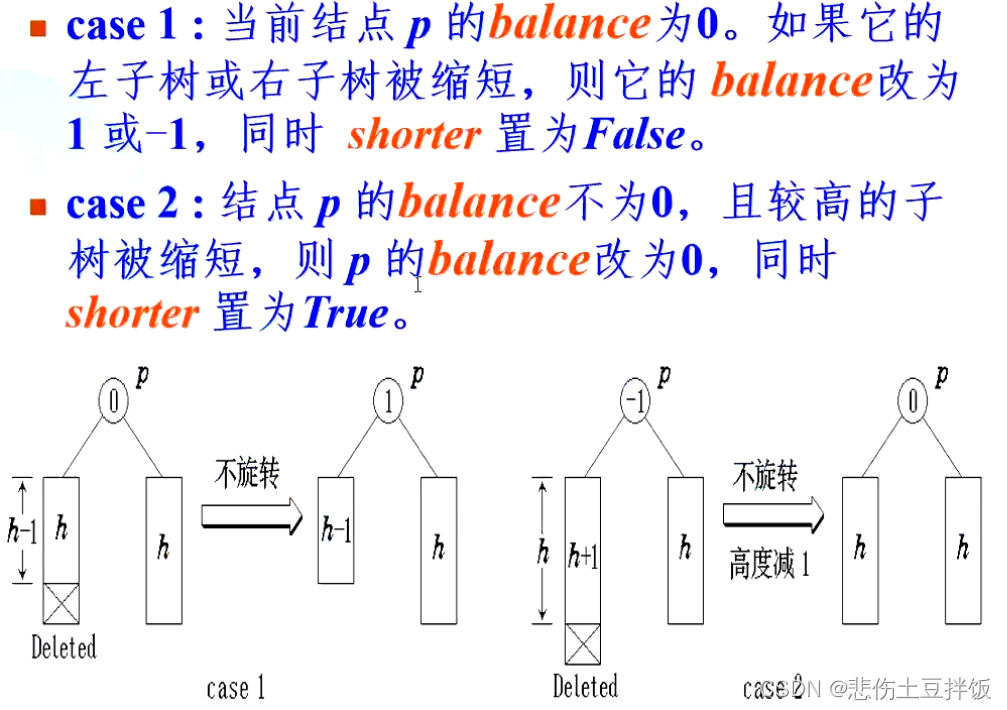
case 1：虽然删掉节点使得p的平衡因子变为了1，但是对于树的总体高度没有变化，依旧为h
case 2：当删掉节点后，p的平衡因子变为0，但是该树的总体高度由h+1变为了h，使得其父亲结点的平衡因子也会随之变化，那么就需要进行回溯

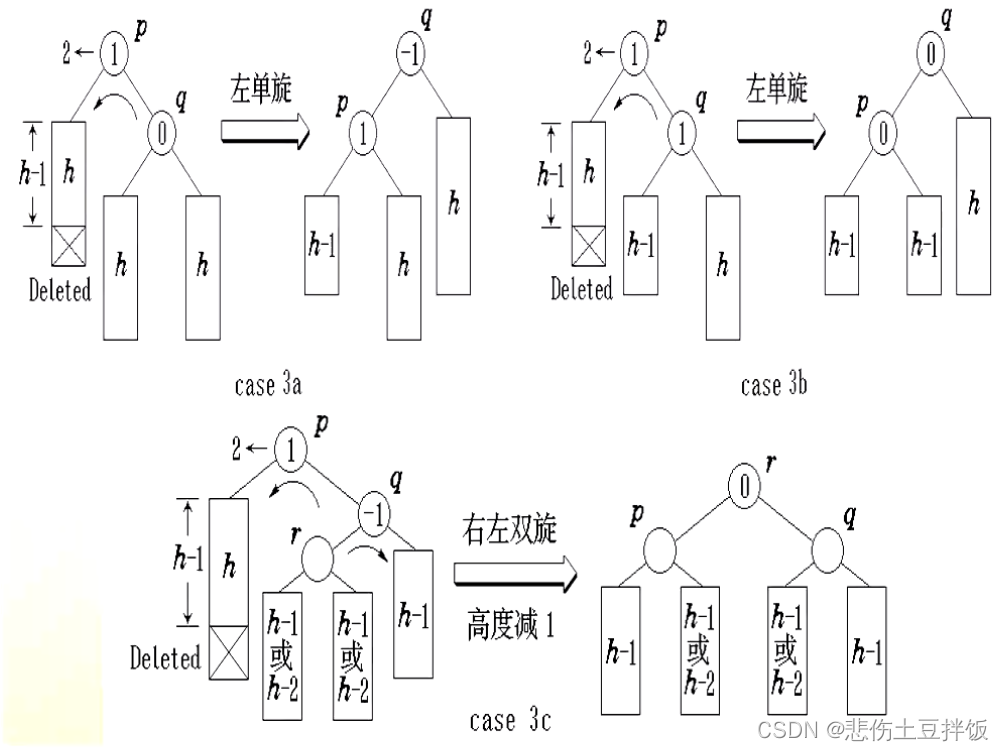
总结来说，就是要分析在平衡树的过程中是否对树的总体高度进行了影响，如果影响到了就需要进行回溯

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖