回溯算法–python实现n皇后问题

文章目录

回溯算法--python实现n皇后问题

什么是回溯法？

? 回溯法有“通用的解题法”之称。用它可以系统地搜索一个问题的所有解或任一解。回溯法是一个既带有跳跃性的搜索算法。它在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先策略搜索。回溯法求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。

回溯和递归是相辅相成的，回溯一般隐藏在递归函数的下面。
暴力法搜索

回溯法可以解决的问题？

组合问题 1234 12.13.14.23.24.34

切割问题如何切割字串是回文子串

子集问题 1234 1.2.3.4.12.13.14.23.24.34.123.124 …

排列问题

棋盘问题 n皇后，解数组

n后问题——问题描述

问题描述：在n X n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n X n格的棋盘上放置n个皇后，任何2个皇后不放在同一行或同一列或同一斜线。

列出n后问题所有的解。

假设一个2皇后的问题，不考虑攻击的条件，会有4（n^n）种解法。

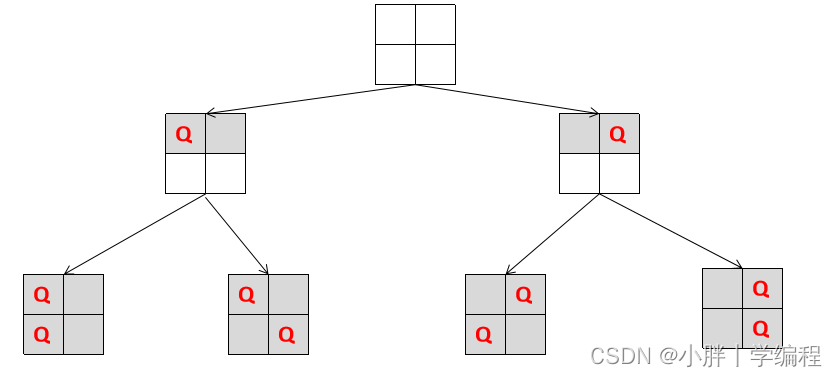
在这里插入图片描述

假设一个3皇后的问题，不考虑攻击的条件，会有27（n^n）种解法。

考虑攻击条件：

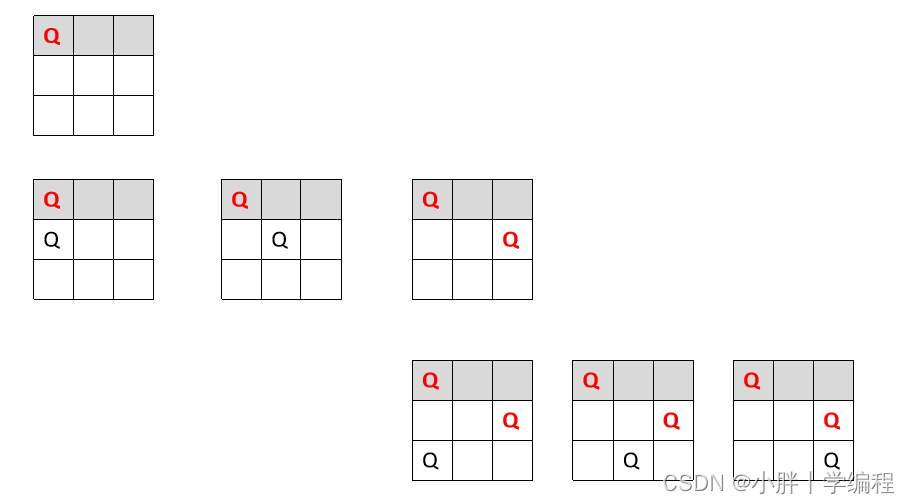
在这里插入图片描述

3*3=27

n*check(函数)

n后问题——解题思路

? 要解决N皇后问题，其实就是要解决好怎么放置这n个皇后，每一个皇后与前面的所有皇后不能在同一行、同一列、同一对角线，在这里我们可以以行优先，就是说皇后的行号按顺序递增，只考虑第i个皇后放置在第i行的哪一列，所以在放置第i个皇后的时候，可以从第1列判断起，如果可以放置在第1个位置，则跳到下一行放置下一个皇后。如果不能，则跳到下一列…直到最后一列，如果最后一列也不能放置，则说明此时放置方法出错，则回到上一个皇后向之前放置的下一列重新放置。此即是回溯法的精髓所在。当第n个皇后放置成功后，即得到一个可行解，此时再回到上一个皇后重新放置寻找下一个可行解…如此后，即可找出一个n皇后问题的所有可行解。

回溯模板——伪代码实现

List<value> result;
void backtrace(路径, 选择列表){
    if(满足结束条件){
        result.add(路径);
        return;
    }
    for(选择：选择列表){
        没有选择：
            跳出循环
        有选择：
            做选择
        backtrace(路径,选择列表);
        撤销选择;
    }
}

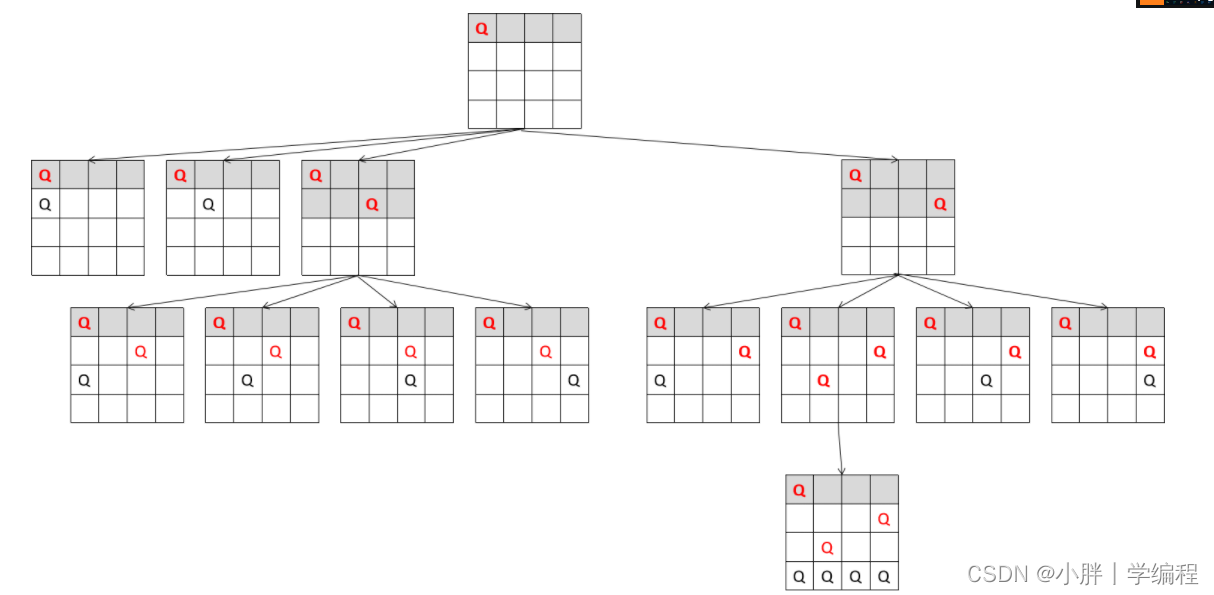
在这里插入图片描述

n后问题——复杂度分析

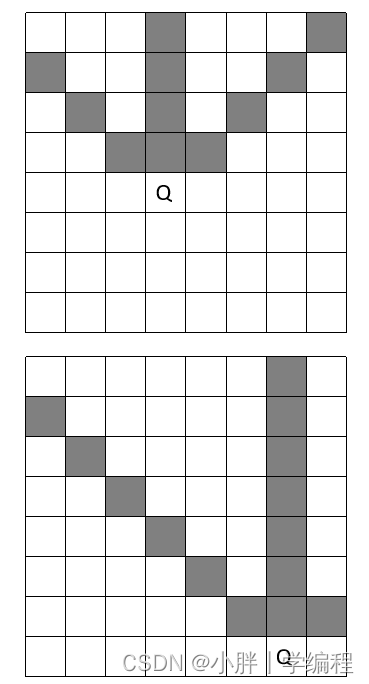
在这里插入图片描述

复杂度分析：
关于N皇后问题的复杂度问题可以说是众说纷纭了：在不进行剪枝的时候，我们可以认为是**O(n^n)**。
1.它在摆放皇后的时候，一次选取的是一行，因为同一行会攻击。
2.放入下一个的时候，动态的确定哪一行可以放入皇后，3个方向上不能有皇后

O(N!)。
分析：使用一个数组记录每行放置的皇后的列下标，依次在每一行放置一个皇后。每次新放置的皇后都不能和已经放置的皇后之间有攻击：即新放置的皇后不能和任何一个已经放置的皇后在同一列以及同一条斜线上，并更新数组中的当前行的皇后列下标。当 N个皇后都放置完毕，则找到一个可能的解。当找到一个可能的解之后，将数组转换成表示棋盘状态的列表，并将该棋盘状态的列表加入返回列表。
由于每个皇后必须位于不同列，因此已经放置的皇后所在的列不能放置别的皇后。第一个皇后有 N 列可以选择，第二个皇后最多有 N?1 列可以选择，第三个皇后最多有 N-2 列可以选择（如果考虑到不能在同一条斜线上，可能的选择数量更少），因此所有可能的情况不会超过 N!种，遍历这些情况的时间复杂度是 O(N!)。

List<value> result;
void backtrace(路径, 选择列表){
    if(满足结束条件){
        result.add(路径);
        return;
    }
    for(选择：选择列表){
        没有选择：
            跳出循环
        有选择：
            做选择
        backtrace(路径,选择列表);
        撤销选择;
    }
}

for 循环 O(n)

check O(n)

backtrace O(n^2)

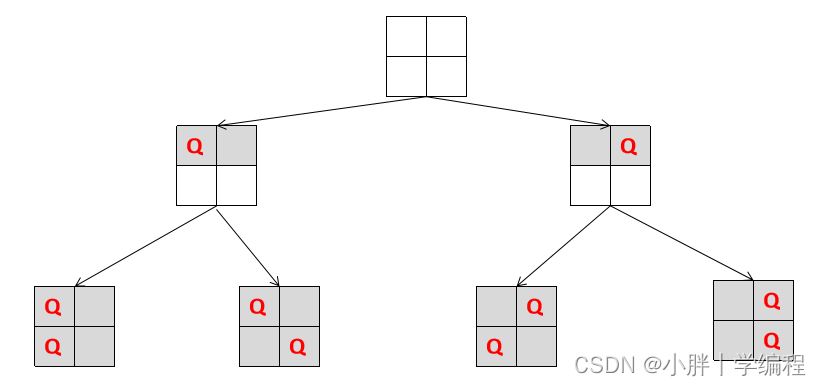
在这里插入图片描述

n^n次方的调用次数

n^n * O(n^2)

具体的不太好算，没有重叠的子问题。

n后问题——实现代码

确定递归的终止条件: n个皇后都放入进去了

确定单层搜索的逻辑：三个方向没有皇后，继续递归，否则跳出当前。0

List<value> result;
void backtrace(路径, 选择列表){
    if(满足结束条件){
        result.add(路径);
        return;
    }
    for(选择：选择列表){
        没有选择：
            跳出循环
        有选择：
            做选择
        backtrace(路径,选择列表);
        撤销选择;
    }
}

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        res = []
        trans = lambda path: ['.'*i + 'Q' + '.'*(len(path)-1-i) for i in path]
        def recursion(n, path, pos):
            if len(path) == n:
                res.append(trans(path))
                return 
            l,r,m=pos
            l, r = [i-1 for i in l], [i+1 for i in r]
            total = l + r + m
            for cand in range(n):
                if cand in total:
                    continue
                recursion(n, path+[cand],[l+[cand], r+[cand], m+[cand]])
        recursion(n, [], [[],[],[]])
        return res