邻接表
邻接表的构造与邻接矩阵完全不同,同学们应该发现了,邻接表的的结构更像是由几个链表构成的。
在构造邻接表时,我们的确会借助链表的结构。对图中每个顶点的信息,我们都会分别使用一个链表来进行存储。因此,我们需要初始化一个有 n 个元素的链表数组, n 为图中顶点数量。
我们要在邻接表中存储的图的信息,实际上就是顶点之间存在的有向边。当从顶点 a 到顶点 b 存在一条有向边时,我们只需要在头结点为 a 的链表后插入一个结点 b。值得注意的是,当一条边是从顶点 b 到顶点 a 时,我们同样需要在以 b 为头结点的链表后插入一个结点 a。
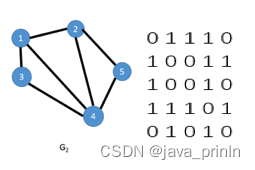
同样在输出邻接表的时候,我们也只需要把每个链表依次遍历输出就好了。链表插入和输出的方法在第二章链表里已经学习过了,在这里我们就不再重复,那么接下来我们就来学习怎么实现邻接表吧。
邻接表的构造
我们已经为你实现了一个带有插入功能的链表,接下来,请使用这个现成的链表结构体, 构造出一个图的邻接表结构, 也就是 Graph 结构体及其相关函数。
首先,我们来定义 Graph 结构体的成员,邻接表需要保存每个顶点相邻的所有边的信息,就像下图中这个例子:
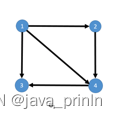
用邻接表保存的结果为:
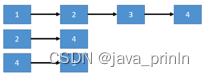
也就是对每个顶点,都需要一个链表来保存。我们先在Graph 结构体里 定义一个大小为 MAX_N 的链表数组edges.
2. 定义完链表数组以后,我们还需要再定义一个 int 类型的成员变量n , 用来保存图中顶点数量。
3. 接下来,去实现Graph 的 初始化函数 init. 首先定义一个空的初始化函数,函数没有返回值,有两个参数,一个是Graph 类型的指针参数g, 另一个是 int 类型的参数n, 表示输入的图中顶点数量。
4. 接下来就要实现初始化函数的具体逻辑了。首先,将输入的图中顶点数量保存到Graph 结构体的成员变量中。
5. 接下来我们要把n 个链表循环初始化,初始均指向NULL. 我们先写一个 for 循环,用int 类型的变量 i 从 0 循环到不小于 g->n 时退出,在循环内实现将 每个链表 g->edges[i] 赋值为NULL 的操作。
6. 这样我们就完成了 初始化函数 init , 接下来我们在 main 函数中定义一个 Graph 类型的指针变量 graph , 并 申请一个 Graph 类型的内存空间, 然后调用初始化函数 init 完成对 graph 的初始化,参数大小设为 100.
7. 与邻接矩阵不同, 我们在构造邻接表时利用了 链表的结构。 所以,在程序结束前,我们还需要去释放链表占用的内存空间。 我们可以使用一个函数来实现它。
8. 首先在主函数之前定义一个没有返回值,参数为一个Graph 类型的指针变量 g 的函数 clear.
9. 在clear 函数中, 我们使用变量 i 从 0 循环到不小于 g->n 时 退出来遍历所有链表。
10. 在每次循环中, 我们可以先定义一个Node 类型的指针变量 head 来 指向 每个 链表。 接着我们从头节点不断向后查找并删除每一个结点。 我们可以用while 循环来实现这一个逻辑,当head 不为空时则指向后一个结点, 这里我们先把while 循环的条件写好。
11. 在while 循环中, 我们先用法一个Node 类型的指针变量 delede_node 保存当前结点head , 然后让head 指向它的后一个结点,最后使用free 来释放 delete_node 指向的内存空间。
12. 在循环结束后,别完了释放指针 9 指向的内存空间。
13. 最后, 我们还需要在主函数调用 clear 来释放 graph 占用的内存。
14.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_N 10000
typedef struct Node {
int vertex;
struct Node *next;
} Node, *LinkedList;
LinkedList insert_node(LinkedList head, int index) {
Node *node = (Node *)malloc(sizeof(Node));
node->vertex = index;
node->next = head;
head = node;
return head;
}
typedef struct Graph {
LinkedList edges[MAX_N];
int n;
} Graph;
// 请在下面实现初始化函数
void init(Graph *g, int n) {
g->n = n;
for(int i = 0; i < g->n; ++i) {
g->edges[i] = NULL;
}
}
// 请在下面实现函数 clear
void clear(Graph *g) {
for(int i = 0; i < g->n; ++i) {
Node *head = g->edges[i];
while (head != NULL) {
Node *delete_node = head;
head = head->next;
free(delete_node);
}
}
free(g);
}
int main() {
Graph *graph = (Graph *) malloc(sizeof(Graph));
init(graph, 100);
clear(graph);
return 0;
}
邻接表的使用
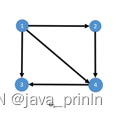
用邻接表保存的结果为:
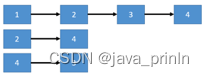
也就是说,当插入一条从x 连向 y 的边时, 要将y 的值插入到x 对应的链表中。在插入前,我们还是先来判断一下插入的X 是否合法, 如果x 不在区间[0, g-> n] 内或者 y 不在区间 [0, g-> n ] 内, 则直接结束函数。
2. 链表LinkedList 的插入函数是insert_node , 传入两个参数, 一个参数head 表示的操作链表,另一个参数 index 表示新插入的链表结点的值。
3. 现在,请在 insert 函数里实现有向边的插入操作吧。
4. 下面我们要实现邻接表的输入了。对于下面这个邻接表:
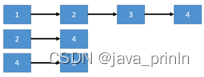
我们要在终端里输出:
1:2 3 4
2:4
3:
4:3
首先,在输出函数里让循环变量i 从 0 循环到不小于g->n 时退出,并在循环体内部输出 i 和 紧随其后的一个冒号吧,注意是英文的冒号。
在循环内部,要依次输出每个链表所有元素的值。定义一个Node * 类型的循环变量j, 初值为链表 g->edges[i] 的表头,终值为NULL, 循环变量j 通过它指向的Node 内的next 指针获得下一个链表内元素的地址。
先把for 循环的头部实现吧,记得加上一对大口号。
5. 接下来,我们要在内存的循环体实现邻接表元素的输出。链表内结点的值保存为 vertex, 所以输出循环变量指向的vertex 值就可以了, 输出值以后再紧跟着输出一个空格。
6. 现在距离最终完成仅剩一步之遥。我们在每次输出完整个链表后,再输出一个空行。
7.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_N 10000
typedef struct Node {
int vertex;
struct Node *next;
} Node, *LinkedList;
LinkedList insert_node(LinkedList head, int index) {
Node *node = (Node *)malloc(sizeof(Node));
node->vertex = index;
node->next = head;
head = node;
return head;
}
typedef struct Graph {
LinkedList edges[MAX_N];
int n;
} Graph;
void init(Graph *g, int n) {
g->n = n;
for (int i = 0; i < g->n; ++i) {
g->edges[i] = NULL;
}
}
void insert(Graph *g, int x, int y) {
if (x <0 || x>= g->n || y < 0 || y >= g->n ) {
return ;
}
g->edges[x] = insert_node(g->edges[x], y);
}
void output(Graph *g) {
for(int i = 0; i < g->n; ++i) {
printf("%d:", i);
for(Node *j = g->edges[i]; j != NULL; j= j->next){
printf("%d ", j->vertex);
}
printf("\n");
}
}
void clear(Graph *g) {
for (int i = 0; i < g->n; ++i) {
Node *head = g->edges[i];
while (head != NULL) {
Node *delete_node = head;
head = head->next;
free(delete_node);
}
}
free(g);
}
int main() {
int n, m, x, y;
scanf("%d %d", &n, &m);
Graph *graph = (Graph *)malloc(sizeof(Graph));
init(graph, n);
for (int i = 0; i < m; ++i) {
scanf("%d %d", &x, &y);
insert(graph, x, y);
}
output(graph);
clear(graph);
return 0;
}
