题目链接:Problem - 3535
样例输入:
3 3
2 1
2 5
3 8
2 0
1 0
2 1
3 2
4 3
2 1
1 1
3 4
2 1
2 5
3 8
2 0
1 1
2 8
3 2
4 4
2 1
1 1
1 1
1 0
2 1
5 3
2 0
1 0
2 1
2 0
2 2
1 1
2 0
3 2
2 1
2 1
1 5
2 8
3 2
3 8
4 9
5 10样例输出:
5
13
-1
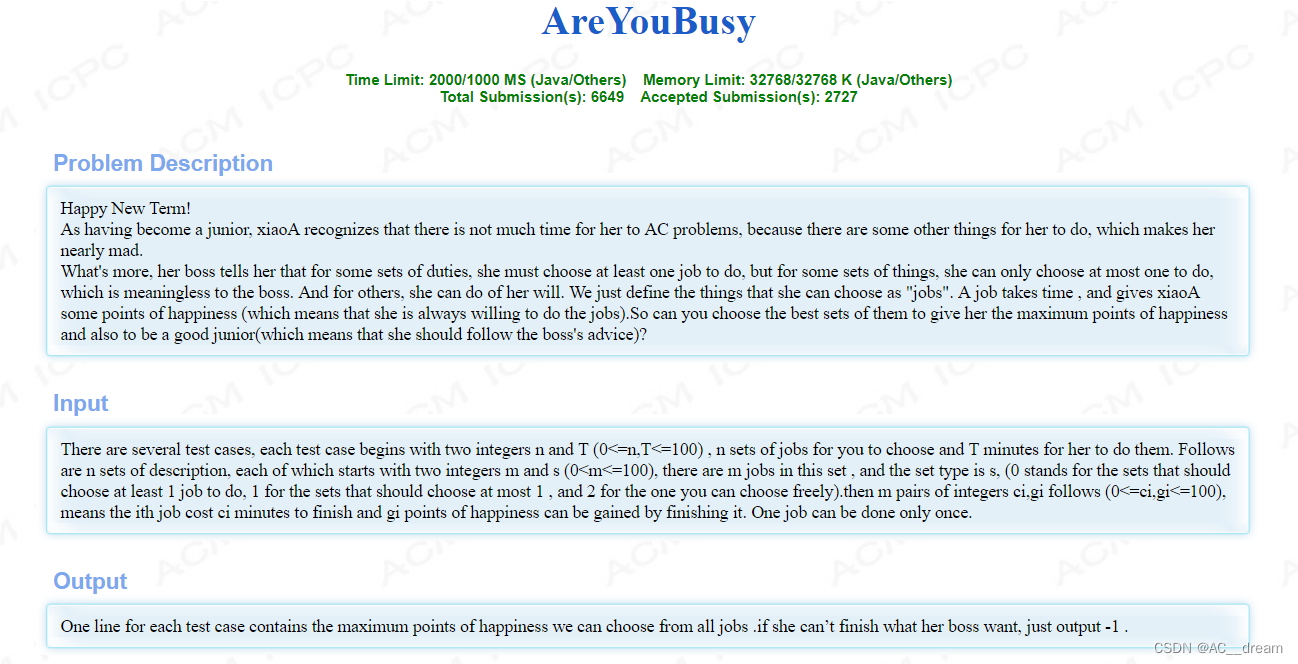
-1分析:这是一个混合背包问题,先分成若干组,再对每组内的物品进行限制,限制有以下三种,我们逐个进行分析:
设f[i][j]表示考虑前i组且体积为j在满足所有限制的情况下所能获得的最大价值。
第一个限制:至少选择该组中的一个作业,在这个组中我们只需要区别是否有作业被选择,这就是一个特殊的完全背包问题,只需要改一下初始化条件,一开始我们肯定是要把f[o][i]设置为负无穷大。只要最后更新完该组物品发现所有f[o][i]依然为负无穷说明无法满足该组的要求,那么更新到最后f数组一定也是趋向于负无穷大的,那么也就是说最后是否满足老板要求的判断依据就是看f数组的值是否为正。
第二个限制:最多选择一个作业,那么我们就可以把该组物品当作01背包来做,把每个物品都当作一个新的物品,在前o-1组的物品的选取基础上进行选取,结果只有选或者不选
第三个限制:选任意多个作业,这个直接当作一个完全背包来更新就行了,因为并没有强制要求选多少的限制,所以直接在前o-1组物品的选取基础上进行完全背包的更新即可。
我们看第一个限制和第三个限制都是当成完全背包来处理,但是区别就是初始化值的不同,由于第一个限制至少要选取一个物品,所以f[o][i]应该初始化为负无穷,若更新后不为负无穷说明选取了物品即满足了该限制,而第三个限制并没有具体说明选取物品的多少,所以一开始初始化就是初始化为上一组物品的选取情况。
下面是代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
const int N=1e4+3,M=103;
int f[M][N];//f[i][j]表示考虑前i组物品用体积为j所能得到的最大价值
int v[M],cost[M];
int main()
{
int n,t,m,s;
while(scanf("%d%d",&n,&t)!=EOF)
{
memset(f,0,sizeof(f));
for(int o=1;o<=n;o++)
{
scanf("%d%d",&m,&s);
for(int i=1;i<=m;i++)
scanf("%d%d",&cost[i],&v[i]);
if(s==1)//最多选择一个作业,相当于对每个作业进行01背包选取
{
for(int i=0;i<=t;i++) f[o][i]=f[o-1][i];
for(int i=1;i<=m;i++)
for(int j=t;j>=cost[i];j--)
f[o][j]=max(f[o][j],f[o-1][j-cost[i]]+v[i]);
}
else
{
if(s==0)//至少选择一个作业
for(int i=0;i<=t;i++) f[o][i]=-0x3f3f3f3f;
else//随意选择任意个作业,相当于对每个背包进行完全背包选取
for(int i=0;i<=t;i++) f[o][i]=f[o-1][i];
for(int i=1;i<=m;i++)
for(int j=t;j>=cost[i];j--)
{
f[o][j]=max(f[o][j],f[o][j-cost[i]]+v[i]);
f[o][j]=max(f[o][j],f[o-1][j-cost[i]]+v[i]);
}
}
}
printf("%d\n",f[n][t]>-1?f[n][t]:-1);//取与-1的最大值
//如果存在一个o使得所有的f[o][i]均为-0x3f3f3f3f,那么最后的f[n][t]一定小于-1
}
return 0;
}