核心思想:快慢指针
思路:
题干要求空间复杂度O(1),时间复杂度O(n)。
如果数组中没有重复的数,以数组 [1,3,4,2]为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)f(n),
其映射关系 n->f(n)为:
0->1
1->3
2->4
3->2
我们从下标为 0 出发,根据 f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推,直到下标超界。这样可以产生一个类似链表一样的序列。
0->1->3->2->4->null
如果数组中有重复的数,以数组 [1,3,4,2,2] 为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)f(n),
其映射关系 n->f(n) 为:
0->1
1->3
2->4
3->2
4->2
同样的,我们从下标为 0 出发,根据 f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推产生一个类似链表一样的序列。
0->1->3->2->4->2->4->2->……
这里 2->4 是一个循环,那么这个链表可以抽象为下图:
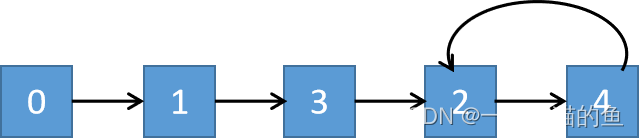
从理论上讲,数组中如果有重复的数,那么就会产生多对一的映射,这样,形成的链表就一定会有环路了。
综上
1.数组中有一个重复的整数 <> 链表中存在环
2.找到数组中的重复整数 <> 找到链表的环入口
参考LeetCode 热题100-51-环形链表Ⅱ,由a+b=2(a+b)以及a+b=a+k(b+c)可得:
a=c+(n?1)(b+c)
我们会发现:从相遇点到入环点的距离c加上 n-1 圈的环长,恰好等于从链表头部到入环点的距离,相当于a的长度等于相遇点开始走n-1圈,再走c的距离。所以,再找到相遇点之后,将slow慢指针重新指向0位置,将fast快指针指向相遇点(相遇点距离入环点b的距离,再走c+(n?1)(b+c),不久正好到入环点了,长度也等于a)。
class Solution {
public int findDuplicate(int[] nums) {
int slow = 0;
int fast = 0;
slow = nums[slow];
fast = nums[nums[fast]];
while(slow != fast){
slow = nums[slow];
fast = nums[nums[fast]];
}
int pre1 = 0;
int pre2 = fast;
while(pre1 != pre2){
pre1 = nums[pre1];
pre2 = nums[pre2];
}
return pre1;
}
}
我的方法:空间复杂度较高
class Solution {
public int findDuplicate(int[] nums) {
HashSet<Integer> hashset = new HashSet<>();
for(int i = 0; i < nums.length; i++){
if(!hashset.contains(nums[i])){
hashset.add(nums[i]);
}else{
return nums[i];
}
}
return 0;
}
}
