给定一个由?0?和?1?组成的矩阵?mat?,请输出一个大小相同的矩阵,其中每一个格子是?mat?中对应位置元素到最近的?0?的距离。两个相邻元素间的距离为?1?。
示例 1:
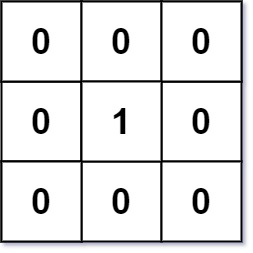
输入:mat = [[0,0,0],[0,1,0],[0,0,0]] 输出:[[0,0,0],[0,1,0],[0,0,0]]
示例 2:
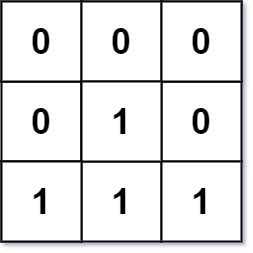
输入:mat = [[0,0,0],[0,1,0],[1,1,1]] 输出:[[0,0,0],[0,1,0],[1,2,1]]
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j] is either 0 or 1.mat?中至少有一个?0
?注:本题可以使用动态规划方法,计算当前位置和周围点的距离,具体的来说,从左到右移动从上到下遍历我们可以分为两种情况,如下图所示,一种是水平向左和竖直向上移动,一种是水平向右和竖直向下移动。这两种情况可以覆盖所有。

class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int n = mat.size(), m = mat[0].size();
vector<vector<int>> tmp(n, vector<int> (m,INT_MAX / 2));
for(int i=0; i < n; i++){
for(int j = 0; j < m; j++){
if(mat[i][j] == 0){
tmp[i][j] = 0;
}
}
}
//动态规划
//水平向左和竖直向上移动
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(i - 1 >= 0){
tmp[i][j] = min(tmp[i][j],tmp[i-1][j]+1);
}
if(j - 1 >= 0){
tmp[i][j] = min(tmp[i][j],tmp[i][j-1]+1);
}
}
}
//水平向右和竖直向下移动
for(int i = n - 1; i >= 0; i--){
for(int j = m-1; j >= 0; j--){
if(i + 1 < n){
tmp[i][j] = min(tmp[i][j],tmp[i+1][j]+1);
}
if(j + 1 < m){
tmp[i][j] = min(tmp[i][j],tmp[i][j+1]+1);
}
}
}
return tmp;
}
};在给定的?m x n?网格?grid?中,每个单元格可以有以下三个值之一:
- 值?
0?代表空单元格; - 值?
1?代表新鲜橘子; - 值?
2?代表腐烂的橘子。
每分钟,腐烂的橘子?周围?4 个方向上相邻?的新鲜橘子都会腐烂。
返回?直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回?-1?。
示例 1:
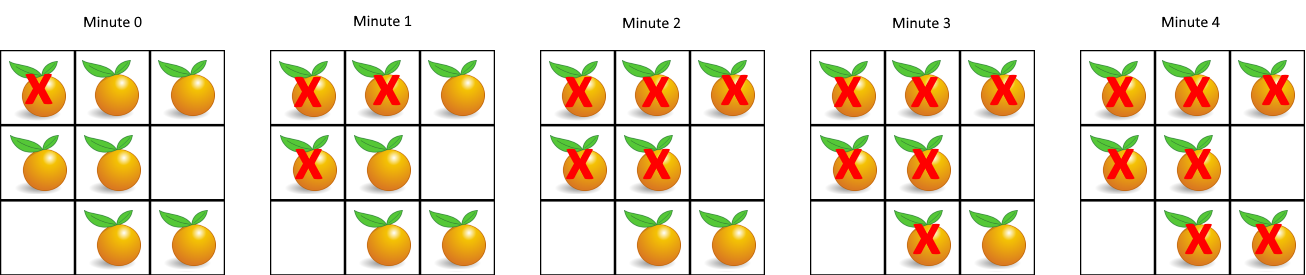
输入:grid = [[2,1,1],[1,1,0],[0,1,1]] 输出:4
示例 2:
输入:grid = [[2,1,1],[0,1,1],[1,0,1]] 输出:-1 解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
输入:grid = [[0,2]] 输出:0 解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j]?仅为?0、1?或?2
注:本题可以使用广度优先搜索,就是从起点出发,每次都尝试访问同一层的节点,如果同一层都访问完了,再访问下一层,最后广度优先搜索找到的路径就是从起点开始的最短合法路径。假设图中只有一个腐烂的橘子,它每分钟向外拓展,腐烂上下左右相邻的新鲜橘子,那么下一分钟,就是这些被腐烂的橘子再向外拓展腐烂相邻的新鲜橘子,这与广度优先搜索的过程均一一对应,上下左右相邻的新鲜橘子就是该腐烂橘子尝试访问的同一层的节点,路径长度就是新鲜橘子被腐烂的时间。我们记录下每个新鲜橘子被腐烂的时间,最后如果单元格中没有新鲜橘子,腐烂所有新鲜橘子所必须经过的最小分钟数就是新鲜橘子被腐烂的时间的最大值。?
class Solution {
int cnt;
int dis[10][10];
int dir_x[4]={0, 1, 0, -1};
int dir_y[4]={1, 0, -1, 0};
public:
int orangesRotting(vector<vector<int>>& grid) {
queue<pair<int,int> >Q;
memset(dis, -1, sizeof(dis));
cnt = 0;
int n=(int)grid.size(), m=(int)grid[0].size(), ans = 0;
for (int i = 0; i < n; ++i){
for (int j = 0; j < m; ++j){
if (grid[i][j] == 2){
Q.push(make_pair(i, j));
dis[i][j] = 0;
}
else if (grid[i][j] == 1) cnt += 1;
}
}
while (!Q.empty()){
pair<int,int> x = Q.front();Q.pop();
for (int i = 0; i < 4; ++i){
int tx = x.first + dir_x[i];
int ty = x.second + dir_y[i];
if (tx < 0|| tx >= n || ty < 0|| ty >= m|| ~dis[tx][ty] || !grid[tx][ty]) continue;
dis[tx][ty] = dis[x.first][x.second] + 1;
Q.push(make_pair(tx, ty));
if (grid[tx][ty] == 1){
cnt -= 1;
ans = dis[tx][ty];
if (!cnt) break;
}
}
}
return cnt ? -1 : ans;
}
};
