题目要求

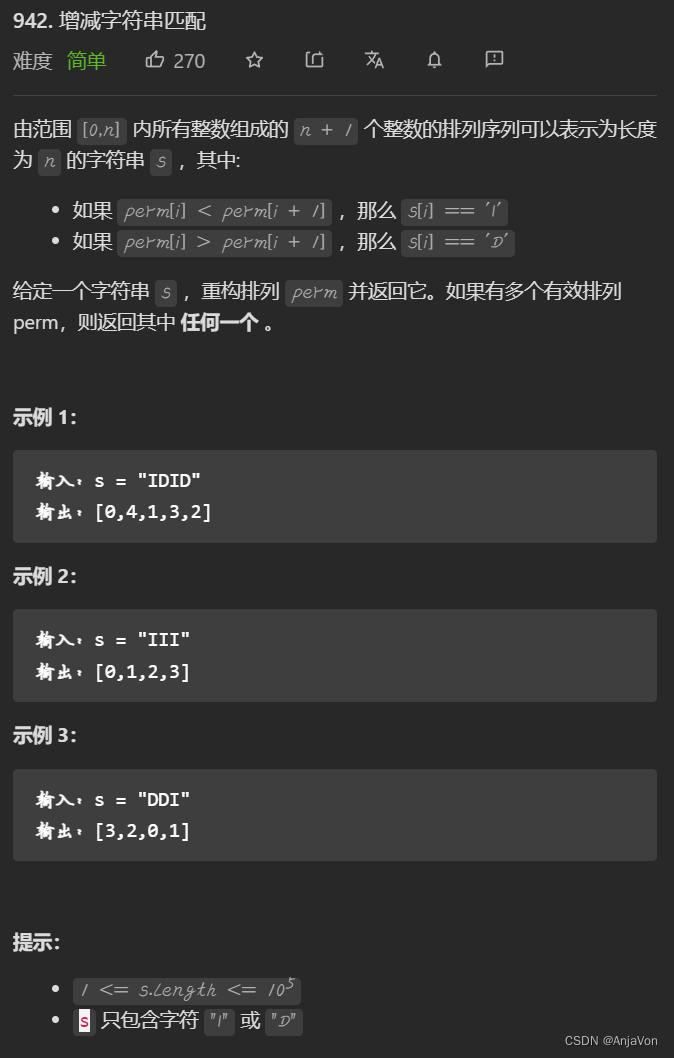
在这里插入图片描述

思路：贪心

每次都用当前区间内的边界构造，即看到I，就放当前可用的最小值；看到D，就放当前可用的最大值。
证明：
- 起始区间为 $[0, n]$ ， $n$ 为所给string大小；
- 当 $s [0] = I$ 时，填入左边界 $0$ （最小值），区间变为 $[1, n]$ ，即后续所有数都将比当前大，符合题意；
- 当 $s [1] = D$ 时，填入右边界 $n$ （最大值），区间变为 $[1, n ? 1]$ ，即后续所有数都将比当前小，符合题意。

Java

class Solution {
    public int[] diStringMatch(String s) {
        int n = s.length(), small = 0, large = n, idx = 0;
        int[] res = new int[n + 1];
        for(int i = 0; i < n; i++) {
            if(s.charAt(i) == 'I') // 放最小的
                res[idx++] = small++;
            else // 放最大的
                res[idx++] = large--;
        }
        res[idx] = small;
        return res;
    }
}

时间复杂度： $O (n)$
空间复杂度： $O (1)$

C++

class Solution {
public:
    vector<int> diStringMatch(string s) {
        int n = s.size(), small = 0, large = n, idx = 0;
        vector<int> res(n + 1);
        for(int i = 0; i < n; i++) {
            if(s[i] == 'I') // 放最小的
                res[idx++] = small++;
            else // 放最大的
                res[idx++] = large--;
        }
        res[idx] = small;
        return res;
    }
};

时间复杂度： $O (n)$
空间复杂度： $O (1)$

Rust

impl Solution {
    pub fn di_string_match(s: String) -> Vec<i32> {
        let mut res = vec![0; s.len() + 1];
        let (mut small, mut large) = (0, s.len() as i32);

        s.chars().enumerate().for_each(|(i, b)| if b == 'I' { // 放最小的
            res[i] = small;
            small += 1
        } else { // 放最大的
            res[i] = large;
            large -= 1
        });
        res[s.len()] = small;
        res
    }
}