开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 十一种排序算法全面解析 -> 正文阅读

[数据结构与算法]十一种排序算法全面解析

1. 排序相关概念

排序算法的评价：

时间复杂度：主要分析关键字的比较次数和记录的移动次数
空间复杂度：需要的辅助内存的大小
稳定性：假设数据在有两个2，这两个2排序之后的相对顺序不变

外部排序：需要借助外部存储器，如磁盘（多路归并排序）
内部排序：仅需要内存

内部排序类：

选择排序：直接选择排序、堆排序
交换排序：冒泡排序、快速排序
插入排序：直接插入排序、折半插入排序、希尔排序
归并排序
线性排序算法：计数排序、桶排序、基数排序

2. 选择排序

2.1 直接选择排序

特点：

n个数据需要n-1趟比较
升序：每次选取当前未处理元素中的最小元素放在数组前面
降序：每次选取当前未处理元素中的最大元素放在数组前面
不稳定排序
时间复杂度: 最好 $O(n^2) \quad$ 最坏 $O(n^2) \quad$ 平均 $O(n^2) \quad$
空间复杂度： $O (1)$

例子：对数据21 30 49 30* 16 9 加*号是为了判断排序之后数据是否稳定
在这里插入图片描述

package datastructure.sort;

import java.util.Arrays;
public class SelectSort {
	public static void sort(int[] arr) {
		int n=arr.length;
		//依次进行n-1趟比较  第i趟选择第i小的值放在位置i上
		for(int i=0;i<n-1;i++) {
			int minIndex=i;//假设当前最小数据就是arr[i]
			for(int j=i+1;j<n;j++) {//j=i+1: 第i个数据只和它后面的数据比较
				if(arr[j]<arr[minIndex]) {
					minIndex=j;//minIndex保存本趟比较中较小值的索引
				}
			}
			if(minIndex!=i) {//相等说明arr[i]就是当前最小 不用交换 不等需要交换
				int tmp=arr[i];
				arr[i]=arr[minIndex];
				arr[minIndex]=tmp;
			}
		}
		System.out.println(Arrays.toString(arr));
	}
	public static void main(String[] args) {
		int[] arr= {21,30,49,30,16,9};
		sort(arr);
	}
}

2.2 堆排序

堆排序相关内容参考：优先队列和堆及相关问题

特点：

时间复杂度: 最好 $\quad$ 最坏 $\quad$ 平均 $\quad$
空间复杂度：O(1）
不稳定排序

代码实现：

package datastructure.sort;

import java.util.Arrays;

public class HeapSort {
	public static void sort(int arr[])
    {
        int N=arr.length;
        //将数组元素构建出一个大顶堆
        //最后一个节点编号是N-1  其父节点编号为:(N-1-1)/2=N/2-1
        for(int k=N/2-1;k>=0;k--)// N/2-1指向最后一个父节点 从其开始调整
        {
            sink(arr,k,N);
        }
        
        //交换  下沉
        while(N>0)
        {
            swap(arr, 0, N-1);
            N--;//N--可以看出是删除堆顶最大元素 因此需要进行下沉操作进行调整
            sink(arr, 0, N);//这里只需要sink一次是因为只影响了堆顶节点和其左右子节点的关系
        }
        
        System.out.println(Arrays.toString(arr));

    }
   
    public static void sink(int arr[],int k,int N)
    {
        
        while(2*k+1<N)
        {
            int j=2*k+1;//指向左子节点
            //根节点>=max(左子节点，右子节点)
            if(j+1<N&&arr[j]<arr[j+1])//如果右子节点存在且右子节点比左子节点大 j+1指向右子节点 
                j++;//j指向右子节点
            if(arr[k]>=arr[j])//找到<=根节点的子节点 停止  
                break;
            swap(arr, k, j);
            k=j;
        }
    }
    public static void swap(int arr[],int i,int j)
    {
        int tmp=arr[i];
        arr[i]=arr[j];
        arr[j]=tmp;
    }
    public static void main(String[] args) {
    	int[] arr= {21,30,49,30,16,9};
		sort(arr);
	}

}

3. 交换排序

3.1 冒泡排序

特点：

n个数据需要n-1趟比较
第1趟需要n-1次比较，最后一趟只需要1次比较，即越往后比较次数越少
每趟比较结束后，都能确定一个元素到数组的后面
如果某一趟没有进行交换，说明数组已经排好序了
稳定排序
时间复杂度：平均： $O(n^2) \quad$ 最坏： $O(n^2) \quad$ 最好： $O (n)$ （使用了flag标志，如果数组本来就有序，第一趟比较后没有发生交换择排序结束）
空间复杂度：O(1)

例子：9 16 21* 23 30 49 21 30*
在这里插入图片描述

package datastructure.sort;

import java.util.Arrays;

public class BubbleSort {
	/*
	 * n个数据需要n-1趟处理
	 * 第一次趟处理需要比较n-1次
	 * 第二次趟处理需要比较n-2次
	 * ....
	 * 最后一次处理需要比较1次
	 */
	public static void sort(int[] arr) {
		int n=arr.length;
		for(int pass=n-1;pass>=1;pass--) {//一共要n-1趟
			boolean flag=false;
			for(int i=0;i<pass;i++) {
				if(arr[i]>arr[i+1]) {
					int tmp=arr[i];
					arr[i]=arr[i+1];
					arr[i+1]=tmp;
					flag=true;
				}
			}
			if(!flag)//如果某趟没有发生交换 说明已经排好序
				break;
		}
		System.out.println(Arrays.toString(arr));
	}
	public static void main(String[] args) {
		int[] arr= {2,3,1,7,6,5,8,0,9,4};
		sort(arr);
	}
}

3.2 快速排序

特点：

一种分治的排序算法
将一个数组分成两个子数组，将两部分独立地排序
一个很重要的过程就是切分partition,切分过程总能排定一个元素，每次进行切分时，可以用子数组的第一个元素作为切分元素，切分完完成后，该切分元素左边的元素都不大于切分元素，切分元素右边的元素都不小于切分元素（以升序为例）
不稳定排序
时间复杂度：平均： $\quad$ 最好： $\quad$ 最坏： $O(n^2)$ (最坏情况出现在每次切分的元素不能划分成两个子数组，比如数组有序，以第一个元素进行切分的话，实际上数组的规模并没有变小，为了解决这种情况，一般可以选随机选取一个元素，将该元素移动到数组首部或尾部作为切分元素，每次切分时都选取当前子数组中随机的一个元素)
空间复杂度： $\quad$ 最坏： $\quad$ 递归的栈空间

package datastructure.sort;

import java.util.Arrays;

public class QuickSort {
	public static void quickSort(int arr[],int lo,int hi)
    {
        if(hi<=lo)
            return;
        int j=partition(arr,lo,hi);//j左边的元素不大于a[j],j右边的元素不小于a[j]
        quickSort(arr,lo,j-1);
        quickSort(arr,j+1,hi);
    }
public static int partition(int arr[],int lo,int hi)
    {
        int i=lo;
        int j=hi+1;
        int v=arr[lo];//切分的元素
        while (true)
        {
            //保证切分元素左边的元素都比它小，右边的元素都比它大
            while (arr[++i]<v)//查找比切分元素大的元素a
                if(i==hi)
                    break;
            while (arr[--j]>v)//查找比切分元素小的元素b
                if(j==lo)
                    break;
            if(i>=j)//左右扫描指针相等或左指针跑到右指针前面，说明扫描结束
                break;
            swap(arr,i,j);//交换前面找到的a b

        }
        swap(arr,lo,j);//最后交换切分元素，将切分元素放到指定的位置
        return j;
    }
 public static void swap(int arr[],int i,int j)
    {
        int temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
    }
 public static void main(String[] args) {
	 int[] arr= {2,3,1,7,6,5,8,0,9,4};
	 quickSort(arr, 0, arr.length-1);
		System.out.println(Arrays.toString(arr));
}
}

当然你可以使用最后一个元素作为切分元素，将上面的 partition方法修改如下即可：

public static int partition(int arr[],int lo,int hi)
    {
        int i=lo-1;
        int j=hi;
        int v=arr[hi];//切分的元素
        while (true)
        {
            //保证切分元素左边的元素都比它小，右边的元素都比它大
            while (arr[++i]<v)//查找比切分元素大的元素a
                if(i==hi)
                    break;
            while (arr[--j]>v)//查找比切分元素小的元素b
                if(j==lo)
                    break;
            if(i>=j)//左右扫描指针相等或左指针跑到右指针前面，说明扫描结束
                break;
            swap(arr,i,j);//交换前面找到的a b

        }
        swap(arr,hi,i);//最后交换切分元素，将切分元素放到指定的位置
        return i;
    }

4. 插入排序

4.1 直接插入排序

思想：对于一个有序序列，从尾部再加入一个数字，使得这个序列依然有序

n个数据需要n-1趟插入操作
每次插入完成保证数组开始到插入位置的区间内元素有序
时间复杂度：平均： $O(n^2) \quad$ 最坏： $O(n^2) \quad$ 最好： $O (n)$ （数组已经有序，每趟只需要比较1次就退出当前趟的比较）
空间复杂度：O(1）
稳定排序

package datastructure.sort;

import java.util.Arrays;

public class DirectInsertSort {
	public static void sort(int[] arr) {
		int n=arr.length;
		//i=0 j=1 插入第2个元素
		//i=1 j=2 插入第3个元素
		//i=n-2 j=n-1  插入最后一个元素
		//第i趟插入，将第i个元素插入到区间[0,i-1]元素序列中
		for(int i=1;i<=n-1;i++) {
			for(int j=i;j>0;j--) {
				if(arr[j]<arr[j-1]) {//后面的小于前面的
					int tmp=arr[j];
					arr[j]=arr[j-1];
					arr[j-1]=tmp;
				}else {//否则说明已经前面这部分有序了
					break;
				}
			}
		}
	}
	public static void main(String[] args) {
		int[] arr= {21,30,49,30,16,9};
		sort(arr);
		System.out.println(Arrays.toString(arr));
	}
}

4.2 折半插入排序

折半插入排序是对直接插入排序的一种优化，当插入第i个元素时，区间[0,i-1]内的元素其实已经有序，就不需要一个一个地去找元素i应该插入的位置，可以利用二分查找

package datastructure.sort;

import java.util.Arrays;

public class BinaryInsertSort {
	public static void sort(int[] arr) {
		int n=arr.length;
		//i=0 j=1 插入第2个元素
		//i=1 j=2 插入第3个元素
		//i=n-2 j=n-1  插入最后一个元素
		//第i趟插入，将第i个元素插入到区间[0,i-1]元素序列中
		for(int i=1;i<=n-1;i++) {
			int left=0,right=i-1;
			while(left<=right) {
				int mid=left+(right-left)/2;
				//待插入元素arr[i]大于中间元素 arr[i]在中间元素的右边
				if(arr[i]>=arr[mid])//这里取大于等于 即使30 30这种情况 后面的30不会插入到前面 保证稳定性
					left=mid+1;
				else {//待插入元素arr[i]小于中间元素 arr[i]在中间元素的左边
					right=mid-1;
				}
			}
			
			int tmp=arr[i];
			for(int j=i;j>left;j--) {//[left+1,i-1]元素后移
				arr[j]=arr[j-1];
			}
			arr[left]=tmp;//待插入元素arr[i]的位置是left left的含义：比arr[i]小的元素个数
		}
	}
	public static void main(String[] args) {
		int[] arr= {21,30,18,49,30,16,9};
		sort(arr);
		System.out.println(Arrays.toString(arr));
	}
}

4.3 希尔排序

希尔排序是堆直接插入排序的一种改进，加大了插入排序元素中的间隔，并在这些有间隔的元素间进行插入排序，从而使得数据项大跨度地移动

一个例子：9 -16 21* 23 -30 -49 21 30* 30
在这里插入图片描述

当步长h为4时：
9和30形成有序
-16和-49形成有序
21和21形成有序
30和23形成有序
30 2 -30 形成有序

package datastructure.sort;

import java.util.Arrays;

public class ShellSort {
	public static void sort(int[] arr) {
		int n=arr.length;
		int h=1;
		while(h<n/3) {
			h=3*h+1;//1 4 13 40.....
		}
		while(h>=1) {
			//将数组变为h有序  arr[i]  arr[i+h] arr[i+2h]...有序
			for(int i=h;i<n;i++) {
				System.out.println("i="+i);
				for(int j=i;j>=h;j-=h) {
					System.out.println("j:"+j+"  j-h:"+(j-h));
					if(arr[j]<arr[j-h]) {//后面的比前面小
						int tmp=arr[j];
						arr[j]=arr[j-h];
						arr[j-h]=tmp;
					}
					else {
						break;
					}
				}
			}
			System.out.println("---------------------------");
			h/=3;
		}
			
	}
	public static void main(String[] args) {
		int[] arr= {9 ,-16 , 21, 23 ,-30 ,-49, 21 ,30, 30};
		sort(arr);
		System.out.println(Arrays.toString(arr));
	}
}

为了形象地打印过程，去掉else语句块中的break:
打印如下：
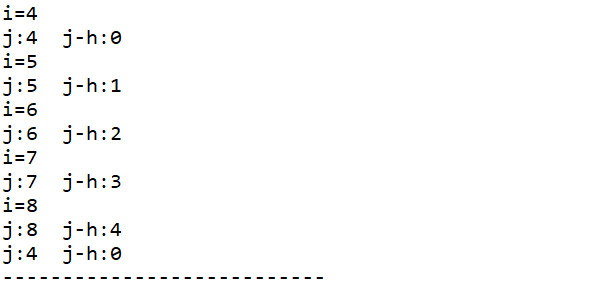
在这里插入图片描述

在这里插入图片描述

5. 归并排序

两个关键步骤：划分和合并
需要用一个临时数组来保存合并两个有序序列后的新序列
时间复杂度: 最好 $\quad$ 最坏 $\quad$ 平均 $\quad$
空间复杂度：最好： $\quad$ 最坏： $\quad$
合并部分，也就是merge部分，代码实现类似于将两个有序数组合并的代码，首先是合并只有1个元素的两个数组，然后合并有两个元素的有序数组，，合并有4个元素的有序数组…
稳定排序

package datastructure.sort;

import java.util.Arrays;

public class MergeSort {
	public static void merge(int arr[],int temp[],int lo,int mid,int hi)
    {
        int i=lo;
        int j=mid+1;
        int t=0;
        while (i<=mid&&j<=hi)
        {
            if(arr[i]<arr[j])//如果左边的有序序列的当前元素小于右边有序序列的当前元素
                temp[t++]=arr[i++];
            else//如果左边的有序序列的当前元素大于右边有序序列的当前元素
                temp[t++]=arr[j++];
        }
        while (i<=mid)//左半边元素未用尽
            temp[t++]=arr[i++];
        while (j<=hi)//右半边元素未用尽
            temp[t++]=arr[j++];

        t=0;
        int k=lo;
        while (k<=hi)//将两个有序序列合并在一起的temp数组重新赋值给arr数组
            arr[k++]=temp[t++];

    }
    public static void mergeSort(int arr[],int temp[],int lo,int hi)
    {
        if(hi<=lo)
            return;
        int mid=(lo+hi)/2;
        mergeSort(arr,temp,lo,mid);//对左半部分进行排序
        mergeSort(arr,temp,mid+1,hi);//对右半部分进行排序
        merge(arr,temp,lo,mid,hi);//开始合并左半部分和右半部分
    }
    public static void main(String[] args) {
    	 int[] arr= {2,3,1,7,6,5,8,0,9,4};
    	 int[] tmp=new int[arr.length];
    	 mergeSort(arr, tmp,0, arr.length-1);
    		System.out.println(Arrays.toString(arr));
	}

}

归并排序的详细解释：归并排序自顶向下和自底向上分析及实现

下面介绍的是线程时间复杂度排序，这种线性复杂度是用空间换的，即用空间换时间

6. 计数排序

一个简答的例子：对一个班的考试成绩进行排名，一种做法就是统计处各个分数的人数，然后再累加
比如<=70的有25人，择71分排在位置26，简单来说，如果有10个元素小于X，则X的位置应该是11

计数排序假设元素>=0, 并且知道一个最大值的范围，假设最大值为K
需要一个大小为K+1的数组C来计数
需要一个大小为n的数组B来存放排序后的数据(n为元素个数)

package datastructure.sort;

import java.util.Arrays;

public class CountingSort {
	public static void sort(int[] arr) {
		
		int maxNum=Arrays.stream(arr).max().getAsInt();
		int n=arr.length;
		int[] C=new int[maxNum+1];
		int[] B=new int[n];
		for(int num:arr) {
			C[num]++;//统计每个元素出现的次数
		}
		for(int i=1;i<=maxNum;i++) {
			C[i]+=C[i-1];//C[i]表示<=i的元素的个数
		}
		System.out.println(Arrays.toString(C));
		//这里从后往前处理是因为 对于5 5 5这种情况 先处理到后面的5 放到较后面的位置 保证稳定性
		for(int i=n-1;i>=0;i--) {
			int num=arr[i];
			int cnt=C[num];//<=arr[i]的有cnt个
			B[cnt-1]=num;//第cnt个位置（索引是cnt-1）放置arr[i]
			C[num]-=1;//arr[i]待处理的数量减一  如果有多个的arr[i]的话 将会往前面放
		}
		System.out.println(Arrays.toString(B));
		
	}
	public static void main(String[] args) {
//		int[] arr= {2,3,1,7,6,5,8,0,9,4};
		int[] arr= {1,1,1,3,5,6,9,8,9,9,6,5,2,4,0};
		sort(arr);
		
	}
}

7. 桶排序

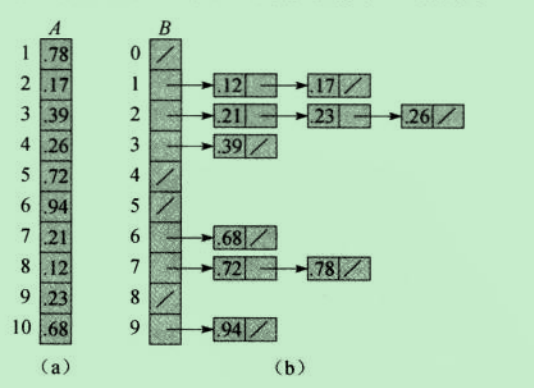
在这里插入图片描述

假设需要排序的元素：0.12 0.17 0.21 0.23 0.26 0.39 0.68 0.72 0.78 0.94
先创建一个大小为10的桶，每个桶中将映射到桶中的元素以链表的形式存放（类似于HashMap），然后对每个桶中的元素进行排序，排完序之后按顺序各个链表中的元素加入原数组中的即可

package datastructure.sort;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Random;

public class BucketSort {
	public static final int BUCKETS=10;
	public static void sort(double[] arr) {
		ArrayList<Double>[] buckets=new ArrayList[BUCKETS];
		for(int i=0;i<BUCKETS;i++) {
			buckets[i]=new ArrayList<>();
		}
		int n=arr.length;
		
		for(int i=0;i<n;i++) {
			int val=(int) (10*arr[i]);
			buckets[val].add(arr[i]);//将元素加入对应的桶中
		}
		for(int i=0;i<BUCKETS;i++) {
			Collections.sort(buckets[i]);//对桶中的链表进行排序
		}
		int index=0;
		for(int i=0;i<BUCKETS;i++) {
			System.out.println(buckets[i]);
			for(int j=0;j<buckets[i].size();j++) {
				arr[index++]=buckets[i].get(j);//第i号桶中的第j个元素
			}
		}
		
	}
	public static void main(String[] args) {
		int N=20;
		Random random=new Random();
		double[] arr=new double[N];
		for(int i=0;i<N;i++) {
			arr[i]=random.nextDouble();
		}
		System.out.println("排序前："+Arrays.toString(arr));
		sort(arr);
		System.out.println("排序后:"+Arrays.toString(arr));
	}
	
}

分析：假设有n个元素，有m个桶，元素平均分布在每个桶中，即每个桶中的元素个数是n/m, 则对每个桶中的元素进行快速排序，时间复杂度是 $\frac{n}{m} \times log\frac{n}{m}$ , 一共有m个桶，所以总的复杂度是： $m\times\frac{n}{m} \times log\frac{n}{m}=nlog\frac{n}{m}$
当桶的个数m足够多，比如等于n时， $nlog\frac{n}{m}=n$ , 这是最好的情况
如果极端情况n个元素落在一个桶中，则时间复杂度是 $n l o g n$

在桶排序中，对于每个桶中的元素不仅仅可以采用快速排序，也可以使用计数排序

8. 基数排序

思想：

取每个元素的最低位
基于最低位对元素进行排序
对下一个最低位重复上述过程

用于处理数组元素是整数的情况，如果需要处理负数需要作相应处理

在这里插入图片描述

package datastructure.sort;

import java.util.Arrays;

public class RadixSort {
	public static void radixSort(int arr[])
    {
        //先求出数组元素中最大数的位数
        int max=Arrays.stream(arr).max().getAsInt();
       
        int maxLength=(max+"").length();//最大数字的位数,转化为字符串求长度比较简单

        int bucket[][]=new int[10][arr.length];//创建10个桶，每个桶的大小是原数组中元素的个数
       //第一维是表示数字0-9  第二维是表示相应基数的元素的个数 0号桶到9号桶
        int[] bucketElementCounts = new int[10];//记录每个桶中放的元素的个数  
        //bucketElementCounts[0]的数值就是0号桶中元素的个数 依次类推

        for(int i=0,n=1;i<maxLength;i++,n*=10)//最大数字的位数几位决定了需要进行几次排序
        {
            for(int j=0;j<arr.length;j++)
            {
                int num=arr[j]/n%10;//获取当前位置的数字
                //n=1时获取个位数字   n=10时获取十位数字....
                int cnt=bucketElementCounts[num];//当前取余后的数字的num的元素个数
                bucket[num][cnt]=arr[j];//将对应位置的数字放进对应的桶中
                bucketElementCounts[num]++;//余数为num的元素个数+1
            }

            int index=0;

            for(int j=0;j<bucketElementCounts.length;j++)
            {
                if(bucketElementCounts[j]!=0)//当前j号桶中有元素
                {
                    for(int k=0;k<bucketElementCounts[j];k++)
                        arr[index++]=bucket[j][k];//将j号桶中的k号元素重新放入原数组中

                }
                bucketElementCounts[j]=0;//清空j号桶
            }
            System.out.println(Arrays.toString(arr));
   
        }

    }
	public static void main(String[] args) {
		int[] arr= {329,457,657,839,436,720,355};
		radixSort(arr);
	}
}