这类问题需要注意三个问题
1、存储问题:一般用二维数组存储
2、枚举对象:一般以坐标作为枚举对象
3、坐标增量:二维数组或者两个一维数组
迷宫问题
先看一个简易迷宫问题吧
现在有一个小迷宫,如图所示,请编程求解从入口到终点的最短路径。
迷宫由n行m列的单元格组成,且n,m小于等于50.注意黑色区域快不可以走,只能走白色区域。
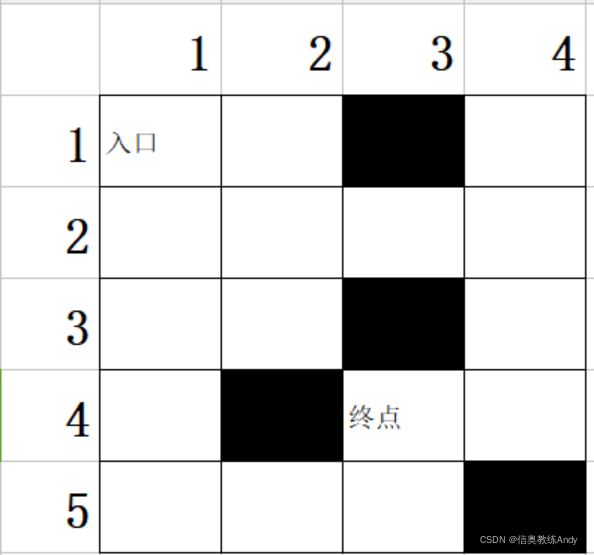
输入: 第一行:n,m,分别代表n行m列。
第2-n行表示为迷宫,0表示空地,1表示障碍物。
最后一行,x,y,p,q前两个为入口坐标,后两个为终点坐标。 输出: 最短路径样例输入:
5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3
样例输出;
7
【分析问题】
一、分析题意:
从入口可以向右和向下走,一次遍历所有的路径,找出可以走的路径,记录可以到达终点的路径,并打擂台的形式找出最短路径。
二、算法分析
1、规定一个走的顺序,按照顺时针的方向来尝试,即按照右、下、左、上的顺序去尝试所有路径。
2、用深搜来实现这个方法。那么dfs()函数如何写呢?
dfs()的功能是解决当前应该怎么办;
1)检查是否已经到终点(比较容易实现吧)
dfs()只需要维护三个参数,分别为当前这个点的坐标x,y以及当前已经走过的步数step
void dfs(int x,int y,step)
{
if(x==p&&y==q)//判断是否到达终点
{
if(step<min)//打擂台更新最小值
min=step;
return;//注意这里的返回很重要哦。
}
}
2)如果没有到达终点,找出下一步可以走的地方。
用一个方向数组next[4][2]来定义四个方向。
int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
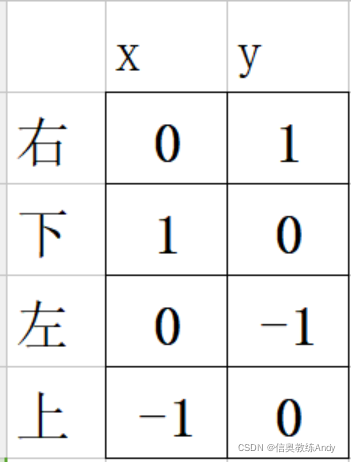
通过这个方向数组,使用循环就很容易获得下一步的坐标,这里用tx,ty存储坐标。
for(int k=0;k<=3;k++)
{
tx=x+next[k][0];
ty=y+next[k][1];
}
为了避免重复访问一个点,需要用book[tx][ty]来记录(tx,ty)是否已经在路径中。
如果这个点符合所有的要求,就对这个点进行下一步的扩展,即dfs(tx,ty,step+1)。
代码如下:
for(int k=0;k<=3;k++)
{
tx=x+next[k][0];
ty=y+next[k][1];
//判断是否越界
if(tx<1||tx>n||ty<1||ty>m)
continue;
//判断该点是否可走或者是否在路径中
if(a[tx][ty]==0&&book[tx][ty]==0)
{
book[tx][ty]=1;
dfs(tx,ty,step+1);
book[tx][ty]=0;//回溯
}
来看一下完整代码吧
#include<iostream>
using namespace std;
int n,m,p,q,minn=9999;
int a[51][51],book[51][51];
void dfs(int x,int y,int step)
{
int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
//通过这个方向数组,使用循环就很容易获得下一步的坐标,这里用tx,ty存储坐标。
int tx,ty,k;
if(x==p&&y==q)//判断是否到达终点
{
if(step<minn)//打擂台更新最小值
minn=step;
return;//注意这里的返回很重要哦。
}
//枚举4种走法
for(int k=0;k<=3;k++)
{
//计算下一个点的坐标
tx=x+next[k][0];
ty=y+next[k][1];
//判断是否越界
if(tx<1||tx>n||ty<1||ty>m)
continue;
//判断该点是否可走或者是否在路径中
if(a[tx][ty]==0&&book[tx][ty]==0)
{
book[tx][ty]=1;
dfs(tx,ty,step+1);
book[tx][ty]=0;//回溯
}
}
return;
}
int main()
{
int i,j,sx,sy;
cin>>n>>m;
//读入迷宫
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
cin>>a[i][j];
//读入起点和终点坐标
cin>>sx>>sy>>p>>q;
//从起点开始搜索,将起点纳入路径中
book[sx][sy]=1;
dfs(sx,sy,0);
cout<<minn;
return 0;
}
八皇后问题
【问题解析】
1、枚举对象当然是8个皇后了,但是要求同行、同列、同对角线不能冲突,因此,我们枚举每一行的皇后放置,这样只需要判断同列、同对角线即可。

2、同对角线的判定

黑色表示主对角线(x-y+n),红色表示副对角线(x+y)


【参考代码】
#include<bits/stdc++.h>
using namespace std;
#define maxn 100
int a[maxn],b1[maxn],b2[maxn],b3[maxn];//分别记录x,x+y,x-y+15是否被占用
int n ,ans = 0;
void dfs(int x)
{
if(x>n)
{
ans++;
if(ans<=3)
{
for(int i = 1;i <= n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
}
return ;
}
for(int i = 1;i<=n;i++)
{
if(b1[i]==0 && b2[x+i]==0 && b3[x-i+15]==0)
{
a[x]=i;
b1[i]=1;
b2[x+i]=1;
b3[x-i+15]=1;
dfs(x+1);
b1[i]=0;
b2[x+i]=0;
b3[x-i+15]=0;
}
}
}
int main()
{
cin>>n;
dfs(1);
cout<<ans;
}
数独问题
简化问题,我们先来看四阶数独。
1、枚举对象:我们来填空,每个空都填完,枚举结束

2、判定同行,同列,同方格是否重复

#include<bits/stdc++.h>
using namespace std;
#define size 5
int a[size*size],n= 4*4,ans = 0;
int b1[size][5],b2[size][5],b3[size][5];//分别记录 横行、竖行、四小块
void dfs(int x)//第x个空填什么
{
if(x>n)
{
ans++;//统计方案数
for(int i = 1;i<=n;i++)//输出方案
{
cout<<a[i]<<" ";
if(i%4==0) cout<<endl;
}
cout<<endl;
return ;
}
int row = (x-1)/4+1;
int col = (x-1)%4+1;
int block = (row-1)/2*2+(col-1)/2+1;
for(int i = 1;i<=4;i++)
{
if(b1[row][i]==0&&b2[col][i]==0&&b3[block][i]==0)
{
a[x]=i;
b1[row][i]=1;
b2[col][i]=1;
b3[block][i]=1;
dfs(x+1);
b1[row][i]=0;
b2[col][i]=0;
b3[block][i]=0;
}
}
}
int main()
{
dfs(1);
cout<<ans;
return 0;
}
临时抱佛脚
【题解】从这些题目中取其中一部分作为一个子集,使这些题目总耗时不超过这个科目的总耗时的一半,但是尽可能大。这样就可以将这个科目的题目分为尽可能均等的两部分了。
可以借鉴之前讲过的枚举子集—每个题目放入或者不放入子集中。
#include<bits/stdc++.h>
using namespace std;
int nowt,maxt,sum;
int ans,maxdeep;//最深递归层数(作业数量)
int s[4],a[21];
void dfs(int x)
{
if(x > maxdeep)//所有作业枚举完毕,达到了最大递归层数
{
maxt = max(maxt,nowt);
return ;
}
if(nowt +a[x]<=sum/2)
{
nowt += a[x];
dfs(x+1);//下一层递归
nowt-=a[x];
}
dfs(x+1);//不选这科
}
int main()
{
cin>>s[0]>>s[1]>>s[2]>>s[3];
for(int i = 0;i<4;i++)
{
nowt = 0;
maxdeep = s[i];
sum = 0;//别忘了每次换科都要初始化
for(int j = 1;j<=s[i];j++)
{
cin>>a[j];
sum+=a[j];//记录这科总耗时
}
maxt = 0;
dfs(1);
ans += (sum-maxt);//加上答案
}
cout<<ans;
}
