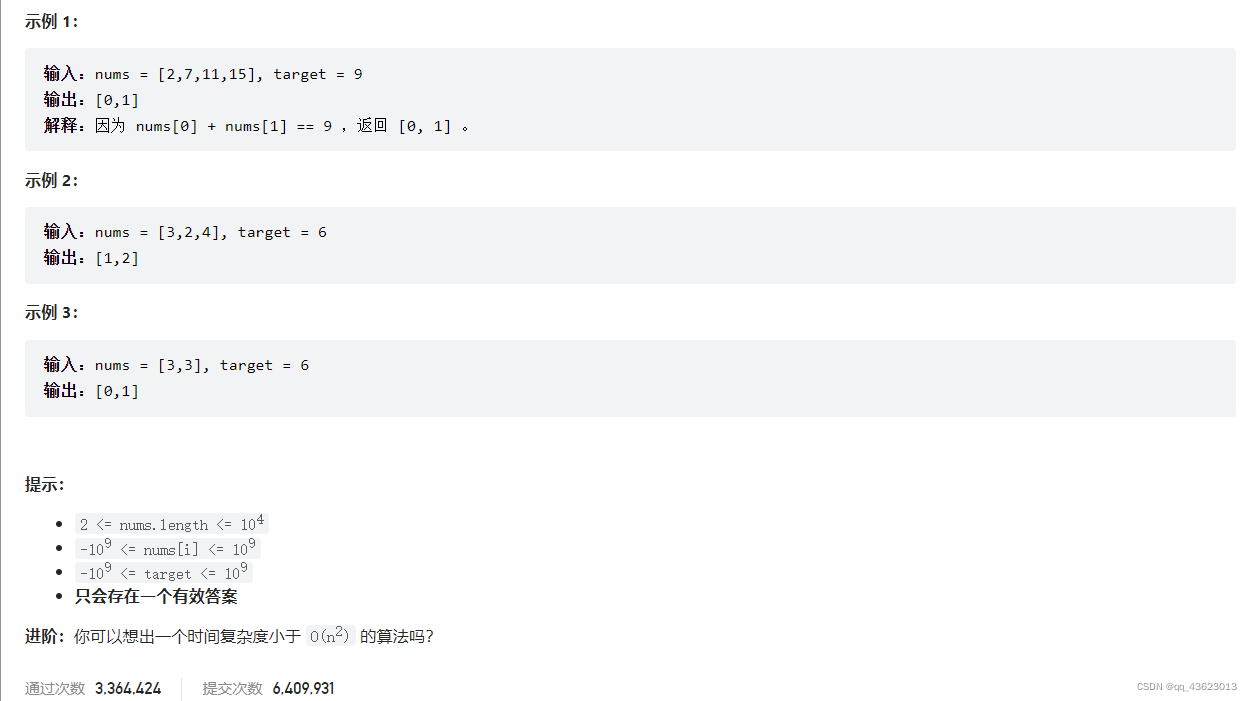
题目要求
1、给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
2、你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
3、你可以按任意顺序返回答案。
方法一:两次for循环遍历
class Solution {
//暴力方式,直接遍历
//时间复杂度:O(N^2),N是数组中元素的数量,最坏的情况下数组中任意两个数都要被匹配一次。
//控件复杂度:O(1) 只用到常数个临时变量
public int[] twoSum(int[] nums, int target) {
int [] result = new int[2];
for (int i = 0; i < nums.length; i++) {
for (int j = i+1; j < nums.length; j++) {
if (target == (nums[i]+nums[j])){
result[0] = i;
result[1] = j;
return result;
}
}
}
return null;
}
}
结果不用说,使用这种方式,执行用时长,内存消耗大(真是离 高效率,高性能越来越远了)

方法二:查找表法(官方的讲解)
在遍历的同时,记录一些信息,以省去一层循环,用“空间换时间”。
需要记录已经遍历过的数值和它所对应的下标,可以借助查找表实现
查找表两种常用的实现:
哈希表(因为不考虑顺序,因此用哈希表实现)
平衡二叉搜索树(暂时不懂,需要先研究研究)
class Solution {
//使用哈希表
public int[] twoSum(int[] nums, int target) {
//存放的类型为两个int值,初始化容量
Map<Integer,Integer> map = new HashMap(nums.length-1);
//数组中的第一个数字一定会存入map中
map.put(nums[0],0);
for (int i = 1; i < nums.length; i++) {
//判断当前map中的key值中是否存在 所希望获取的结果值(目标值-当前遍历的值的插值)
if (map.containsKey(target-nums[i])){
return new int[]{map.get(target-nums[i]),i};
}
map.put(nums[i],i);
}
return null;
}
}
从结果来看,通过哈希表的方式,效率提升了

复杂度分析(复杂度还不太懂,需要进一步学习呀)
时间复杂度:O(N),其中 N 是数组中的元素数量。对于每一个元素 x,我们可以 O(1) 地寻找 target - x。
空间复杂度:O(N),其中 N 是数组中的元素数量。主要为哈希表的开销。
