食用指南：

对该算法程序编写以及踩坑点很熟悉的同学可以直接跳转到代码模板查看完整代码
只有基础算法的题目会有关于该算法的原理，实现步骤，代码注意点，代码模板，代码误区的讲解
非基础算法的题目只有题目分析，代码实现，代码误区

题目描述：

给定你一个长度为 n 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式
输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在 1～109 范围内），表示整个数列。

输出格式
输出共一行，包含 n 个整数，表示排好序的数列。

数据范围
1≤n≤100000
题目来源：https://www.acwing.com/problem/content/789/

题目分析：

没有什么好分析的了，归并排序

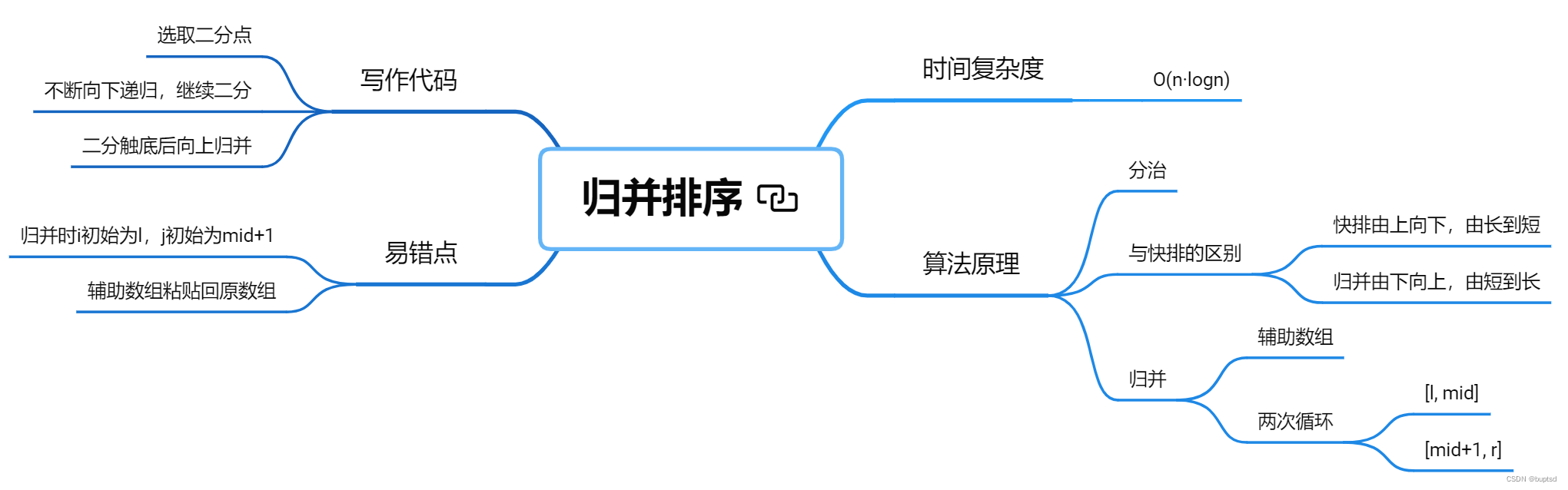
算法原理：

基于分治

将序列划分为左右两个区间，再将左右区间继续划分，直到不能继续划分为止；
将相邻的两个小区间有序合并为一个大区间，直到合并回原本的序列
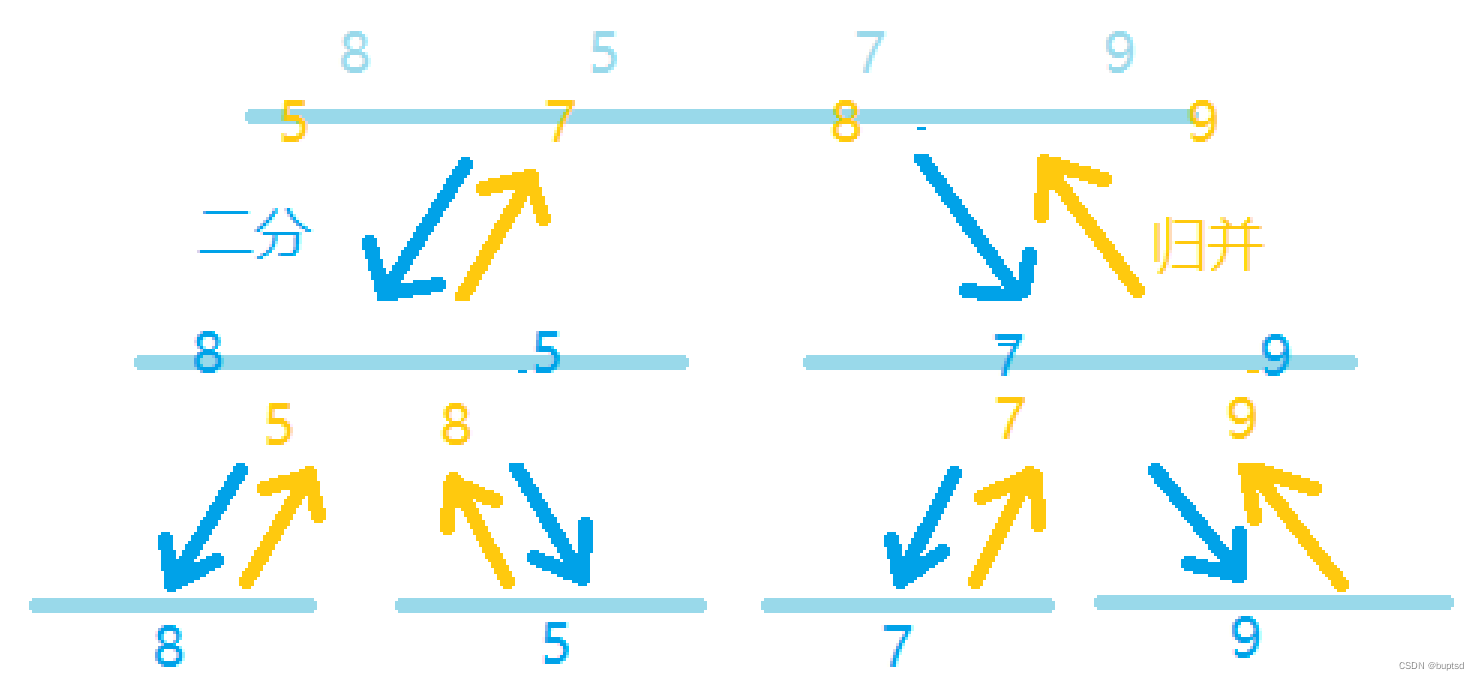
归并：两个小区间有序合并为一个大区间称为归并

和快速排序的区别

快排：
先做到安置好基准点位置和左右区间相对有序
再递归进入左右区间
归并：
先递归进入左右区间
再将左右区间有序合并为一个大区间
总结：
快排自上向下，归并自下向上
快排由长到短，归并由短到长

时间复杂度：

O(n·logn)，同于快速排序，都比C++内置的sort()速度略快
递归状态树深度：
每次将一段区间二分，共二分了logn次，状态树也是logn层
状态树每层：
归并时，每层的一个节点序列由遍历下一层的两个子序列合并而来；
一层的所有节点代表的子序列之和就是原序列长度；
每一层都是遍历上一层所有子序列合并而来，时间复杂度都是n

写作步骤：

三步走

粗暴二分作为分界点，mid = (l+r)>>1;
左右区间继续递归二分
将小的左右区间有序归并为大区间

🌟最难的步骤在第3步：有序归并
🌟关键步骤也在第3步：做到了左右区间有序合并

核心算法：

有序归并：

双指针算法：

i指针指向左序列arr[m]
j指针指向右序列arr[n]
创建新序列，长度为m+n
比较arr[i] 和 arr[j]每次将较小的或等大的放入新序列中，放入新序列后该指针++，否则保持不变
当一个序列被指针遍历结束，而另一个还未结束，则将剩余部分全加入新序列中

代码注意：

先创建辅助合并数组tmp[10000]
由于递归处理左右区间，所以函数需要携带区间边界l,r参数
递归终止条件：l >=r
先递归到最底层，回溯时才合并左右子序列
i,j指针分别负责合并左右区间，不可以越界，
有一方全部并入后令一方剩余部分才全部并入
合并好的有序序列需要复制回原数组
二分的序列区间不可重复，一般这点写不错

代码模板：

#include <iostream>
using namespace std;
const int N = 100010;
int arr[N];
//加速点1：事先预备好归并辅助数组tmp
int tmp[N];
void merge_sort(int l, int r){
    if(l >= r) return;
    int mid = (l+r) >> 1;
    merge_sort(l,mid,arr);
    merge_sort(mid+1, r, arr);
    //注意点1：i从l到mid，j从mid+1到r
    int k = 0, i=l, j=mid+1;
    while(i<=mid && j<=r){
        if(arr[i] < arr[j]) tmp[k++] = arr[i++];
        else tmp[k++] = arr[j++];
    }
    while(i<=mid) tmp[k++ ]= arr[i++];
    while(j<=r) tmp[k++]  =arr[j++];
    //注意点2：归并结果需要从辅助数组tmp转移到原数组
    for(int i=l, j=0; i<=r; i++, j++){
        arr[i] = tmp[j];
    }
}
int main(){
    int n = 0;
    cin >> n;
    for(int i=0; i<n;i++){
        cin >> arr[i];
    }
    merge_sort(0,n-1);
    for(int i=0; i<n; i++){
        cout << arr[i]<<" ";
    }
}