D

点击此处查看对应的题目.
本题设计算法：逆元 + 快速幂 + 二次函数性质
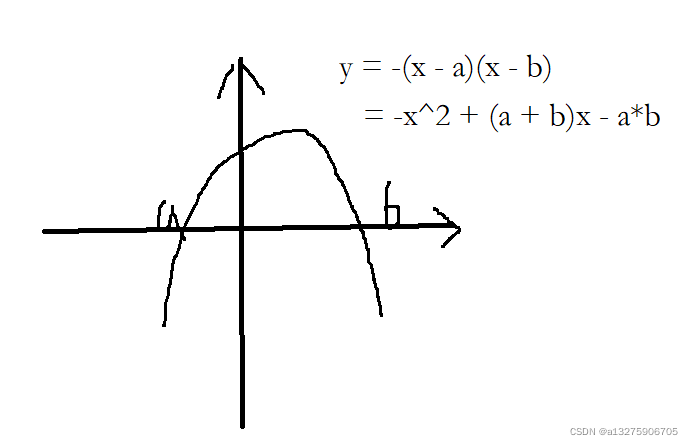
请添加图片描述

本题要求得到两和之差的最大值：由图像可知，S(b) - S(a - 1) 即为f(x) 的最大值（类似前缀和）。

所以这里我们要求得S(a) 和 S(b)，所以，我们要得到求 S 的公式

$S (x)$ = $-\displaystyle \sum_{1}^{x}x^2 + (a + b)\displaystyle \sum_{1}^{x}x +(a * b)\displaystyle \sum_{1}^{x}1$

分别求和

$\displaystyle \sum_{1}^{x}x^2$ ：数学归纳法：
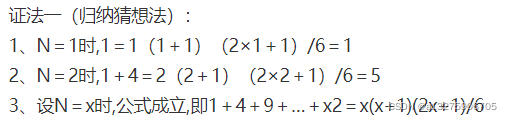
$\displaystyle \sum_{1}^{x}x$ ：等差数列求和
$\displaystyle \sum_{1}^{x}1$ ：即为 n

最后还需要注意一点：
由于本题需要对答案取模运算，且本题目的求和公式中包含除法取模操作，所以，不能直接取模，被除数直接乘上除数的乘法逆元即可与之等效。

求乘法逆元：由于本题的 mod 值是质数，所以我们可以用快速幂求逆元的方法求出乘法逆元

时间复杂度 $O (l o g n)$

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll N = 1e5 + 10,mod = 998244353;

ll qmi(ll a,ll b) 
{
    ll res = 1;
    while (b) {
        if (b & 1) res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}
ll S(ll n,ll a,ll b)
{
    ll x = n * (n + 1ll) % mod * (2ll * n + 1ll) % mod * qmi(6,mod - 2) % mod;
    ll y = (a + b) * n % mod * (n + 1ll) % mod * qmi(2,mod - 2) % mod;
    ll z = a * b % mod * n % mod;
    ll res = (-x + y - z) % mod;
    res = (res + mod) % mod;
    return res;
}
int main()
{
    int t;
    cin >> t;
    while (t -- ) {
        ll a,b;
        cin >> a >> b;
        cout << (S(b,a,b) - S(a - 1,a,b) + mod) % mod << '\n';
    }
    return 0; 
}

E

点击此处查看对应的题目.
本题设计算法：递推 / 思维DP?

本题主要需要通过对比可能的数据，我们可以发现一下特点

每次走一步都必须比原来的数字+1
dp[i] = dp[i - 1]/dp[i + 1] - a[i] 的规律（dp[i]表示从第 i 个点开始的最小初始值）

对比数据:
1 2 3 4 0
2 2 1 10 0
2 1 0 1 2

时间复杂度 $O (n)$

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const ll N = 3e6 + 10,INF = 1e18;
ll a[N],dp[N];//dp[i]表示从第 i 个点开始的最小初始值

void solve()
{
    int n,idx;
    cin >> n;
    for (int i = 1;i <= n;i ++ ) {
        scanf("%lld",&a[i]);
        if (!a[i]) idx = i;
    }
    if (n == 1) {
        puts("No Solution");
        return;
    }
    for (int i = 1;i <= n + 5;i ++ ) dp[i] = INF; 
    for (int i = idx - 1;i >= 1; i -- ) {
        dp[i] = a[i] + 1;
        if (i != idx - 1) dp[i] = max(dp[i],dp[i + 1] - a[i]);
    }
    for (int i = idx + 1;i <= n;i ++ ) {
        dp[i] = a[i] + 1;
        if (i != idx + 1) dp[i] = max(dp[i],dp[i - 1] - a[i]);
    }
    ll res = INF;
    for (int i = 1;i <= n;i ++ ) res = min(res,dp[i]);
    cout << res << '\n';
}
int main()
{
    int t;
    cin >> t;
    while (t -- ) solve();
    return 0;
}