首先看状态dfs,题目是检查是否有合法括号字符串

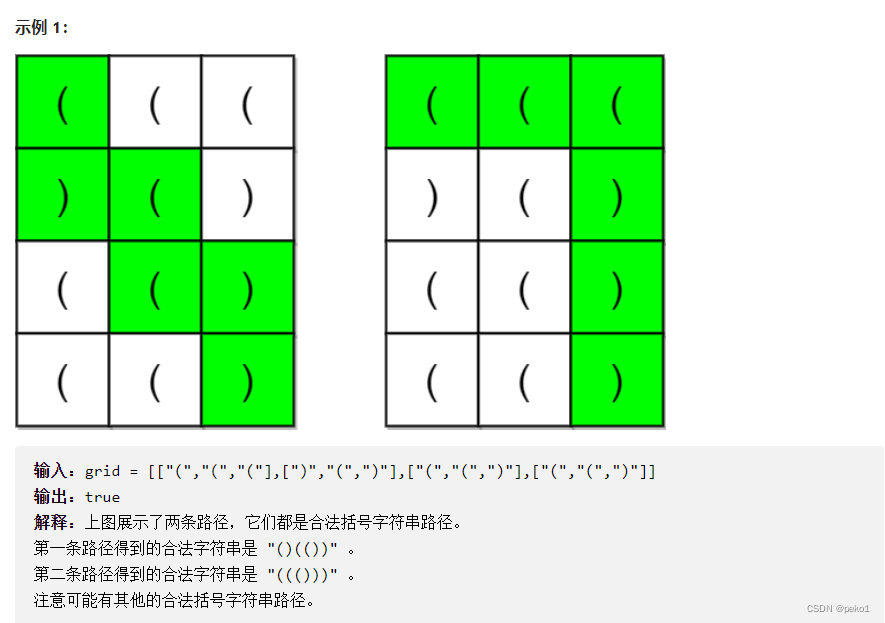
- 用c表示字符串的状态(平衡度):遇到左括号就+1,遇到右括号就-1,那么合法的字符串即为任意时刻 c ≥ 0 c≥0 c≥0且最后c=0
- 从左上角到右下角,往右走m-1次,往下走n-1次因此路径长度是固定的,为(m-1)+(n-1)+1=m+n-1;极限的情况下左半边全为左括号,右半边全为右括号,因此c的最大值为(m+n-1)/2
- 当遍历到(x,y)结点时,后面还剩下(m-1-x)+(n–1-y)+1=m-x+n-y-1,如果此时c大于这个值,后面就算全为右括号也不能使其变成0,直接返回false
- 由于访问到最终结点后会直接返回,因此如果访问到已经访问过的结点,说明这个结点的这个状态是不能到达最终结点的最终状态的,可以直接返回false
- 每次遍历之后更新c的值,直到访问到最终结点时c的值为1,说明找到了一条合法路径
代码如下:
int vis[105][105][105];
bool dfs(vector<vector<char>>& grid,int x,int y,int c){
int m=grid.size();
int n=grid[0].size();
if(x==m-1&&y==n-1) return c==1; //访问到了右下角结点,判断c是否等于1
if(c>m-x+n-y-2+1) return false; //剪枝,判断此节点能否合法的到达最终结点
if(vis[x][y][c]) return false; //已经访问过的结点直接返回false
vis[x][y][c]=1;
if(grid[x][y]==')') c--; //更新c的值
else c++;
if(c<0) return false; //如果c小于0了直接返回false
return (x<m-1&&dfs(grid,x+1,y,c))||(y<n-1&&dfs(grid,x,y+1,c)); //继续向右和下搜索
}
bool hasValidPath(vector<vector<char>>& grid) {
int m=grid.size();
int n=grid[0].size();
if(grid[0][0]==')'||grid[m-1][n-1]=='(') return false;
return dfs(grid,0,0,0);
}
状态bfs题目如下网格中的最短路径

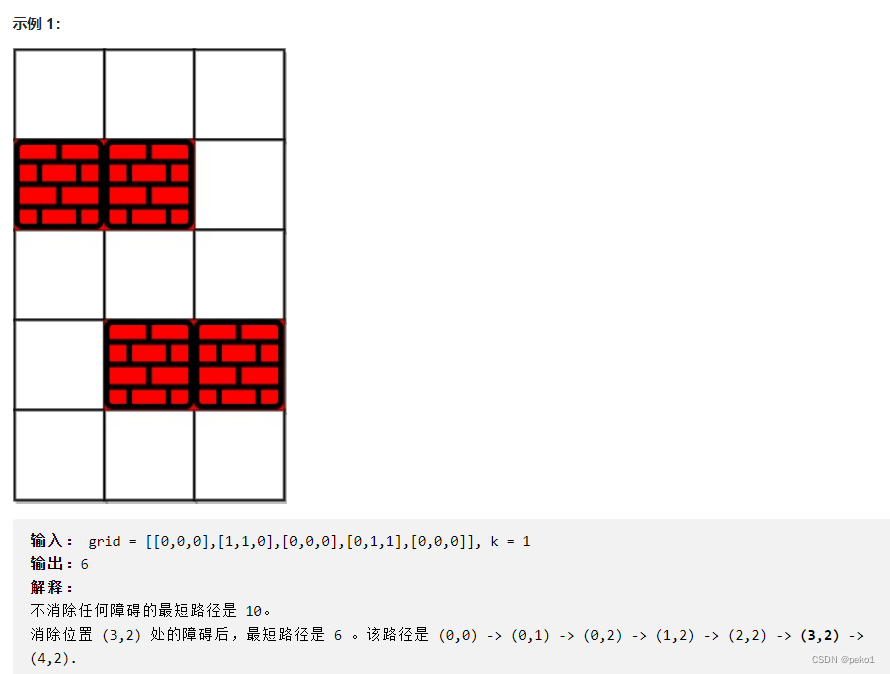
- 对于二维网格中的最短路问题,可以采用广度优先搜索的方法解决
- 除了记录当前位置x,y,我们还记录还能消除障碍物的数量k,用三元组(x,y,rest)表示,对于当前状态,我们最多向四个方向进行搜索,设新的位置为(dx,dy),如果该位置为障碍物,新的三元组为(dx,dy,rest-1),否则为(dx,dy,rest),rest小于0的情况我们就不用去考虑,直接移除队列中
- 由于广度优先搜索的特性,当我们第一次遍历到右下角且rest大于等于0的时候,说明我们就找到了一条最短的路径,返回记录的路径长度即可
- 剪枝优化:我们可以发现从左上角到右下角的最短路中,最多只有(m+n-3)个障碍,且此最短路长度为(m+n-2),因此如果给定的k大于等于(m+n-3)的话,直接返回路径长度即可
代码如下:
int vis[45][45][90];
vector<vector<int>>dir={{-1,0},{1,0},{0,-1},{0,1}};
int shortestPath(vector<vector<int>>& grid, int k) {
int m=grid.size();
int n=grid[0].size();
if(m==1&&n==1) return 0;
queue<tuple<int,int,int>>q;
q.emplace(0,0,k);
if(k>=m+n-3) return m+n-2; //如果k大于此值的话,直接返回最短的路径
vis[0][0][k]=1;
int ans=0; //记录最短路径的长度
while(q.size()>0){
ans++;
int len=q.size();
for(int i=0;i<len;i++){
auto [first,second,third]=q.front();
q.pop();
for(auto& d:dir){
int dx=first+d[0];
int dy=second+d[1];
if(dx>=0&&dy>=0&&dx<m&&dy<n){ //新的位置在二维数组中,是否为障碍分开考虑
if(grid[dx][dy]==0&&!vis[dx][dy][third]){
if(dx==m-1&&dy==n-1) return ans; //到达终点返回路径长度
q.emplace(dx,dy,third);
vis[dx][dy][third]=1;
}
else if(grid[dx][dy]==1&&third-1>=0&&!vis[dx][dy][third-1]){
q.emplace(dx,dy,third-1);
vis[dx][dy][third-1]=1;
}
}
}
}
}
return -1;
}
