[数据结构与算法]量子计算 14 量子通用门

上回书学习了经典可逆通用门，主要是Toffoli/CCNOT门和Fredkin/CSWAP门，其中Toffoli/CCNOT门不仅可以实现所有的Boolean函数，还能实现所有的可逆或permutation操作；因为量子门都是可逆的，这两个门在量子里面同样适用。

1 经典门与量子门

经典门和量子门的区别在于其适用的操作对象，经典门在此仅讨论经典可逆门。

• 以两个比特为例，经典比特的可能状态为$00,01,10,11$四种，其实相当于一个只含$0$和$1$的单位向量，比如状态为00时，其向量为$[1,0,0,0{]}^{?}$，而一个经典可逆门，是将原来的四种状态与重新排列后的这四种状态的对应起来的变换，因此一个经典可逆门就是一个permutation矩阵，比如Toffoli/CCNOT和Fredkin/CSWAP门；而Fredkin/CSWAP的特点就是所对应的前后状态的1的数目一样，比如01只能对应10或01，而00和11只能保持不变。

• 而两个量子比特的状态是${\alpha }_0|00?+{\alpha }_1|01?+{\alpha }_2|10?+{\alpha }_3|11?$，其状态由四个量子幅组成的向量$[{\alpha }_0,{\alpha }_1,{\alpha }_2,{\alpha }_3{]}^{?}$来表示，当然经典门也可以应用在量子比特身上，作用效果就相当于将基的顺序变一下，比如原来是$|01?$的变换成了$|10?$；
  而体现在酉矩阵上，简单来说就不是permutation矩阵的酉矩阵，比如Hadamard门，Rotation gate $R_{\theta }$门，Phase shift $R_{?}$门；
  而一般的量子门也相当于把量子幅的基进行了变换，这对应与经典门只是把基重新排列了一下；
  因此经典门无法对量子叠加产生影响，因为改变量子叠加需要改变${\alpha }_1|0?+{\alpha }_2|1?$整体，而不是仅调换一下$|0?,|1?$的顺序。

2 量子通用门 Universal gates

定理: { CNOT , all?1-qubit?gates } \{\text{CNOT}, \text{all 1-qubit gates}\} {CNOT,all?1-qubit?gates} is universal

{ CNOT , all?1-qubit?gates } \{\text{CNOT}, \text{all 1-qubit gates}\} {CNOT,all?1-qubit?gates}是严格意义上的通用量子门，因为这个门集合可以产生所有的酉矩阵。

Proof sketch

证明简单介绍一下

• 任意一个酉矩阵都可以分解成$2\times 2$的旋转矩阵，这根据现代的givens rotation可以证明；
• 然后证明可以用Toffoli/CCNOT和任意1-qubit门表达givens rotation
• 然后证明CNOT和任意1-qubit门可以表达Toffoli/CCNOT门

3 近似通用门 (Approximate-universal gates)

严格意义上的通用门有个问题，所有的1-qubit门有不可数无穷多个，或者说有连续的无穷多个，比如一个旋转门$R_{\theta }$；我们希望寻找一个有限的量子通用门，但是有限的通用量子门只能表达可数无穷多个酉变换，也就无法准确的表达所有的酉变换，因此介绍近似通用门的概念(Approximate-universal gates)：

一个门集合G称为近似通用门(Approximate-universal gates)，如果对于任意酉变换$U$，任意$\epsilon >0$，我们都可以用G中的门近似一个酉变换$U^{\prime }$，使得$|?v|U|w???v|U^{\prime }|w?|<\epsilon$；

定理 Shi (2002): { CNOT , R θ = π 8 , S } \{\text{CNOT}, R_{\theta=\frac{\pi}{8}},S\} {CNOT,Rθ=8π??,S}和 { toffoli/CCNOT,?H,? S } \{\text{toffoli/CCNOT, H, }S\} {toffoli/CCNOT,?H,?S}是近似通用门

另外，如果你随便写一个2-qubit门，那有百分百的概率这是个近似通用门，所以其实不通用的门才是较少的。

4 编码通用门 (Encoded-universal gates)

编码通用门 (Encoded-universal gates)是更为放松的定义，即我们可以用编码通用门来有效率的进行任意量子计算；比如，虽然对于实数门，我们只能产生实数酉矩阵，但是可以证明，对于任意n-qubit复数量子电路，可以用一个(n+1)-qubit的实数量子电路来模拟。

定理: { CNOT , R θ = π 8 } \{\text{CNOT}, R_{\theta=\frac{\pi}{8}}\} {CNOT,Rθ=8π??}, { Toffoli/CCNOT,?H } \{\text{Toffoli/CCNOT, H}\} {Toffoli/CCNOT,?H}是编码通用门

5 非通用门 (Gates that are not universal)

有哪些门，连编码通用门都不是呢？

三种非通用门

• 1-qubit门，比如 { H , R θ = π 8 … ? } + qubits?swaps?only \{\text{H}, R_{\theta=\frac{\pi}{8}}\dots\}+\text{qubits swaps only} {H,Rθ=8π??…}+qubits?swaps?only；这个好理解，仅对一个qubit操作都无法产生纠缠(entanglement)，所以不通用；
• Classical门，比如 { NOT,?CNOT,?Toffoli,?Fredkin … ? } + diagonal?gates?only \{\text{NOT, CNOT, Toffoli, Fredkin}\dots\}+\text{diagonal gates only} {NOT,?CNOT,?Toffoli,?Fredkin…}+diagonal?gates?only，经典门和对角酉矩阵，都无法对叠加项(superposition)产生影响；
• Stabilizer门， { CNOT,?H,? S } \{\text{CNOT, H, }S\} {CNOT,?H,?S}，这里有个定理Gottesman & Knill (1996)说仅由Stabilizer门组成的电路可以由经典计算机在多项式时间内模拟，即只能产生离散的量子态，这种电路可以做teleportation，做CHSH游戏，但是就不能进行任意量子计算；不过后面在量子纠错会进一步介绍；

Open problem

是否所有的非通用门都是上述三种或其结合(Conjugate)呢？

这个问题现在还没被解决，但是可以知道的是，量子通用门是很容易得到的。

Universal gates, Quizzes

回答下面哪些不是通用门(近似通用门)

• { CNOT,?All?single?qubit?gates } \{\text{CNOT, All single qubit gates}\} {CNOT,?All?single?qubit?gates}，是严格通用门
• { Toffoli,?Hadamard } \{\text{Toffoli, Hadamard}\} {Toffoli,?Hadamard}, 不是通用门，因为没有虚数
• { Toffoli,?S } \{\text{Toffoli, S}\} {Toffoli,?S}，不是通用门，因为Toffoli是经典门，S是对角门，无法创建叠加
• { Toffoli,?S,?Hadamard } \{\text{Toffoli, S, Hadamard}\} {Toffoli,?S,?Hadamard}，是通用门，包括了Stabilizer门 { CNOT,?H,?S } \{\text{CNOT, H, S}\} {CNOT,?H,?S}和不是Stabilizer门的Toffoli
• { Hadamard,?S,?Controlled?Z } \{\text{Hadamard, S, Controlled Z}\} {Hadamard,?S,?Controlled?Z}，不是通用门，相当于Stabilizer门 { CNOT,?H,?S } \{\text{CNOT, H, S}\} {CNOT,?H,?S}，因为Controlled Z就是S的平方
• { Controlled?H,?Controlled?S,?NOT } \{\text{Controlled H, Controlled S, NOT}\} {Controlled?H,?Controlled?S,?NOT}，是通用门，包括了Stabilizer门 { CNOT,?H,?S } \{\text{CNOT, H, S}\} {CNOT,?H,?S}

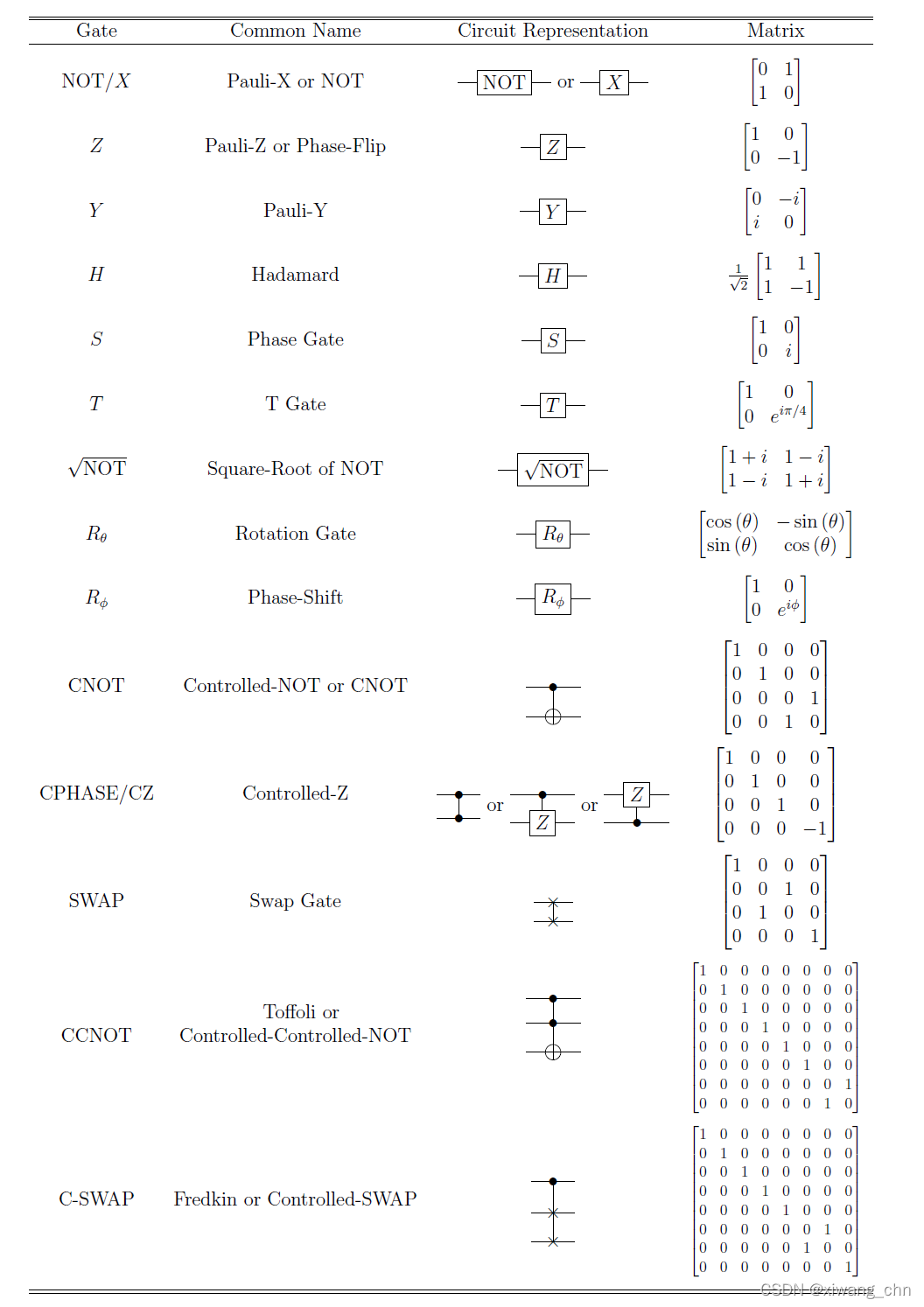
附录 常用门

2022深度学习开发者峰会

5月20日13:00让我们相聚云端，共襄盛会！