一、基本概念

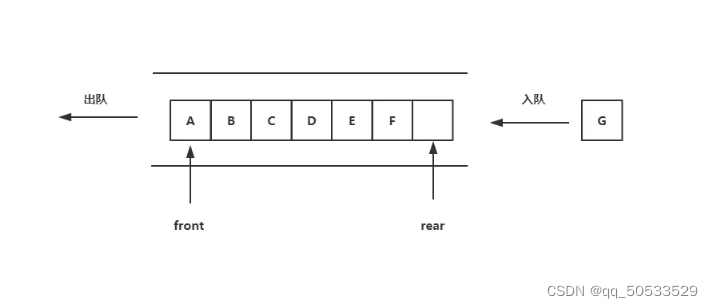
队列是一种只允许在表的一端进行操作的线性表，队列的插入称为入队，队列的删除称为出队；允许入队的一端称为队尾，允许出队的一端称为队头；不含任何元素的队列称为空队列；队列也称为先入先出线性表。本文主要介绍顺序队列和链式栈。

二、基本操作

创建队列
删除队列
判断队列是否为空
在队尾插入一个元素
取队头元素的值
队头元素出队
输出队列

三、队列的顺序表示及实现

3.1 表示

采用顺序存储结构的队列称为顺序队列，顺序队列通常用一个一维数组来存放队列中的数据元素。此外，还需要设置两个整型变量front和rear，分别指示队头和队尾，称为头指针和尾指针，front始终指向队头元素，rear始终指向队尾元素。
队列元素的入队和出队是最基本操作，顺序队列入队时，将新元素插入rear所指位置，再将rear的值加一；出队时，删除front所指位置的元素后，再将front哦值**+1**，并返回被删元素。
队列满时，再入队则产生上溢，队列为空再出队则产生下溢。
链式队列是仅在表头删除节点和仅在表尾插入节点的单链表，因为需要在表头进行删除操作和在表尾进行插入操作，所以需要front和rear指针，一个链式队列就可以由front指针和rear指针唯一确定。

3.2 问题分析与避免

由于队列经常做插入删除，front和rear会随着操作的深入而发生变化。如下图，当再进行插入，系统会误以为队列已满，造成空间浪费。

为避免出现假上溢问题，充分利用队列空间，可以将顺序队列存储空间的最后一个位置和第一个位置逻辑上链接到一起，这样的队列叫做循环队列。假设队列能够容纳MaxSize个元素，逻辑上的循环是通过头、尾指针的**+1**操作来实现的，再对其进行MaxSize求模运算，即可得出相应的指针位置，保证队列指针位置不发生错误位置索引。

front = (front+1) % MaxSize;
rear = (rear+1) % MaxSize;

如上情形，当还有新元素入队，由于rear指向0，能够进行入队，解决了假上溢问题。当然，仅根据front和rear，无法判断队列是满还是空，因为这两种状态是一样的。要解决这个问题有两种方法：

约定少用一个元素空间，入队前如果关系(rear+1)%(MaxSize-1)==front，就认为队列是满，再插入就会发生溢出，这种方法，rear指针始终指向那个空闲的元素空间。
使用一个计数器size记录当前队列长度，如果size=0，且front==rear，则当前是空队列，可以进行入队操作，否则，如果队列满的话就不能进行入队操作。

3.3 队列实现

使用C++语言实现的顺序队列和链式队列的实现如下

//顺序队列
#include<iostream>
using namespace std;

template<class T>
class LinearQueue{
	public:
		LinearQueue(int LQMaxSize);
		~LinearQueue();
		bool IsEmpty();
		bool IsFull();
		bool Insert(const T& x);
		bool GetElement(T& x);
		bool Delete(T& x);
		void Output(ostream& out) const;
		
	private:
		int size;
		int MaxSize;
		int front,rear;
		T *element;
};

template<class T>
LinearQueue<T>::LinearQueue(int LQMaxSize){
	MaxSize=LQMaxSize;
	element=new T[MaxSize];
	size=0;
	front=0;
	rear=0;
}
template<class T>
LinearQueue<T>::~LinearQueue(){
	delete []element;
}
template<class T>
bool LinearQueue<T>::IsEmpty(){
	return size==0;
}
template<class T>
bool LinearQueue<T>::IsFull(){
	return size==MaxSize;
}
template<class T>
bool LinearQueue<T>::Insert(const T& x){
	if(IsFull()){
		return false;
	}
	else{
		element[rear]=x;
		rear=(rear+1)%(MaxSize);
		size++;
		return true;
	}
}
template<class T>
bool LinearQueue<T>::GetElement(T& x){
	if(IsEmpty()){
		return false;
	}
	else{
		x=element[front];
		return true;
	}
}
template<class T>
bool LinearQueue<T>::Delete(T& x){
	if(IsEmpty()){
		return false;
	}
	else{
		x=element[front];
		front=(front+1)%(MaxSize);
		size--;
		return true;
	}
}
template<class T>
void LinearQueue<T>::Output(ostream& out) const{
	int index;
	index=front;
	for(int i=0;i<size;i++){
		out<<element[index]<<endl;
		index=(index+1)%MaxSize;
	}
}
template<class T>
ostream& operator<<(ostream& out,LinearQueue<T>& x){
	x.Output(out);
	return out;
}

void PrintSpace(int n,int k){
	for(int i=1;i<=n-k;i++){
		cout<<' ';
	}
}
void YangHui(int n){
	LinearQueue<int> Q(n+2);
	int x,y;
	PrintSpace(n,1);
	cout<<'1'<<endl;
	Q.Insert(0);
	Q.Insert(1);
	Q.Insert(1);
	for(int i=2;i<=n;i++){
		Q.Insert(0);
		PrintSpace(n,i);
		do{
			Q.Delete(x);
			Q.GetElement(y);
			if(y){
				cout<<y<<' ';
			}
			else{
				cout<<endl;
			}
			Q.Insert(x+y);
		}while(y);
	}
	cout<<endl;
}
int main(){
	YangHui(6);
	return 0;
}

//链式队列
#include<iostream>
using namespace std;

template<class T>
class LinkQueue;

template<class T>
class LinkNode{
	friend class LinkQueue<T>;
	
	public:
		LinkNode(){
			next=NULL;
		}
	private:
		T data;
		LinkNode<T> *next;
};

template<class T>
class LinkQueue{
	public:
		LinkQueue();
		~LinkQueue();
		bool IsEmpty();
		bool Insert(const T& x);
		bool GetElement(T& x);
		bool Delete(T& x);
		void Output(ostream& out) const;
	private:
		int size;
		LinkNode<T> *front,*rear;
};
template<class T>
LinkQueue<T>::LinkQueue(){
	front=NULL;
	rear=NULL;
	size=0;
}
template<class T>
LinkQueue<T>::~LinkQueue(){
	T x;
	while(front!=NULL){
		Delete(x);
	}
}
template<class T>
bool LinkQueue<T>::IsEmpty(){
	return size==0;
}
template<class T>
bool LinkQueue<T>::Insert(const T& x){
	LinkNode<T> *p=new LinkNode<T>;
	if(p==NULL){
		return false;
	}
	else{
		p->data=x;
		if(front==NULL){
			rear=p;
			front=p;
		}
		else{
			rear->next=p;
			rear=p;
		}
		size++;
		return true;
	}
}
template<class T>
bool LinkQueue<T>::GetElement(T& x){
	if(IsEmpty()){
		return false;
	}
	else{
		x=front->data;
		return true;
	}
}
template<class T>
bool LinkQueue<T>::Delete(T& x){
	LinkNode<T> *p;
	if(IsEmpty()){
		return false;
	}
	else{
		p=front;
		x=front->data;
		front=front->next;
		delete p;
		size--;
		return true;
	}
}
template<class T>
void LinkQueue<T>::Output(ostream& out) const{
	LinkNode<T> *p;
	p=front;
	for(int i=0;i<size;i++){
		out<<p->data<<endl;
		p=p->next;
	}
}
template<class T>
ostream& operator<<(ostream& out,LinkQueue<T> x){
	x.Output(out);
	return out;
}

void printspace(int n,int k){
	for(int i=1;i<=n-k;i++){
		cout<<' ';
	}
}
void yanghui(int n){
	LinkQueue<int> Q;
	int x,y;
	printspace(n,1);
	cout<<"1"<<endl;
	Q.Insert(0);
	Q.Insert(1);
	Q.Insert(1);
	for(int i=2;i<=n;i++){
		Q.Insert(0);
		printspace(n,i);
		do{
			Q.Delete(x);
			Q.GetElement(y);
			if(y){
				cout<<y<<' ';
			}
			else{
				cout<<endl;
			}
			Q.Insert(x+y);
		}while(y);
	}
	cout<<endl;
}
int main(){
	yanghui(6);
	
	return 0;
}