原题链接:zxbsmk爱查错 - 洛谷
?
?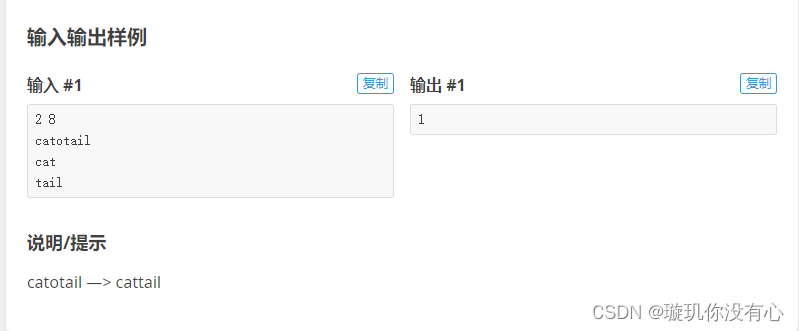 ?
?
思路:
求的是最少需要剔除的字母数,按照dp的思想:?
f[i]:字符串从1到i变成合法句子最少需要剔除的字母数
如果字符串长度是n,有m个单词,那么对于i,每次都从后往前与每一个单词进行匹配,并且找到与这个单词最近匹配完的位置(如果能匹配完就可以转移,不能匹配就转移不了),并进行状态转移。
注意:1)先考虑把s[i]删掉的情况,f[i] = f[i - 1] + 1;
? ? ? ? ? ?2)然后再考虑与每个单词一一配对的情况:如果这个单词的末尾与s[i]不能匹配就直接过,因为s[i]不能匹配,相当于这一位s[i]就得删掉,即f[i]? = f[i - 1] + 1;如果能配对,找到从后往前配对完的位子,进行状态转移。
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
#define PII pair<int,int>
#define rep(i, n) for (int i = 1; i <= (n); ++i)
#define rrep(i, n) for(int i = n; i >= 1; ++i)
using namespace std;
const double pi = acos(-1.0);
const int N = 310;
const int M = 610;
int f[N], len[M];
char a[M][27];
char s[N];
int main()
{
int m, n;
scanf("%d %d", &m, &n);
scanf("%s", s + 1);
rep(i, m) scanf("%s", a[i] + 1), len[i] = strlen(a[i] + 1);
memset(f, 0x3f, sizeof f);
f[0] = 0;
for(int i = 1; i <= n; i++)
{
f[i] = f[i - 1] + 1;
for(int j = 1; j <= m; j++)
{
if(a[j][len[j]] != s[i]) continue;
int l = i, r = len[j];
while(l > 0 && r > 0)
{
if(a[j][r] == s[l]) r--, l--;
else l--;
}
if(r == 0) f[i] = min(f[i], f[l] + i - l - len[j]);
}
}
printf("%d", f[n]);
return 0;
}
?

