| 每日一题做题记录,参考官方和三叶的题解 |
题目要求

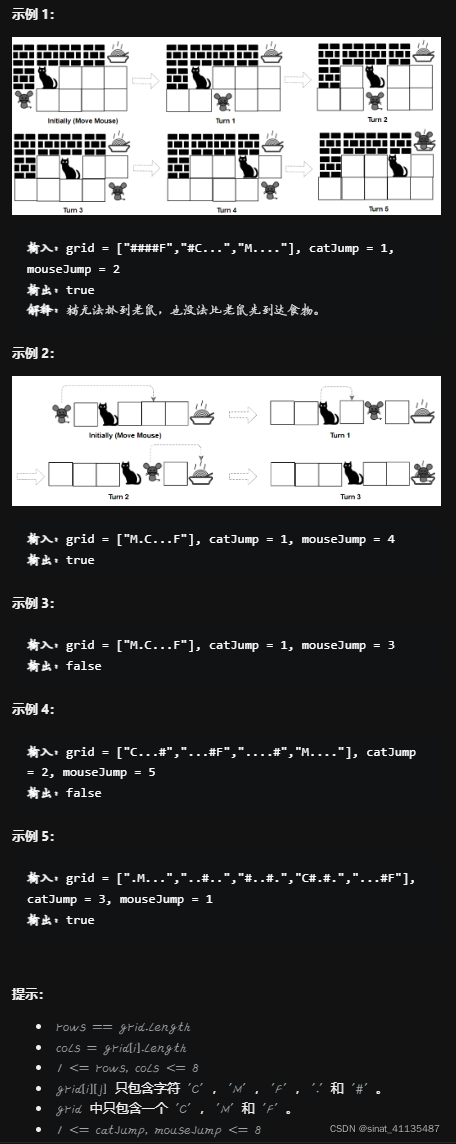
【看到标题里的II就意识到了事情的不对】
思路一:博弈论DP
Java
class Solution {
static int S = 8 * 8 * 8 * 8, th = 1000;
static int[][] f = new int[S][th]; // mouse置0, cat置1
String[] g;
int gx, gy, cj, mj, fx, fy; // 边界,最大步数,食物
int[][] dirs = new int[][]{{1,0}, {-1,0}, {0,1}, {0,-1}}; // 上下左右
int dfs(int mx, int my, int cx, int cy, int k) {
int state = (mx << 9) | (my << 6) | (cx << 3) | cy;
if(k == th - 1) // 回合上限
return f[state][k] = 1;
if(mx == cx && my == cy) // 抓到老鼠
return f[state][k] = 1;
if(mx == fx && my == fy) // 老鼠吃到
return f[state][k] = 0;
if(cx == fx && cy == fy) // 猫吃到
return f[state][k] = 1;
if(f[state][k] != -1)
return f[state][k];
if(k % 2 == 0) { // 偶数轮,老鼠移动
for(int[] di : dirs) {
for(int i = 0; i <= mj; i++) {
int nmx = mx + di[0] * i, nmy = my + di[1] * i; // 向某方向走i步
if(nmx < 0 || nmx >= gx || nmy < 0 || nmy >= gy)
break;
if(g[nmx].charAt(nmy) == '#')
break;
if(dfs(nmx, nmy, cx, cy, k + 1) == 0)
return f[state][k] = 0;
}
}
return f[state][k] = 1;
}
else { // 奇数轮,猫移动
for(int[] di : dirs) {
for(int i = 0; i <= cj; i++) {
int ncx = cx + di[0] * i, ncy = cy + di[1] * i;
if(ncx < 0 || ncx >= gx || ncy < 0 || ncy >= gy)
break;
if(g[ncx].charAt(ncy) == '#')
break;
if(dfs(mx, my, ncx, ncy, k + 1) == 1)
return f[state][k] = 1;
}
}
return f[state][k] = 0;
}
}
public boolean canMouseWin(String[] grid, int catJump, int mouseJump) {
g = grid;
gx = g.length;
gy = g[0].length();
cj = catJump;
mj = mouseJump;
int mx = 0, my = 0, cx = 0, cy = 0;
for (int i = 0; i < S; i++)
Arrays.fill(f[i], -1);
for (int i = 0; i < gx; i++) {
for (int j = 0; j < gy; j++) { // 定位猫、老鼠、食物
if (g[i].charAt(j) == 'M') {
mx = i;
my = j;
} else if (g[i].charAt(j) == 'C') {
cx = i;
cy = j;
} else if (g[i].charAt(j) == 'F') {
fx = i;
fy = j;
}
}
}
return dfs(mx, my, cx, cy, 0) == 0;
}
}
- 时间复杂度: O ( n 2 × m 2 × 1000 × 4 × L ) O(n^2\times m^2\times 1000\times 4\times L) O(n2×m2×1000×4×L),其中 m m m、 n n n分别为矩阵长宽, L L L为最长移动距离
- 空间复杂度: O ( n 2 × m 2 × 1000 ) O(n^2\times m^2\times 1000) O(n2×m2×1000)
C++
【不出所料地超时了……】
const static int S = 8 * 8 * 8 * 8, th = 1000;
class Solution {
int f[S][th]; // mouse置0, cat置1
vector<string> g;
int gx, gy, cj, mj, fx, fy; // 边界,最大步数,食物
int dirs[4][2] = {{1,0}, {-1,0}, {0,1}, {0,-1}}; // 上下左右
public:
int dfs(int mx, int my, int cx, int cy, int k) {
int state = (mx << 9) | (my << 6) | (cx << 3) | cy;
if(k == th - 1) // 回合上限
return f[state][k] = 1;
if(mx == cx && my == cy) // 抓到老鼠
return f[state][k] = 1;
if(mx == fx && my == fy) // 老鼠吃到
return f[state][k] = 0;
if(cx == fx && cy == fy) // 猫吃到
return f[state][k] = 1;
if(f[state][k] != -1)
return f[state][k];
if(k % 2 == 0) { // 偶数轮,老鼠移动
for(auto di : dirs) {
for(int i = 0; i <= mj; i++) {
int nmx = mx + di[0] * i, nmy = my + di[1] * i; // 向某方向走i步
if(nmx < 0 || nmx >= gx || nmy < 0 || nmy >= gy)
break;
if(g[nmx][nmy] == '#')
break;
if(dfs(nmx, nmy, cx, cy, k + 1) == 0)
return f[state][k] = 0;
}
}
return f[state][k] = 1;
}
else { // 奇数轮,猫移动
for(auto di : dirs) {
for(int i = 0; i <= cj; i++) {
int ncx = cx + di[0] * i, ncy = cy + di[1] * i;
if(ncx < 0 || ncx >= gx || ncy < 0 || ncy >= gy)
break;
if(g[ncx][ncy] == '#')
break;
if(dfs(mx, my, ncx, ncy, k + 1) == 1)
return f[state][k] = 1;
}
}
return f[state][k] = 0;
}
}
bool canMouseWin(vector<string>& grid, int catJump, int mouseJump) {
g = grid;
gx = g.size();
gy = g[0].size();
cj = catJump;
mj = mouseJump;
int mx = 0, my = 0, cx = 0, cy = 0;
memset(f, -1, sizeof(f));
for (int i = 0; i < gx; i++) {
for (int j = 0; j < gy; j++) { // 定位猫、老鼠、食物
if (g[i][j] == 'M') {
mx = i;
my = j;
} else if (g[i][j] == 'C') {
cx = i;
cy = j;
} else if (g[i][j] == 'F') {
fx = i;
fy = j;
}
}
}
return dfs(mx, my, cx, cy, 0) == 0;
}
};
- 时间复杂度: O ( n 2 × m 2 × 1000 × 4 × L ) O(n^2\times m^2\times 1000\times 4\times L) O(n2×m2×1000×4×L),其中 m m m、 n n n分别为矩阵长宽, L L L为最长移动距离
- 空间复杂度: O ( n 2 × m 2 × 1000 ) O(n^2\times m^2\times 1000) O(n2×m2×1000)
思路二:拓扑排序
【放着之后来搞懂】
Java
class Solution {
static final int MOUSE_TURN = 0, CAT_TURN = 1;
static final int UNKNOWN = 0, MOUSE_WIN = 1, CAT_WIN = 2;
static final int MAX_MOVES = 1000;
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int rows, cols;
String[] grid;
int catJump, mouseJump;
int food;
int[][][] degrees;
int[][][][] results;
public boolean canMouseWin(String[] grid, int catJump, int mouseJump) {
this.rows = grid.length;
this.cols = grid[0].length();
this.grid = grid;
this.catJump = catJump;
this.mouseJump = mouseJump;
int startMouse = -1, startCat = -1;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
char c = grid[i].charAt(j);
if (c == 'M') {
startMouse = getPos(i, j);
} else if (c == 'C') {
startCat = getPos(i, j);
} else if (c == 'F') {
food = getPos(i, j);
}
}
}
int total = rows * cols;
degrees = new int[total][total][2];
results = new int[total][total][2][2];
Queue<int[]> queue = new ArrayDeque<int[]>();
// 计算每个状态的度
for (int mouse = 0; mouse < total; mouse++) {
int mouseRow = mouse / cols, mouseCol = mouse % cols;
if (grid[mouseRow].charAt(mouseCol) == '#') {
continue;
}
for (int cat = 0; cat < total; cat++) {
int catRow = cat / cols, catCol = cat % cols;
if (grid[catRow].charAt(catCol) == '#') {
continue;
}
degrees[mouse][cat][MOUSE_TURN]++;
degrees[mouse][cat][CAT_TURN]++;
for (int[] dir : dirs) {
for (int row = mouseRow + dir[0], col = mouseCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row].charAt(col) != '#' && jump <= mouseJump; row += dir[0], col += dir[1], jump++) {
int nextMouse = getPos(row, col), nextCat = getPos(catRow, catCol);
degrees[nextMouse][nextCat][MOUSE_TURN]++;
}
for (int row = catRow + dir[0], col = catCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row].charAt(col) != '#' && jump <= catJump; row += dir[0], col += dir[1], jump++) {
int nextMouse = getPos(mouseRow, mouseCol), nextCat = getPos(row, col);
degrees[nextMouse][nextCat][CAT_TURN]++;
}
}
}
}
// 猫和老鼠在同一个单元格,猫获胜
for (int pos = 0; pos < total; pos++) {
int row = pos / cols, col = pos % cols;
if (grid[row].charAt(col) == '#') {
continue;
}
results[pos][pos][MOUSE_TURN][0] = CAT_WIN;
results[pos][pos][MOUSE_TURN][1] = 0;
results[pos][pos][CAT_TURN][0] = CAT_WIN;
results[pos][pos][CAT_TURN][1] = 0;
queue.offer(new int[]{pos, pos, MOUSE_TURN});
queue.offer(new int[]{pos, pos, CAT_TURN});
}
// 猫和食物在同一个单元格,猫获胜
for (int mouse = 0; mouse < total; mouse++) {
int mouseRow = mouse / cols, mouseCol = mouse % cols;
if (grid[mouseRow].charAt(mouseCol) == '#' || mouse == food) {
continue;
}
results[mouse][food][MOUSE_TURN][0] = CAT_WIN;
results[mouse][food][MOUSE_TURN][1] = 0;
results[mouse][food][CAT_TURN][0] = CAT_WIN;
results[mouse][food][CAT_TURN][1] = 0;
queue.offer(new int[]{mouse, food, MOUSE_TURN});
queue.offer(new int[]{mouse, food, CAT_TURN});
}
// 老鼠和食物在同一个单元格且猫和食物不在同一个单元格,老鼠获胜
for (int cat = 0; cat < total; cat++) {
int catRow = cat / cols, catCol = cat % cols;
if (grid[catRow].charAt(catCol) == '#' || cat == food) {
continue;
}
results[food][cat][MOUSE_TURN][0] = MOUSE_WIN;
results[food][cat][MOUSE_TURN][1] = 0;
results[food][cat][CAT_TURN][0] = MOUSE_WIN;
results[food][cat][CAT_TURN][1] = 0;
queue.offer(new int[]{food, cat, MOUSE_TURN});
queue.offer(new int[]{food, cat, CAT_TURN});
}
// 拓扑排序
while (!queue.isEmpty()) {
int[] state = queue.poll();
int mouse = state[0], cat = state[1], turn = state[2];
int result = results[mouse][cat][turn][0];
int moves = results[mouse][cat][turn][1];
List<int[]> prevStates = getPrevStates(mouse, cat, turn);
for (int[] prevState : prevStates) {
int prevMouse = prevState[0], prevCat = prevState[1], prevTurn = prevState[2];
if (results[prevMouse][prevCat][prevTurn][0] == UNKNOWN) {
boolean canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
if (canWin) {
results[prevMouse][prevCat][prevTurn][0] = result;
results[prevMouse][prevCat][prevTurn][1] = moves + 1;
queue.offer(new int[]{prevMouse, prevCat, prevTurn});
} else {
degrees[prevMouse][prevCat][prevTurn]--;
if (degrees[prevMouse][prevCat][prevTurn] == 0) {
int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
results[prevMouse][prevCat][prevTurn][0] = loseResult;
results[prevMouse][prevCat][prevTurn][1] = moves + 1;
queue.offer(new int[]{prevMouse, prevCat, prevTurn});
}
}
}
}
}
return results[startMouse][startCat][MOUSE_TURN][0] == MOUSE_WIN && results[startMouse][startCat][MOUSE_TURN][1] <= MAX_MOVES;
}
public List<int[]> getPrevStates(int mouse, int cat, int turn) {
List<int[]> prevStates = new ArrayList<int[]>();
int mouseRow = mouse / cols, mouseCol = mouse % cols;
int catRow = cat / cols, catCol = cat % cols;
int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
int maxJump = prevTurn == MOUSE_TURN ? mouseJump : catJump;
int startRow = prevTurn == MOUSE_TURN ? mouseRow : catRow;
int startCol = prevTurn == MOUSE_TURN ? mouseCol : catCol;
prevStates.add(new int[]{mouse, cat, prevTurn});
for (int[] dir : dirs) {
for (int i = startRow + dir[0], j = startCol + dir[1], jump = 1; i >= 0 && i < rows && j >= 0 && j < cols && grid[i].charAt(j) != '#' && jump <= maxJump; i += dir[0], j += dir[1], jump++) {
int prevMouseRow = prevTurn == MOUSE_TURN ? i : mouseRow;
int prevMouseCol = prevTurn == MOUSE_TURN ? j : mouseCol;
int prevCatRow = prevTurn == MOUSE_TURN ? catRow : i;
int prevCatCol = prevTurn == MOUSE_TURN ? catCol : j;
int prevMouse = getPos(prevMouseRow, prevMouseCol);
int prevCat = getPos(prevCatRow, prevCatCol);
prevStates.add(new int[]{prevMouse, prevCat, prevTurn});
}
}
return prevStates;
}
public int getPos(int row, int col) {
return row * cols + col;
}
}
- 时间复杂度: O ( n 2 × m 2 × ( n + m ) ) O(n^2\times m^2\times(n+m)) O(n2×m2×(n+m)),其中 m m m、 n n n分别为矩阵长宽。状态数是 O ( m 2 × n 2 ) O(m^2 \times n^2) O(m2×n2),对于每个状态需要 O ( m + n ) O(m+n) O(m+n)的时间计算状态值。
- 空间复杂度: O ( m 2 × n 2 ) O(m^2 \times n^2) O(m2×n2),需记录每个状态的度和结果,状态数是 O ( m 2 × n 2 ) O(m^2 \times n^2) O(m2×n2)。
C++
static const int MOUSE_TURN = 0, CAT_TURN = 1;
static const int UNKNOWN = 0, MOUSE_WIN = 1, CAT_WIN = 2;
static const int MAX_MOVES = 1000;
class Solution {
public:
vector<vector<int>> dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int rows, cols;
vector<string> grid;
int catJump, mouseJump;
int food;
int degrees[64][64][2];
int results[64][64][2][2];
bool canMouseWin(vector<string> grid, int catJump, int mouseJump) {
this->rows = grid.size();
this->cols = grid[0].size();
this->grid = grid;
this->catJump = catJump;
this->mouseJump = mouseJump;
int startMouse = -1, startCat = -1;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
char c = grid[i][j];
if (c == 'M') {
startMouse = getPos(i, j);
} else if (c == 'C') {
startCat = getPos(i, j);
} else if (c == 'F') {
food = getPos(i, j);
}
}
}
int total = rows * cols;
memset(degrees, 0, sizeof(degrees));
memset(results, 0, sizeof(results));
queue<tuple<int, int, int>> qu;
// 计算每个状态的度
for (int mouse = 0; mouse < total; mouse++) {
int mouseRow = mouse / cols, mouseCol = mouse % cols;
if (grid[mouseRow][mouseCol] == '#') {
continue;
}
for (int cat = 0; cat < total; cat++) {
int catRow = cat / cols, catCol = cat % cols;
if (grid[catRow][catCol] == '#') {
continue;
}
degrees[mouse][cat][MOUSE_TURN]++;
degrees[mouse][cat][CAT_TURN]++;
for (auto & dir : dirs) {
for (int row = mouseRow + dir[0], col = mouseCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row][col] != '#' && jump <= mouseJump; row += dir[0], col += dir[1], jump++) {
int nextMouse = getPos(row, col), nextCat = getPos(catRow, catCol);
degrees[nextMouse][nextCat][MOUSE_TURN]++;
}
for (int row = catRow + dir[0], col = catCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row][col] != '#' && jump <= catJump; row += dir[0], col += dir[1], jump++) {
int nextMouse = getPos(mouseRow, mouseCol), nextCat = getPos(row, col);
degrees[nextMouse][nextCat][CAT_TURN]++;
}
}
}
}
// 猫和老鼠在同一个单元格,猫获胜
for (int pos = 0; pos < total; pos++) {
int row = pos / cols, col = pos % cols;
if (grid[row][col] == '#') {
continue;
}
results[pos][pos][MOUSE_TURN][0] = CAT_WIN;
results[pos][pos][MOUSE_TURN][1] = 0;
results[pos][pos][CAT_TURN][0] = CAT_WIN;
results[pos][pos][CAT_TURN][1] = 0;
qu.emplace(pos, pos, MOUSE_TURN);
qu.emplace(pos, pos, CAT_TURN);
}
// 猫和食物在同一个单元格,猫获胜
for (int mouse = 0; mouse < total; mouse++) {
int mouseRow = mouse / cols, mouseCol = mouse % cols;
if (grid[mouseRow][mouseCol] == '#' || mouse == food) {
continue;
}
results[mouse][food][MOUSE_TURN][0] = CAT_WIN;
results[mouse][food][MOUSE_TURN][1] = 0;
results[mouse][food][CAT_TURN][0] = CAT_WIN;
results[mouse][food][CAT_TURN][1] = 0;
qu.emplace(mouse, food, MOUSE_TURN);
qu.emplace(mouse, food, CAT_TURN);
}
// 老鼠和食物在同一个单元格且猫和食物不在同一个单元格,老鼠获胜
for (int cat = 0; cat < total; cat++) {
int catRow = cat / cols, catCol = cat % cols;
if (grid[catRow][catCol] == '#' || cat == food) {
continue;
}
results[food][cat][MOUSE_TURN][0] = MOUSE_WIN;
results[food][cat][MOUSE_TURN][1] = 0;
results[food][cat][CAT_TURN][0] = MOUSE_WIN;
results[food][cat][CAT_TURN][1] = 0;
qu.emplace(food, cat, MOUSE_TURN);
qu.emplace(food, cat, CAT_TURN);
}
// 拓扑排序
while (!qu.empty()) {
auto [mouse, cat, turn] = qu.front();
qu.pop();
int result = results[mouse][cat][turn][0];
int moves = results[mouse][cat][turn][1];
vector<tuple<int, int, int>> prevStates = getPrevStates(mouse, cat, turn);
for (auto [prevMouse, prevCat, prevTurn] : prevStates) {
if (results[prevMouse][prevCat][prevTurn][0] == UNKNOWN) {
bool canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
if (canWin) {
results[prevMouse][prevCat][prevTurn][0] = result;
results[prevMouse][prevCat][prevTurn][1] = moves + 1;
qu.emplace(prevMouse, prevCat, prevTurn);
} else {
degrees[prevMouse][prevCat][prevTurn]--;
if (degrees[prevMouse][prevCat][prevTurn] == 0) {
int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
results[prevMouse][prevCat][prevTurn][0] = loseResult;
results[prevMouse][prevCat][prevTurn][1] = moves + 1;
qu.emplace(prevMouse, prevCat, prevTurn);
}
}
}
}
}
return results[startMouse][startCat][MOUSE_TURN][0] == MOUSE_WIN && results[startMouse][startCat][MOUSE_TURN][1] <= MAX_MOVES;
}
vector<tuple<int, int, int>> getPrevStates(int mouse, int cat, int turn) {
vector<tuple<int, int, int>> prevStates;
int mouseRow = mouse / cols, mouseCol = mouse % cols;
int catRow = cat / cols, catCol = cat % cols;
int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
int maxJump = prevTurn == MOUSE_TURN ? mouseJump : catJump;
int startRow = prevTurn == MOUSE_TURN ? mouseRow : catRow;
int startCol = prevTurn == MOUSE_TURN ? mouseCol : catCol;
prevStates.emplace_back(mouse, cat, prevTurn);
for (auto & dir : dirs) {
for (int i = startRow + dir[0], j = startCol + dir[1], jump = 1; i >= 0 && i < rows && j >= 0 && j < cols && grid[i][j] != '#' && jump <= maxJump; i += dir[0], j += dir[1], jump++) {
int prevMouseRow = prevTurn == MOUSE_TURN ? i : mouseRow;
int prevMouseCol = prevTurn == MOUSE_TURN ? j : mouseCol;
int prevCatRow = prevTurn == MOUSE_TURN ? catRow : i;
int prevCatCol = prevTurn == MOUSE_TURN ? catCol : j;
int prevMouse = getPos(prevMouseRow, prevMouseCol);
int prevCat = getPos(prevCatRow, prevCatCol);
prevStates.emplace_back(prevMouse, prevCat, prevTurn);
}
}
return prevStates;
}
int getPos(int row, int col) {
return row * cols + col;
}
};
- 时间复杂度: O ( n 2 × m 2 × ( n + m ) ) O(n^2\times m^2\times(n+m)) O(n2×m2×(n+m)),其中 m m m、 n n n分别为矩阵长宽。状态数是 O ( m 2 × n 2 ) O(m^2 \times n^2) O(m2×n2),对于每个状态需要 O ( m + n ) O(m+n) O(m+n)的时间计算状态值。
- 空间复杂度: O ( m 2 × n 2 ) O(m^2 \times n^2) O(m2×n2),需记录每个状态的度和结果,状态数是 O ( m 2 × n 2 ) O(m^2 \times n^2) O(m2×n2)。
总结
就勉强搞懂个博弈论DP,剩下的拓扑排序cv了,感觉现在的level还不至于来磨这种题……
【满课还有一场考试,一道困难忙哭了呀】
| 欢迎指正与讨论! |
