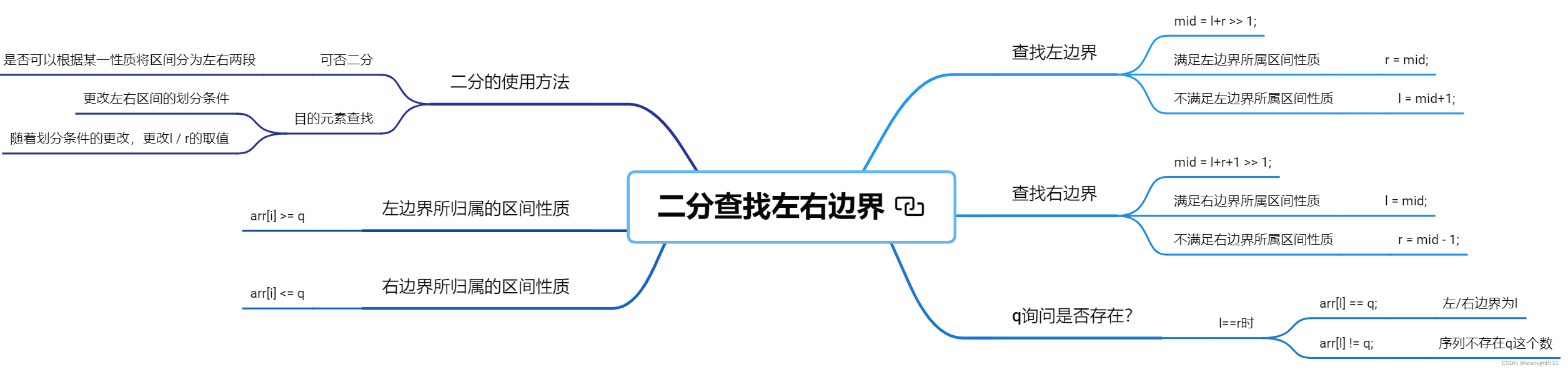
整数二分求边界
食用指南:
对该算法程序编写以及踩坑点很熟悉的同学可以直接跳转到代码模板查看完整代码
只有基础算法的题目会有关于该算法的原理,实现步骤,代码注意点,代码模板,代码误区的讲解
非基础算法的题目只有题目分析,代码实现,代码误区
题目描述:
-
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0 开始计数)。
如果数组中不存在该元素,则返回 -1。
输入格式
第一行包含整数 n 和 q,表示数组长度和询问个数。第二行包含 n 个整数(均在 1~10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1 -
题目来源:https://www.acwing.com/problem/content/791/
题目分析:
- 序列具有“近似单调性”即非递减,且是整数序列,貌似可以二分
- 被查询数q在本题中出现不只一次,且询问的是q出现的左端点和右端点
- 可能有的同学只做过q只出现一次且序列为单调序列的二分题目,觉得这个题不能二分,其实是对二分查找认识不全面,下面介绍整数二分
算法原理:
整数二分的适用范围:
- 表面二分:单调序列
- 本质二分:可以按照某一性质将序列分为左右两段,如之前的快速选择算法
- 划分区间的判别条件不同,搭配使用选择性舍弃左或右半个区间,我们可以查找到不同的边界
回顾经典单调序列二分模型:
- 单调序列中没有重复元素,q仅出现了一次,求q出现的位置:
- 试探法:每次试探q在中点mid的左边还是右边,决定舍弃左边一半或者右边一半
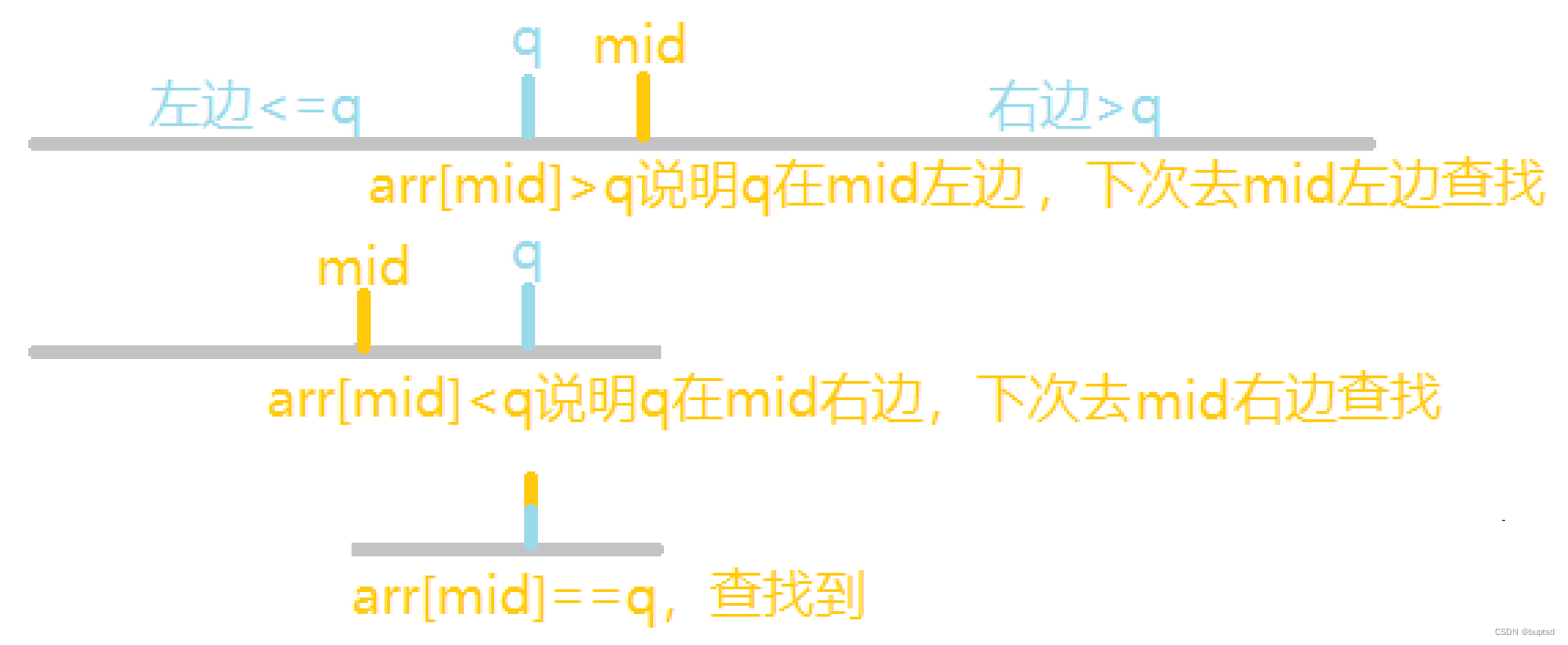
求q:q将区间划分3部分,左边<q & 右边>q & mid==q。所以严格说是三分,但是每次我们只舍弃了一半区间,也可以说是二分
非递减序列求边界二分模型:
- 划分区间的判别条件不同,搭配选择性舍弃左右半个区间,我们可以查找到不同的边界
- 求左边界:
左边界将区间划分为两部分:左边<q & 右边>=q
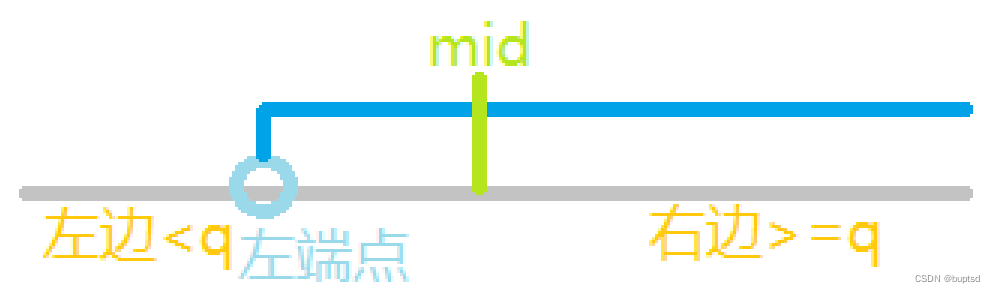
- arr[mid]>=q时,左端点在mid左侧,舍弃mid右侧,r = mid
- arr[mid]<q时,左端点在mid右侧,舍弃mid左侧,l = mid+1
- 注意此时的边界arr[mid]归属:
arr[mid]>=q,mid可能是边界,下一次继续查找mid,所以r=mid
arr[mid]<q,则mid绝对不可能是边界,下一次不必查找mid了,所以l = mid+1 - l == r时,arr[l] == q 则说明序列中有q,左边界就是l;反之arr[l] != q,则说明序列中无q,查找到的是序列中最近似q的数,输出-1
- 求右边界:
右边界将区间划分为两部分:左边<=q & 右边>q
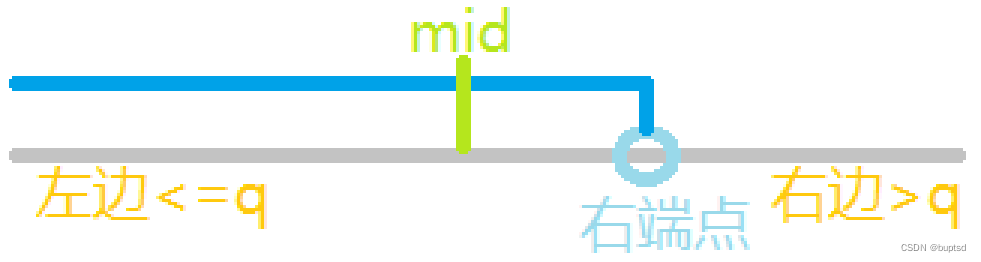
- arr[mid] > q时,右端点在mid左侧,舍弃mid右侧,且arr[mid]必定不是端点,下一次不必查找mid,r = mid -1
- arr[mid] <= q时,右端点在mid右侧,舍弃mid左侧,且arr[mid]可能是端点,下一次需要考察mid,所以l = mid
- l == r时,arr[l] == q 则说明序列中有q,右边界就是l;反之arr[l] != q,则说明序列中无q,查找到的是序列中最近似q的数,输出-1
写作步骤:
三步走:
- 选取中点:
找左端点需要mid = l+r >> 1
找右端点需要mid = l + r + 1 >> 1
目的和快排一样为了防止死循环 - 取舍区间:
找左端点:
mid满足左端点性质>=q,则舍弃mid右,r = mid;
mid不满足左端点性质<q,则舍弃mid左,l = mid + 1;
找右端点:mid满足右端点性质<=q,则舍弃mid左,l = mif;
mid不满足右端点性质>q,则舍弃mid右, r = mid - 1; - 循环迭代,直到l == r,判断arr[l] == q?
核心算法:
- 左右边界所属区间的性质判断
- mid的取值偏左或右,防止死迭代
- l & r的取舍:
中点是否满足边界所属区间的性质
当寻找的是区间左边界:
? 满足: r = mid
? 不满足:l = mid+1
当寻找的是区间右边界:
? 满足:l = mid
? 不满足:r = mid-1
- 🌟关键的部分:mid的取值 & l r的替换
- 🌟发挥作用的部分:r / l 的替换
- 🌟避免死循环的部分:mid取值
代码注意:
- 左边界所属区间的性质:左端点右侧>=q
右边界所属区间的性质:右端点左侧<=q - 寻找左边界时, mid = (l+r)>>1; 防止死迭代
寻找右边界时,mid = (l+r+1)>>1; 防止死迭代 - 寻找左边界时,从右向左查找q,mid满足左端点性质则r = mid
寻找右边界时,从左向右查找q,mid满足右端点性质则l = mid - 寻找左边界时,
满足则区间划分为:[l , mid]
不满足则区间划分为: [mid+1 , r]
寻找右边界时,
满足则区间划分为:[mid , r]
不满足则区间划分为 :[l , mid-1]
代码模板:
寻找左边界:
bool check(mid){
return arr[mid] >= q;
}
while(l < r){
int mid = (l+r) >> 1;
//check()函数就是判断mid是否满足左边界性质:>=q
if (check(mid)) r = mid;
else l = mid+1;
}
寻找右边界:
bool check(mid){
return arr[mid] <= q;
}
while(l < r){
int mid = (l+r+1)>>1;
//check()函数就是判断mid是否满足右边界性质:<=q
if (check(mid)) l = mid;
else r = mid-1;
}
本题题解:
#include <iostream>
using namespace std;
const int N = 100010;
int n, q;
int arr[N];
int bsearch_left(int x){
int l = 0, r = n-1;
while(l < r){
int mid = (l+r)>>1;
if(arr[mid] >= x) r = mid;
else l = mid+1;
}
if (arr[l] == x) return l;
else return -1;
}
int bsearch_right(int x){
int l = 0, r = n-1;
while(l < r){
int mid = (l+r+1) >> 1;
if(arr[mid] <= x) l = mid;
else r = mid-1;
}
if(arr[l] == x) return l;
else return -1;
}
int main(){
cin >>n >>q;
for(int i=0; i<n; i++) cin>>arr[i];
for(int i=0; i<q; i++){
int x = 0;
cin >>x;
cout<<bsearch_left(x)<<" "<<bsearch_right(x)<<endl;
}
return 0;
}
代码误区:
!!!本题给的有序区间,不然需要自己sort()!!!
mid取值问题:
为什么寻找左边界mid = (l+r)>>1;
但是寻找右边界mid = (l+r+1)>>1?
解答:
当l 和 r 距离很近,距离为1时:
l = r-1
如果将要替换l 的 mid = (l+r)>>1 由于向下取整,等于l,相当于区间没变,还是[l,r],陷入死循环
如果将要替换r 的 mid = (l+r)>>1 由于向下取整,等于1,此时区间变化,是[l,l],即找到了目标点
总结:由于>>1 或者 /2 的地板除法,导致r和l相距为1时,mid 总是等于l,此时对原本要替换l的情况(找右边界)无效,陷入死循环
mid替换问题:
-
寻找左边界
满足条件,替换r,不必防止地板除,mid = (l+r)>>1; -
寻找右边界
满足条件,替换l,防止地板除,令mid = (l+r+1)>>1;
mid取舍问题:
-
寻找左边界
mid满足条件:r = mid [l , mid]
mid可能是边界,可能是边界右,所以下一次查找要查mid
mid不满足条件:l = mid+1 [mid+1 , r]]
mid不可能是边界,下一次查找不用查mid了 -
寻找右边界
mid满足条件:l = mid [mid , r]
mid 可能是边界,下一次查找要查mid
mid不满足条件:r = mid-1 [l , mid-1
mid 不可能是边界,下一次查找不用查mid
本篇感想:
- 感觉写的挺冗余,其实一句话概括一下就是查找左/右边界,mid取值就靠左/右,mid满足左/右边界性质则下一次查找r/l = mid
- 思维导图 以及 算法原理的例子写的比较好,只看这两部分应该也能理解整数二分求边界问题
- 当然,能够理解《代码误区》中的三个问题,说明你确实是完全理解了
- 看完本篇博客,恭喜已登《练气境-初期》

距离登仙境不远了,加油
