1.实验目的
掌握模拟退火算法解决旅行商问题的方法。
2.实验环境
Matlab
3.实验内容
使用模拟退火算法解决14个城市的TSP问题,使得从一个城市出发,遍历所有城市回到起点的路线最短。已知14个城市的位置为
X=[16.4700 ??96.1000
???16.4700 ??94.4400
???20.0900 ??92.5400
???22.3900 ??93.3700
???25.2300 ??97.2400
???22.0000 ??96.0500
???20.4700 ??97.0200
???17.2000 ??96.2900
???16.3000 ??97.3800
???14.0500 ??98.1200
???16.5300 ??97.3800
???21.5200 ??95.5900
???19.4100 ??97.1300
???20.0900 ??92.5500];
4.实验过程
初始参数:T0(初始温度) T_end(结束温度) L(链长) alpha(降温速率) S1(初始解)
1.计算任意两点间的距离矩阵
2.生成新解
3.根据Metropolis准则判断是否接受新解
4.继续迭代,直到达到了迭代次数
5.降温
6.重复上面的2~5,直到温度降到最低
定义的函数:
1.根据每个城市的坐标计算任意距离矩阵函数Distence.m
2.绘制路线图Drawpath.m
3.计算一个解的距离的函数CalDist.m
4.生成新解的函数NewSolution.m
5.Metropolis准则函数,传入参数为(df,T_now),返回0或1。1代表接受新解,Metropolis.m
6.输出解的函数Disp.m
总体思路:给定初始温度,温度大于最低温度的时候,代表计算还在继续。每迭代一次,温度以指数规律减少。每次迭代时,指定链长L是操作的最大次数,我们每次迭代一共生成L次新解
Diatance.m (生成距离矩阵,距离矩阵的第i行第j列代表第i个城市与第j个城市之间的距离)
function y=Distance(Label)
% Label是城市1~N的坐标
[Num,~]=size(Label);
y=zeros(Num,Num);%坐标矩阵初始化
for i=1:Num
for j=1:Num
y(i,j)=sqrt((Label(i,1)-Label(j,1))^2+(Label(i,2)-Label(j,2))^2);
end
end
Metropolis.m (Metropolis准则)
function L=Metropolis(df,T)
if df<0 %新解比当前解小的时候,一定接受新解
L=1;
else
r=rand(1);
if r<exp(-df/T) %新解大于当前解的时候,概率接受新解,接受概率取决于当前温度和新解与旧解之差
L=1;
else
L=0;
end
end
CalDist.m?(根据当前解和城市的距离矩阵,生成这条路线的距离总和)
function sum=CalDist(s,Matrix)% s是当前解,Matrix是距离矩阵
[~,Num]=size(s);
sum=0;
for i=1:Num-1
sum=sum+Matrix(s(i),s(i+1));
end
sum=sum+Matrix(Num,1);
NewSolution.m?(用随机交换两个城市的方法生成新解)
function s1=NewSolution(s)
[~,Num]=size(s);
R=round(rand(1,2)*(Num-1)+1);
s1=s;
s1(R(1))=s(R(2));
s1(R(2))=s(R(1));
Drawpath.m(已知序列和各个城市的坐标矩阵,绘制路线图)?
function Drawpath(S,coordinate)
[~,Num]=size(S);
ChormMatrix=zeros(2,Num+1);
for i=1:Num
ChormMatrix(1,i)=coordinate(S(i),1);
ChormMatrix(2,i)=coordinate(S(i),2);
end
ChormMatrix(1,Num+1)=ChormMatrix(1,1);
ChormMatrix(2,Num+1)=ChormMatrix(2,1);
figure
hold on
plot(ChormMatrix(1,:),ChormMatrix(2,:))
Disp.m?(已知一个序列,输出路线)
function Disp(S)
[~,Num]=size(S);
p=num2str(S(1));
for i=2:Num-1
p=[p,'->',num2str(S(i))];
end
disp(p)
TSP.m(主程序)
%模型的初始参数可以随时修改,L是链长,代表同一个温度下迭代的次数
X=[16.4700 96.1000
16.4700 94.4400
20.0900 92.5400
22.3900 93.3700
25.2300 97.2400
22.0000 96.0500
20.4700 97.0200
17.2000 96.2900
16.3000 97.3800
14.0500 98.1200
16.5300 97.3800
21.5200 95.5900
19.4100 97.1300
20.0900 92.5500];
%citydataset代表当前的(N*2)数据集
citydataset=X;
%模型的初始参数可以随时修改,L是链长,代表同一个温度下迭代的次数
S1=randperm(Num);%S1代表目前的解
DistMatrix=Distance(citydataset);%距离矩阵,第i行第j列是城市i到城市j的距离
disp(['初始路线的长度是:',num2str(CalDist(S1,DistMatrix))])
T_now=T0;
Drawpath(S1,citydataset)
%Tset=T_now;
Tset=1;p=1;
Calset=CalDist(S1,DistMatrix);
while T_now>T_end
k=1;
while k<=L
S_new=NewSolution(S1);
df=CalDist(S_new,DistMatrix)-CalDist(S1,DistMatrix);
if Metropolis(df,T_now)==1 %接受新解
S1=S_new;
end
k=k+1;
end
T_now=T_now*alpha;
%Tset=[Tset,T_now];
Tset=[Tset,p];p=p+1;
cal=CalDist(S1,DistMatrix);
Calset=[Calset,cal];
end
figure
plot(Tset,Calset)
xlabel('迭代次数')
ylabel('当前的总路线长度')
Drawpath(S1,citydataset)
disp('最终的路线是:')
Disp([S1])
disp(['最终路线的长度是:',num2str(CalDist(S1,DistMatrix))])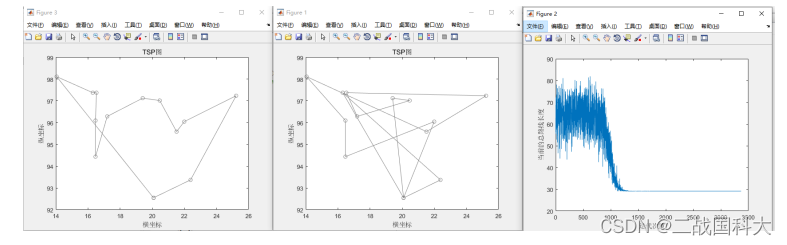
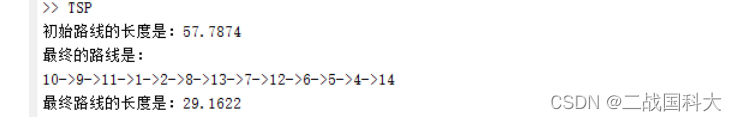 ?
?
?
- 实验总结
函数?模拟退火算法(Simulated Annealing, SA)的思想借鉴于固体的退火原理,当固体的温度很高的时候,内能比较大,固体的内部粒子处于快速无序运动,当温度慢慢下降的过程当中,固体的内能减少,粒子的慢慢趋于有序,最终,当固体处于常温时,内能达到最小,此时,粒子最为稳定。?
从上面的过程我们可以看出,模拟退火算法是一种随机算法,它有一定的概率能求得全局最优解,但不一定。其目标是要找到函数的最大值,若初始化时,初始点的位置在A处,则会寻找到附近的局部最大值B点处,因为B点出是一个局部最大值点,故对于通常算法来说,好比梯度降低法,该算法没法跳出局部最优值。
