第一题
*选择题严禁使用程序验证
设s='Hi LanQiao',运行以下哪个选项代码可以输出“LanQiao”子串(A)。
A、print(s[-7:])?? ?B、print(s[-6:-1])?? ?C、print(s[-7:0])?? ?D、print(s[-7:-1])
第二题
*选择题严禁使用程序验证
已知a=2021.0529,运行以下哪个选项代码可以输出“2021.05”(B)。
A、print('{.2f}'.format(a))?? ?B、print('{:.2f}'.format(a))
C、print('{.2}'.format(a))?? ?D、print('{2}'.format(a))
第三题
*选择题严禁使用程序验证
已知pi=3.1415926,运行print(round(pi),round(pi,2))语句,输出的结果是(A)。
A、3 3.14 ??? ?B、2 4?? ? ? C、3 6.18 ??? ?D、3.14 3
第四题
*选择题严禁使用程序验证
运行以下程序,输出的结果是(D)。
d={'Beijing':'China','Washington':'America','Ottawat':'Canadian'}
print(max(d),min(d))
A、Washington Ottawa?? ?B、Canadian China
C、America China?? ??? ?D、Washington Beijing
第五题
*选择题严禁使用程序验证
如果p=ord('b'),运行print(p,chr((p+3)%26+p))语句,输出的结果是(C)。
A、66 D?? ?B、66 S?? ?C、98 y?? ?D、98 e
第一题
编程实现:
给定N个数字(包含整数和小数),找到N个数中最大的数字。
输入描述:输入N个数字(N>2),且N个数字之间以英文逗号隔开
输出描述:输出N个数字中最大的数字
样例输入:4,8,2
样例输出:8
print(max(list(map(eval,input().split(',')))))第二题
提示信息:
质数:是一个大于1的自然数,且除了1和它本身外,不能被其他自然数整除的数。最小的质数是2,1不是质数。
合数:一个正整数,如果除1和它本身以外,还能被其他正整数整除,叫合数。如6是合数,除了1和6以外,还能被2和3整除。
分解质因数:每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,把一个合数用质因数相乘的形式表示出来,叫做分解质因数(分解质因数只针对合数)。如合数12=2×2×3。
分解质因数的方法是先用这个合数的最小质因数去除这个合数,结果若是一个质数就不再除下去;若是一个合数就继续按原来的方法从最小质因数除起,直至最后除得的结果是一个质数。
例如: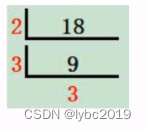
合数18分解质因数,首先用最小质因数2去除,除后结果为合数9,继续用最小质因数3去除,除后结果为质数3,就不再除下去。所以18的质因数为2、3、3,故质因数的个数为3;
编程实现:
给定一个合数N,将N分解质因数后,输出其质因数个数。
输入描述:输入一个合数N
输出描述:将N分解质因数后,输出质因数个数
样例输入:18
样例输出:3
n=int(input())
ls=[]
for i in range (2,n//2+1):
while n%i==0 and n>1 :
ls.append(i)
n//=i
if n==1:
break
print(len(ls))第三题
编程实现:
给定一个含有字母和数字的字符串,输出此字符串中最长的数字子串的长度。如:字符串“a2a22d”,最长的数字子串为22,长度为2,故输出2
字符串“1q12h567j765”,最长的数字子串为567和765,长度都为3,故输出3
输入描述:
输入一个含有字母和数字的字符串(5<字符串长度<101)
输出描述:
输出此字符串中最长的数字子串的长度
样例输入:a2a22d
样例输出:2
s=input()
ls=[]
t=0
for i in s:
if i.isdigit():
t+=1
else:
t=0
ls.append(t)
print(max(ls))第四题
提示信息:
质数:是一个大于1的自然数,且除了1和它本身外,不能被其他自然数整除的数。最小的质数是2,1不是质数。
大于2的偶数有一个特点,任意一个大于2的偶数可以由一对质数相加得到,但有的偶数不止有一对这样的质数对。
如偶数6,有一对质数相加得6,为(3,3)
如偶数14,有两对质数相加得14,分别是(3,11),(7,7)
编程实现:
给定一个大于2的偶数,在所有满足“任意一个大于2的偶数可以由两个质数相加得到”这个特点的质数对中,找出两个质数差值最小的一对,并将差值输出(差值为大数减小数的值,两个质数相等时差值为0)。
例如:偶数16,满足特点的质数对有(5,11)和(3,13),差值最小的一对是(5,11),11减5,差值为6。
输入描述:
输入一个大于2的偶数N
输出描述:
输出满足“任意一个大于2的偶数可以由两个质数相加得到”这个特点的所有质数对中,差值最小的那一对的差值
样例输入:16
样例输出:6
import math
def prim(n):
if n<2:
return False
for i in range(2,int(math.sqrt(n))+1):
if n%i==0:
return False
else :
return True
n=int(input())
for i in range(n//2,n+1):
if prim(i) and prim(n-i):
print(i-(n-i))
break第五题
编程实现:
孙悟空的金箍棒可以变高也可以变矮还可以变出多个金箍棒。
这天孙悟空无聊变出了N个长短不一金箍棒,这些金箍棒之间相互吵闹,攀比谁高。当孙悟空每次手指其中一个金箍棒时,这个金箍棒高度不变,其他的金箍棒高度都会增加1。只有当所有金箍棒高度都一样时,他们之间才不相互吵闹,也不会再增加高度,保持静止。分别给定N个金箍棒的初始高度,请你帮助孙悟空计算一下至少手指几次可以让N个金箍棒高度都一样。
例如:有3个金箍棒,初始高度分别为2,3,4。
第一次手指第三个金箍棒,第三个金箍棒高度不变,第一和第二个金箍棒高度分别增加1,变为3,4,4;第二次手指第二个金箍棒,第二个金箍棒高度不变,第一和第三个金箍棒高度分别增加1,变为4,4,5;第三次手指第三个金箍棒,第三个金箍棒高度不变,第一和第二个金箍棒高度分别增加1,变为5,5,5;这时3个金箍棒的高度都为5,手指3次后金箍棒高度一样。所以至少手指3次才能使金箍棒高度都一样。
输入描述:
输入N个非全部相等的正整数(2<N<31),且之间以英文逗号隔开,分别表示N个金箍棒的初始高度
输出描述:输出一个正整数,表示至少手指几次才能使金箍棒高度都一样
样例输入:2,3,4
样例输出:3
ls=list(map(int,input().split(',')))
n=len(ls)
ans=0
while True:
ls.sort()
if ls[0]==ls[n-1]:
break
for i in range(n-1):
ls[i]+=1
ans+=1
print(ans)第六题
编程实现:
六月一日是国际儿童节,小蓝的学校为迎接儿童节要在学校的一块正方形空地上使用不同颜色的花卉摆放图案。
为了摆放的更精准,图案更漂亮,小蓝把这块正方形空地同比例缩小将其画在纸上,并平分成100*100的方格,每个方格的坐标点为,(1,1)...(100,100),如下图: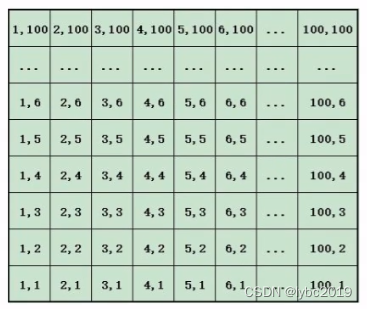
首先在指定坐标的方格内放置红色的花卉(每个方格放一盆),完成后,找出最多有多少盆红色花卉在同一条直线上。(同一直线包含同一列、同一行、同一对角线,红色花卉可以连续也可以不连续)
如:指定的坐标(2,1)、(3,2)、(5,2)、(4,3)、(3,4)、(6,5)的方格内放置红色的花卉,其中最多的红色花卉在同一条直线上的坐标点为(2,1)、(3,2)、(4,3)、(6,5),故最多有4盆红色的花卉在同一条直线上。
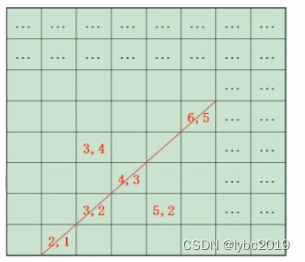
输入样例:2,1 3,2 5,2 4,3 3,4 6,5
输出样例:
#初始化读入数据
lst=input().split(' ')
ls=[]
for i in lst:
ls.append(list(map(int,i.split(','))))
m=0
# 右斜线
ls_=[]
for i in ls:
ls_.append(sum(i))
for i in ls_:
m=max(m,ls_.count(i))
#左斜线
ls_=[]
for i in ls:
ls_.append(i[0]-i[1])
for i in ls_:
m=max(m,ls_.count(i))
#行
ls_=[]
for i in ls:
ls_.append(i[0])
for i in ls_:
m=max(m,ls_.count(i))
#列
ls_=[]
for i in ls:
ls_.append(i[1])
for i in ls_:
m=max(m,ls_.count(i))
print(m)